Haplotype phasing: Existing methods and new developments (original) (raw)

. Author manuscript; available in PMC: 2012 Apr 1.

Published in final edited form as: Nat Rev Genet. 2011 Sep 16;12(10):703–714. doi: 10.1038/nrg3054

Abstract

Determination of haplotype phase is increasingly important as we enter the era of large-scale sequencing because many of its applications, such as imputing low frequency variants and characterizing the relationship between genetic variation and disease susceptibility, are particularly relevant to sequence data. Haplotype phase can be generated through laboratory-based experimental methods, or it can be estimated with computational approaches. We assess the haplotype phasing methods that are available, with particular focus on statistical methods, and discuss practical aspects of their application. We also describe recent developments that may transform this field, particularly the use of identity-by-descent for computational phasing.

With recent technological advances, enormous amounts of genotype data are being generated, both from increasingly comprehensive and inexpensive genome-wide SNP microarrays and from ever more affordable whole-genome and whole-exome sequencing tools. However, the vast amount of information in these data is best exploited through phased haplotypes, which identify the alleles that are co-located on the same chromosome. Because sequence and SNP array data generally take the form of unphased genotypes, one does not directly observe which of the two parental chromosomes, or haplotypes, a particular allele falls on. Fortunately, new advances in both computational and laboratory methods promise improved determination of haplotype phase.

Methods for haplotype phasing have developed in response to improvements in technology that have changed the scale of genetic data. At first, genetic studies typically would assay only a single variant, and hence haplotype phase was irrelevant. As candidate gene sequencing became more accessible in the late 1980s, methods were developed for computational and experimental phasing of short regions containing a small number of genotyped polymorphisms. With the advent of genome-wide SNP microarrays and genome-wide association studies around 2005, new computational methods were developed to handle whole-chromosome data efficiently. Laboratory-based methods for experimental phasing of whole genome sequence data have also recently been developed.

The importance of haplotype phase information is increasing as we move into the era of large-scale sequencing. Applications of haplotype phase include understanding the interplay of genetic variation and disease,1 imputing untyped genetic variation,2–4 calling genotypes in microarray and sequence data,5–10 detecting genotype error,11 inferring human demographic history,12 inferring points of recombination,13 detecting recurrent mutation13 and signatures of selection,14 and modeling cis-regulation of gene expression.15

In this review we cover the historical and recent developments in methods for computational phasing of genotypes from population data sets and family data sets, and experimental methods for phasing single individuals. This review focuses mostly on computational methods, both because the authors’ expertise is in this arena, and because experimental methods are not yet cost-effective for large-scale use. We examine the strengths and weaknesses of the best existing methods, and consider a few examples of their use. Finally, we discuss recent developments and current challenges in phasing methodology.

Computational haplotype phasing

Computational methods pool information across individuals in order to estimate haplotype phase from genotype data. Unrelated individuals can be phased by considering sets of common haplotypes that can explain the observed genotype data. The number of unrelated individuals present in a sample is a critical factor in determining how well phase can be estimated; the more individuals, the better the estimation. Related individuals, by contrast, can be phased by considering haplotypes that are shared identical by descent between individuals within families. This within-family information on identity by descent (IBD) is much more informative for phase estimation than the haplotype frequency information used to phase unrelated individuals; however, haplotype frequency information across families or from the population can also be used to fill in the gaps in haplotype phase that are not determined by IBD sharing within families. Also, with unrelated individuals, some cryptic relatedness will exist that can be exploited with an IBD sharing approach. Thus, computational phasing of related and unrelated individuals are not completely separate problems.

Computational cost is an important factor when considering which computational phasing method to use. Generally, there is choice of algorithms and algorithm parameters and the researcher must select a trade-off between haplotype phase accuracy and computational cost. For large data sets of unrelated individuals, one wants a method that scales well with both number of markers and number of individuals. For family data, one wants a method that can handle the maximum family size present in the data (many methods scale exponentially with family size) and that also scales well with number of markers.

Computational phasing in unrelated individuals

Statistical approaches to phasing unrelated individuals rely on the modeling of haplotype frequencies. Where several haplotype configurations are possible for an individual’s genotypes, one can estimate, through statistical modeling of the data, the probability of any given haplotype configuration (Figure 1), and either pick the most likely configuration or output a set of configurations sampled from the posterior distribution. Other computational approaches, such as parsimony16,17 and long-range phasing13 (discussed below), are rule-based methods; they don’t model haplotype frequencies directly, but are based on the assumption that the haplotype configurations that are most likely are those that are seen in other individuals.

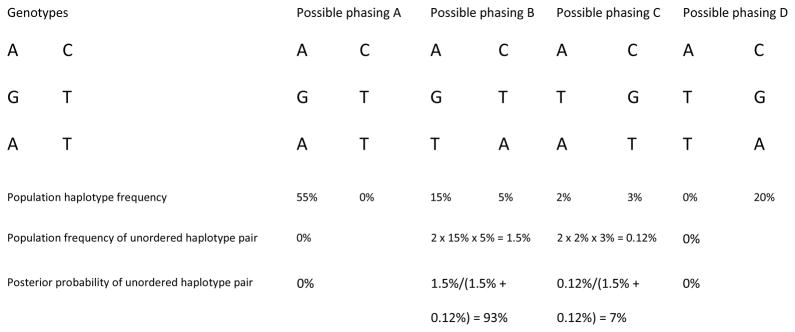
Figure 1. Statistical phasing of unrelated individuals using haplotype frequencies.

Figure 1

Consider one individual with heterozygous genotype at each of three SNPs in a region. There are four possible haplotype configurations consistent with the genotype data (A–D). Suppose haplotype frequencies are available from other individuals in the population at these sites (provided below each phasing pattern). These frequencies may have been estimated from population data without additional modeling (with the a priori assumption that all haplotype frequency configurations are equally likely) or with a model that accounts for the biological processes of recombination and mutation (such as the Li and Stephens model30).

The population frequency of a haplotype pair is obtained using the Hardy-Weinberg principle (independence of the two haplotypes within an individual); the factor of two in the frequency of the haplotype pairs accounts for both possible assignments of maternal and paternal origin to the two haplotypes. The posterior probabilities of the phased data are obtained from the population frequencies of the possible haplotype pairs. In this example, the posterior probability of phasing B (93%) is much greater than that of phasing C (7%).

Our description focuses on those methods that are most widely used or historically important. We present the methods in approximate chronological order. There are many other computational phasing methods in use which are described elsewhere.18

Clark’s algorithm

Clark’s algorithm19 was the first published method for haplotype phase inference for three or more markers in unrelated individuals. The method is based on utilizing unambiguous haplotypes (from individuals with at most one heterozygous marker) and parsimony (finding solutions that utilize the least number of unique haplotypes). The algorithm is suitable only for very tightly linked polymorphisms. When polymorphisms are not tightly linked there may be several reasonable haplotype phase assignments corresponding to an individual’s genotype, and the method does not provide a means of choosing between such assignments. Clark anticipated the next significant advance in phasing methodology by observing that the EM (Expectation-Maximization) algorithm could be used to phase small numbers of polymorphisms that are not tightly linked.19

EM algorithm

Early application of the EM20 algorithm to the haplotype phasing problem21–23 involved treating all possible haplotype configurations as a priori equally likely. This phasing method is typically referred to as “the EM algorithm”, even though many other statistical phasing methods also use an EM approach as part of their algorithms. The basic EM algorithm works well for a small number of genetic polymorphisms (up to around 10), but quickly encounters computational constraints as the number of markers increases. The partition-ligation extension of the EM algorithm24 increases the number of polymorphisms that can be handled computationally. However, for larger numbers of markers the EM method is computationally expensive and loses accuracy by using a suboptimal model for haplotype frequencies. More accurate phasing can be obtained by better a priori modeling of probabilities of haplotype configurations, as is done by the coalescent-based and hidden Markov model methods described below.25 Many software implementations of the EM algorithm exist, including Arlequin26 and PL-EM.24

The EM algorithm is useful when a small number of polymorphisms in a short gene or haplotype block are to be studied. Clark’s algorithm can also be used for this purpose, and PHASE (see below) is also suitable and would in most cases be a better choice. One application in this setting is haplotypic association testing. For example, Drysdale et al.27 used Clark’s algorithm to phase 13 tightly linked SNPs in the beta-2 adrenergic receptor gene and found that a haplotype pair was significantly associated with bronchodilator response to β agonist in asthmatics, whereas individual SNPs were not. A second application is determining whether a polymorphism seen in multiple populations has a single origin or has independently arisen multiple times. This question can be answered by investigating whether the polymorphism occurs on a single haplotype background (single origin) or multiple haplotypes (multiple origins). For example, by using the EM algorithm on 5 SNPs, Rosenberg et al.28 determined that the methylenetetrahydrofolate reductase 677T polymorphism is associated with a common haplotype in individuals from European, Asian and African populations. This finding indicates that the polymorphism may have occurred on a haplotype that had a selective advantage.

Coalescent-based methods and hidden Markov models

Approximate coalescent models29 were a breakthrough for modeling population haplotype frequencies.30–32 These models recognize that new haplotypes are derived from old haplotypes by the processes of mutation and recombination. Because mutation and recombination events are rare over small genomic distances, haplotypes tend to look similar to each other. Thus, for example, if one sees the haplotypes 1100 (where 0 and 1 represent two possible alleles at each of 4 polymorphic sites) and 0001 in the sample, one may also be somewhat likely to see the haplotype 1101 (formed by recombination) or 0011 (formed by mutation), but one is less likely to see the haplotype 1111 (formed by a recombination and a mutation). This approach forms the basis of many population-based statistical phasing methods, including PHASE,25,33 fastPHASE,34 MACH4 and IMPUTE2.35 In each case, the approximate coalescent gives rise to a hidden Markov model (HMM), and its parameters are estimated with the use of iterative algorithms such as the stochastic EM algorithm.36,37 The methods are described briefly below; additional details and comparisons of the methods are given in Box 1.

Box 1. Approximate coalescent and HMM methods for computational phasing of unrelated individuals.

An HMM has underlying hidden states that are not directly observed. In haplotype phase inference, these states represent in some way the underlying true haplotypes. Transition probabilities determine the ways in which the hidden states can change from one chromosomal position to another, and emission probabilities links unobserved states to the observed data.

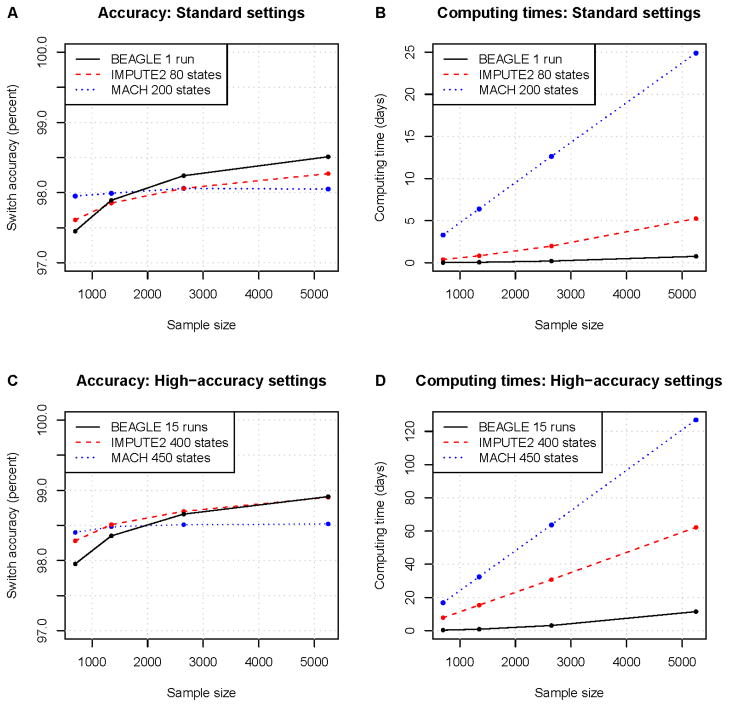
In the Li and Stephens30 framework used by MACH4 and IMPUTE2,35 the hidden states are “template haplotypes”. These template haplotypes are haplotypes already estimated within the sample. During each iteration of the estimation procedure, each individual’s haplotypes are estimated by using template haplotypes previously estimated in other individuals. Over successive iterations the haplotype estimates improve, converging towards an optimal solution. MACH uses a random subset of sample haplotypes as templates, whereas IMPUTE2 uses a subset of haplotypes that are selected to be similar to the haplotypes of the individual currently being estimated. IMPUTE2’s strategy appears to permit more improvement in accuracy as sample size increases when model complexity (the number of states) is held constant (see Figure 2). As part of the estimation procedure, MACH also estimates the transition probabilities for the hidden states (essentially the recombination rates) and the emission probabilities (representing the mutation rates). In contrast, IMPUTE2 takes as input the effective population size and recombination rates and uses these to derive transition rates and emission probabilities. This difference may account for some of the difference in computing times between the two methods (Figure 2).

The model used by PHASE (v2.1) is quite similar to the Li and Stephens framework, but adds an additional set of parameters: the coalescent times between a given haplotype and the underlying template haplotype. All haplotypes, other than those of the individual being re-estimated at each step, are used as hidden states (templates), unlike MACH and IMPUTE2 which use only a subset of haplotypes as templates. This is one factor underlying the difference in computation times. Another factor is that PHASE uses Markov chain Monte Carlo to explore the space of all possible solutions, whereas MACH, IMPUTE2, as well as BEAGLE and fastPHASE use stochastic EM to converge towards the most probable solutions.

BEAGLE40 forms an HMM by locally clustering the haplotypes at each marker position along a chromosome. The haplotypes are locally clustered in such a way that haplotypes in the same cluster tend to have similar probabilities for alleles at downstream markers. The haplotype clusters are the hidden states. At each iteration of the algorithm, new haplotype estimates are sampled from the current state of the HMM conditional on the genotype data, and these haplotype estimates are used to build a new HMM. The model is parsimonious in several ways. First, the clustering of haplotypes keeps the number of underlying hidden states relatively low. Second, the model only considers a small subset of all possible transitions between states at one position and states at the next position (whereas the Li and Stephens framework allows for all possible transitions). The transitions considered are those implied by the haplotype estimates used to build the current model. These differences between BEAGLE and the Li and Stephens framework are described in more detail elsewhere.46

The fastPHASE34 method also locally clusters haplotypes, however the way the clustering is performed is different to that of BEAGLE. BEAGLE’s approach allows different positions to have different numbers of clusters (hidden states), whereas fastPHASE uses the same number of clusters at each position. For small sample sizes the optimal number of clusters can be determined and used, but for large sample sizes the optimal number of clusters would be larger than is computationally feasible. FastPHASE is similar to PHASE, MACH and IMPUTE2 (but different from BEAGLE) in allowing for all possible transitions between states from one position to the next.

PHASE25,33 was for some time considered a gold standard for accuracy among population-based haplotyping algorithms.38 It is still useful for small genomic regions, but it is very slow compared to newer algorithms. PHASE is suitable for moderately small numbers of markers (up to 100) and small sample sizes (up to several hundred individuals). For large genomic regions other methods, such as those described below, should be used. Available software includes PHASE itself and a faster implementation, SHAPE-IT.39

FastPHASE34 was an important milestone because this algorithm made it possible to phase genome-wide SNP array data. For small numbers of individuals (up to one hundred) it is only a little less accurate than PHASE.34 The speed of FastPHASE is partly achieved by use of a parsimonious clustering of haplotypes. For small sample sizes, this clustering captures almost all of the information. However, for larger sample sizes computational feasibility is maintained at the cost of loss of information, leading to less accurate haplotypes than can be achieved with some of the more recent methods.40

BEAGLE40 is based on an HMM that does not explicitly model recombination and mutation, although these aspects are implicitly captured. The model clusters haplotypes at each locus, and the clustering adapts to the amount of information available so that the number of clusters increases globally with sample size and locally with increasing linkage disequilibrium (LD). Relative to fastPHASE, BEAGLE is an order of magnitude faster and is more accurate for medium and large sample sizes (>1000 individuals), but is less accurate for small sample sizes (100 individuals).40 BEAGLE is not well-suited for very small numbers of markers in a region (fewer than 100).

MACH4 and IMPUTE235 are new additions to the set of available statistical phasing methods. Both methods have been used primarily for the imputation of untyped variants but can also be used for haplotype phase inference, and are based on the same approximate coalescent model.30 These methods can handle larger data sets than PHASE while giving greater accuracy for large sample sizes than fastPHASE. In Figure 2 we compare the performance of BEAGLE with that of MACH and IMPUTE2, as the haplotype phasing performance of MACH and IMPUTE2 has not previously been examined in detail. Using parameters suggested in the documentation for each program (Fig. 2a–b), MACH has the highest accuracy for the smaller sample sizes, and BEAGLE had the highest accuracy for larger sample sizes. There was more than an order of magnitude difference in computing times between the method with the fastest computing time (BEAGLE) and the method with the slowest computing time (MACH). The accuracy of all programs can be improved at the cost of increased computing time (Fig 2c–d). For MACH and IMPUTE2, increasing the model complexity by increasing the number of HMM states allows the methods to make better use of the information in the data and thus obtain more accurate results, though the program will take longer to run. For BEAGLE, accuracy is improved by combining the results from multiple runs.

Figure 2. Comparison of recent statistical haplotype phasing methods.

Figure 2

We compared phasing accuracy and computation time for BEAGLE 3.3.1,40 IMPUTE 2.1.235 and MACH 1.0.16.4 The sample was comprised of up to 5200 controls from the Wellcome Trust Case Control Consortium 284,85 and 44 offspring from the HapMap344 CEU trios (Utah residents with Northern and Western European ancestry) genotyped on Illumina Human1M SNP arrays. We evaluated accuracy for markers on chromosome 20 (21,166 markers after quality control filters). Phasing accuracy was measured in the HapMap trio offspring using the markers that have phase determined by parental genotypes. Accuracy is represented by switch error rate (see Box 1). BEAGLE was run with default settings with the low-memory option (use of the low-memory option does not affect accuracy but reduces memory usage at the cost of a 30–60% increase in computing time). To obtain results in a reasonable amount of time for MACH and to follow recommended practice for IMPUTE2, the data for MACH and IMPUTE2 were split into eleven 5.1 MB chunks and one 6.3 MB chunk, with 500 KB overlap for adjacent chunks. The two haplotypes for each individual were aligned across chunks using the phase of heterozygous genotypes near the center of the overlap region and the chunks were merged to yield a chromosome-wide phasing. Computing times are for the whole chromosome, and are obtained for MACH and IMPUTE2 by adding computing times for each chunk. A) and B) This comparison used parameter settings that are based on the current documentation for each program. Parameter settings for IMPUTE2 followed parameters in a prototype phasing script downloaded from the IMPUTE2 website: “–phase– include_buffer_in_output –stage_one -k 80 –iter 30 –burnin 10 –Ne 11500”. MACH options were “--round 50 --states 200 --phase”, as suggested in the MACH documentation. C and D) As above, but with increased model complexity or run-time for each method to obtain improved accuracy. BEAGLE was run 15 times and the results were combined by phasing successive heterozygotes using a majority vote from the 15 runs. MACH was run with 450 states (compared to 200 for the standard settings) and IMPUTE was run with 400 states (compared to 80 states for the standard settings).

One application of haplotype phase on a genome-wide scale is investigation of population structure. Auton et al.41 used BEAGLE to phase almost 4,000 individuals from four continental regions at over 400,000 SNPs genome-wide. They used the phased haplotypes to compare patterns of haplotype diversity between populations. For example, they found that Japan has lower diversity than Taiwan, and that South Eastern Europe has lower diversity than South Western Europe. Haplotype patterns can also be used to detect signatures of selection. Sabeti et al.42 used HapMap data43 that had been phased with PHASE to look for unusually long haplotypes, which are a signature of positive selection. They found hundreds of strong candidates across the genome. Another important application of genome-wide phasing is to pre-phase data before performing imputation. Although pre-phasing data prior to imputation is not necessary for some imputation programs, it can substantially speed up the imputation process, but also incurs a small loss in accuracy. The main imputation programs (including BEAGLE, MACH and IMPUTE2) are also phasing programs, and are typically used for the pre-phasing step, if it is required. The largest public reference panels used for imputation (HapMap43,44 and 1000 genomes8) are available in phased versions. Haplotype association testing can also be performed on a genome-wide scale using phased haplotypes.45–47

Making use of identity by descent (IBD)

A recent development in computational phasing of haplotypes is the use of IBD information. Even in a sample of “unrelated” individuals, distant relationships give rise to segments of IBD, which can be used for phasing as described in more detail in the next section. The IBD that is useful in this context is IBD that is due to a relatively recent shared ancestor, such as within the past 20 generations, which leads to detectable long segments of IBD.48,49 A rule-based version of this approach was pioneered by Kong et al.13 in their long-range phasing algorithm that was applied to the Icelandic population. In this study, IBD tracts were identified by searching for long genomic segments (≥10 Mb) for which two individuals shared an allele at all markers in the segment. The IBD-based approach worked particularly well in that setting because Iceland is a small, relatively isolated population, and because a high proportion of the existing population (over 10%) has been genotyped. Because the genotyped Icelandic sample was large relative to the population, for most individuals at most loci it is possible to find multiple other individuals who share a haplotype identical by descent that can be used for phasing. Consequently, it was possible to phase approximately 90–95% of heterozygous markers in the Icelandic sample. Direct application of Kong et al.’s rule-based approach to large outbred populations is not currently practical. An extrapolation from the Icelandic population presented in the Kong et al. study suggests that the successful application of the long range phasing algorithm would require at least 1% of an outbred population to be genotyped. It is likely that the applicability of IBD-based phasing can be extended to additional populations by employing more sensitive methods for detecting IBD and combining IBD-based phasing with population haplotype-frequency models. Software is available for long-range phasing using IBD.50,51 These programs are suitable for phasing large pedigrees or samples from small populations in which all individuals are closely related.

The long-range haplotypes generated by Kong et al. have been used for several interesting applications. Kong et al.52 used genealogy and the inferred haplotypes to determine the parental origin of alleles and to test for association with disease. They found several parental-origin-specific associations. Holm et al.53 used the inferred haplotypes for accurate imputation of a putative rare causal variant in other individuals, to obtain a stronger association signal. Kong et al.13 also showed that the haplotypes can be used to study fine-scale recombination and to study the inheritance of recurrent mutations.

In related individuals for whom pedigrees are available, Mendelian constraints (or, more generally, IBD constraints) provide information to determine the haplotype phase at many sites. For example, a parent–offspring pair must share one allele identical by descent at every position, and the identical by descent alleles at different sites on the same chromosome will be on a single haplotype in the child and on a single haplotype in the parent, provided recombination has not occurred between the sites in the transmission of the chromosome to the child. Figure 3 gives an example of the use of IBD to determine haplotype phase. More generally, if two individuals have IBD across a region on a chromosome, they must share one allele identical by descent at every position in the region, and the identical by descent allele will usually be on a single shared haplotype in both individuals. If one or both individuals have a homozygous genotype at a site within the region of IBD, the allele in the homozygous genotype must be the shared allele, so that the identical by descent allele is known, and the site is phased relative to all other sites in the region for which the identical by descent allele is known. Thus, for diallelic markers such as SNPs, haplotype phase is only unknown at positions where both individuals are heterozygous or not identical by descent, or where one individual has a missing genotype.

Figure 3. Use of IBD to determine haplotype phase.

Figure 3

Determining phase using IBD alone.

When two individuals are known to be identical by descent (for example, if they are a parent–offspring pair), the individuals share an allele at each marker and this allele is determined by the genotype data when one or both individual is homozygous. In this example, the two individuals, with unphased genotypes given in the left-most columns, are identical by descent. SNP 1 is heterozygous in both individuals and thus cannot be phased using the IBD but may be able to be phased using population haplotype frequencies (see below). SNP 2 is homozygous in individual 2, and so the shared haplotype must have the C allele. Analogously, SNPs 3 and 4 are homozygous in individual 1, so the shared alleles are T and G, respectively. SNP 5 is homozygous in both individuals so phasing is trivial. The inferred shared haplotype is shaded green. Use of IBD phasing alone gives phasing shown in the IBD-phased haplotype columns, in which the phasing of SNP 1 is unknown.

Determining phase using IBD and haplotype frequencies.

Consider the same two identical by descent individuals as above. Phase is determined by IBD at SNPs 2–5, but is not determined at SNP 1 which is heterozygous in both individuals. Only haplotype phasings that satisfy the IBD-phasing constraints need be considered. Here the two identical by descent individuals are phased jointly, so the joint phase at SNP 1 must be consistent with the IBD, and the identical by descent haplotype is only included once in the probability of the haplotype configuration. The inferred identical by descent haplotype is shaded. Haplotype phasing A is much more probable (94%) than phasing B (6%).

Further information on haplotype phase is obtained when more than two relatives are considered simultaneously. For example, in parent–offspring trios (mother–father–child), at diallelic markers the only positions at which phase is not determined are those where all three individuals are heterozygous (a small proportion of sites) or sites where one or more of the individuals has a missing genotype. Larger families contain even more information on haplotype phase, although this is not trivial to extract. Linkage programs such as GENEHUNTER54 can extract this information, although they assume that sites are in linkage equilibrium (not in LD). When sites are in LD, linkage programs that assume linkage equilibrium may falsely infer IBD where it is not present; this is a problem for pedigrees with many ungenotyped individuals and leads to incorrect phasing.55 Moreover, because these methods assume that markers are in linkage equilibrium, they can not utilize information from population haplotype frequencies.

As an example of family-based phasing, Roach et al. analyzed sequence data on a nuclear family (two parents and two children). They inferred inheritance patterns and hence haplotype phase. They were able to use the phase information to look for genes in which the affected children had compound heterozygosity for dysfunctional variants56. This enabled them to determine the genes responsible for two rare syndromes affecting the children.

Long-range phasing in families

The Kong et al.13 approach to IBD detection and phasing in unrelated individuals can also be applied to data from related individuals, and this approach can be used with sites in LD. However, diallelic markers can only be phased when one of the related individuals is homozygous or when one of the related individuals can be phased from other IBD relationships, so that the allele on the shared haplotype can be determined. The use of IBD to phase related individuals provides essentially perfect phasing (barring genotype error and recent mutation) over long chromosomal regions at sites which can be phased with the IBD information alone (i.e. not at sites at which the identical by descent individuals are all heterozygous). Fortunately, population haplotype frequency information is also available to estimate the phase at those ambiguous sites. Haplotype frequency information can provide accurate phasing over very short genomic regions, and thus in principle can fill in the gaps to provide an overall phasing that is highly accurate (Figure 3). The use of haplotype frequency information with IBD-based phasing is currently an active area of research.

Utilizing population haplotype frequency information

Some methods use both IBD and population haplotype frequency information to phase related individuals, although the existing methods are limited in various ways. It is possible to use family information in conjunction with the EM algorithm to estimate haplotype phase.57,58 This approach can only analyze very small genomic regions. MERLIN is a linkage program that allows limited LD in the form of clusters of tightly-linked markers.59 This approach to LD modeling is not adequate for highly dense genotype data such as those generated from current genome-wide SNP microarrays or sequencing. BEAGLE3, SHAPE-IT39 and modifications of other programs38 use IBD and haplotype frequencies to phase parent–offspring trios. These methods work well for trios and parent–offspring pairs, but are not easily extended to larger families with multiple offspring or multiple generations due to intrinsic limitations in the algorithms.

Ignoring relationship

It is possible to phase related individuals as if they were unrelated, utilizing only population haplotype frequency information. Figure 4 demonstrates that the haplotype phase of closely related individuals will be estimated more accurately than that of unrelated individuals even when the relationship information is ignored or unknown, as had been suggested previously.60 This result is because the occurrence of the same extended identical by descent haplotype several times in the sample helps in its estimation. Drawbacks of this approach are that it is possible to have inconsistencies between the haplotype phases of closely related individuals (that is, the phasing may imply the unlikely occurrence of several closely spaced recombinations, or imputed missing genotypes may not be consistent with Mendelian rules), and the accuracy of the phase estimation will not be as high as it could be if the relationships were fully utilized. Nonetheless, this approach provides a simple solution that will provide acceptable accuracy for many applications.

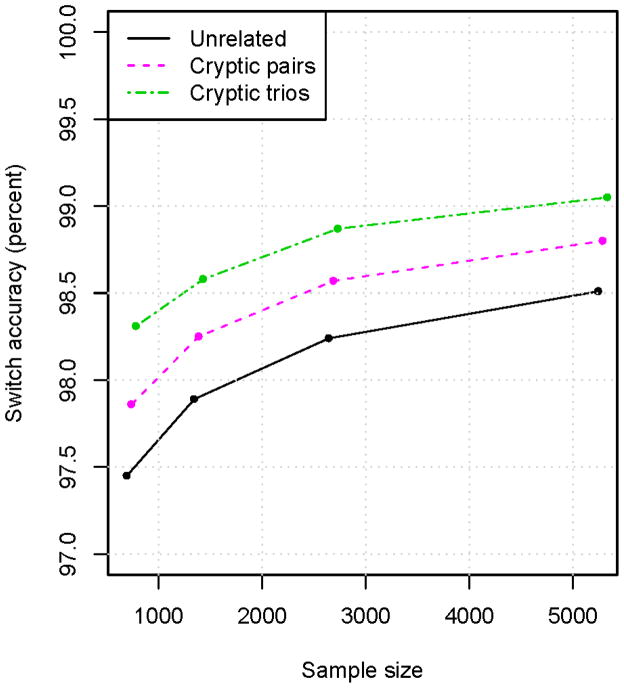
Figure 4. Accuracy of statistical phasing of cryptic relatives when relationship is not explicitly accounted for.

Figure 4

The same sets of individuals were phased as in Figure 2, with the addition of one parent of each HapMap CEU child (“Cryptic pairs” results) or both parents (“Cryptic trios” results). Phasing was performed with BEAGLE assuming all samples are unrelated. The “Unrelated” results are identical to those for BEAGLE in Figure 2A, and do not include any of the parents. It can be seen that adding relatives to the phase estimation greatly improves phase accuracy even when treating the individuals as unrelated. The phase accuracy would be significantly further improved by using the known relationships during the phase estimation.

Factors influencing computational phasing accuracy

A number of factors influence the achievable computational phasing accuracy. These include sample size, marker density, genotype accuracy, relatedness in the sample, ethnicity and allele frequency.

Sample size

Other factors being equal, the larger the sample size, the greater the haplotype phasing accuracy (see Figure 2), particularly when the statistical model can incorporate the large amount of information on population haplotype frequencies contained in larger data sets.40 This applies to family data as well as to unrelated data3 when haplotype frequency information is used to phase those sites that do not have phase determined by IBD. Thus a simple and powerful strategy for improving haplotype phase accuracy is increasing the sample size via use of a reference panel of individuals from the same population and using a phasing method that can make effective use of the additional data.

Marker density

Whether marker density results in improved or reduced accuracy depends on the measure of accuracy being considered (see Box 2). On a per-marker basis, haplotype estimates are more accurate with denser data. However, on a regional basis with an absolute measure of accuracy (totally correct haplotype over a region), having greater marker density results in more opportunity for error and thus lower accuracy.

Box 2. Metrics for comparing haplotype phasing methods.

Three primary metrics are used to measure computational haplotype phase accuracy: haplotype accuracy, imputation accuracy, and switch error. It is generally sufficient to use one rather than all of the metrics when comparing algorithms because the metrics tend to produce similar rankings. The haplotype accuracy and switch error metrics require the existence of gold standard phased data. This gold standard may come from nuclear family data or from experimental phasing. When gold standard data are available, switch accuracy is usually the most informative metric. The imputation accuracy metric is unique in that it can be applied to any data set without requiring the existence of “gold standard” phased data. Thus, one can use this metric to make sure that the haplotype inference procedure is performing properly, or to choose which program settings to use.

Haplotype accuracy

This measure relates to the proportion of haplotypes that are inferred correctly over the whole region of interest. This metric is typically relevant only for small numbers of markers, as the chance of correctly phasing a large region is very small, even for the best statistical phasing methods. This metric can be applied to simulated data for which the true haplotype phase is known, or to real data for which Mendelian constraints from closely-related individuals determine the true phase at most sites.

Imputation accuracy

Haplotype phasing algorithms generally impute sporadic missing data as part of the phasing algorithm. One can mask some of the genotypes (i.e. set some genotypes to ‘missing data’ status) and determine the proportion of imputed alleles that are correctly imputed by the phasing algorithm. This metric can be applied to any data set because it does not require knowledge of the true haplotype phase.

Switch error

When comparing an inferred haplotype phase to the true haplotype phase, one can count how many switches (recombination events in the inferred phased haplotypes) are required to obtain the true haplotype phase. One can express this comparison as a rate: the number of switches required divided by the number of opportunities for switch error, which is the number of heterozygote markers in the individual’s genotype minus 1 (the first heterozygote marker can be assigned arbitrary phase).

Metrics for experimental phasing accuracy

The experimental phasing of an individual’s genotypes is independent of a statistical phasing using a reference panel (see Computational phasing in unrelated individuals), provided that statistical phasing has not been used as part of the experimental phasing procedure. The statistical phase of pairs of heterozygous SNPs for which LD is high (e.g. D’>0.9 or =1), will be highly accurate, and can be compared with the experimental phase to obtain a rate of concordance.69,70 Similarly, if the individual has close relatives who have been genotyped, Mendelian or IBD constraints (see Computational phasing in related individuals) can be used to accurately determine the phase of many SNPs, and the proportion of SNPs at which the experimental phase is discordant can be calculated.73,74 In addition, for experimental phasing methods, the proportion of heterozygous SNPs at which phase can be determined is an important factor, as this is typically much less than 100%, and the proportion of SNPs at which the genotype is incorrect or missing also needs to be considered as this can be lower than for methods generating unphased data.

Genotype accuracy

Genotype accuracy influences haplotype phase accuracy since at least one of the two estimated haplotypes for an individual must be wrong whenever a genotype is mis-specified. When genotype data are noisy or incomplete, as is the case with low-coverage sequence data, one solution is to phase genotype likelihoods rather than called genotypes. Genotype likelihoods capture the uncertainty in the genotype data, and both EM-based and HMM based phasing algorithms can be adapted to phase genotype likelihood data.5,6 With genotype likelihood data, posterior genotype probabilities and haplotype phase are estimated simultaneously, which increases the accuracy of both tasks.6,8,61

Degree of relatedness

Known relatedness, if utilized along with haplotype frequency (such as in parent–offspring trios), results in markedly superior haplotype phase estimation compared to the use of only unrelated individuals.38 As we showed above, even if closely related individuals are treated as unrelated individuals, their haplotypes will be estimated more accurately than those of unrelated individuals.

Sample ethnicity

African populations have more haplotype diversity, and lower levels of LD, compared to non-African populations such as Europeans. Allele frequencies and density of polymorphisms are confounding factors when comparing accuracy across ethnicities and the comparison will depend on the accuracy metric and also, perhaps, on the phasing algorithm used. Overall, there does not seem to be a clear pattern of differences in phasing accuracy between populations from different continents.3,38,62 In the context of genotype imputation, including samples from closely related populations in the imputation reference panel can improve genotype imputation accuracy, particularly for low-frequency variants.63,64 This suggests that when the sample is small and no other individuals from the same population are available to use as a reference panel, one can improve haplotype estimation accuracy by including samples from other populations, particularly those from closely related populations such as other populations from the same continent. For samples with admixed ancestry, such as African Americans, including samples from the ancestral populations may improve phasing accuracy.62

Allele frequency

Rare variants are difficult to phase computationally, because to obtain high-confidence phase information a variant must be seen several times within its haplotype context. In particular, computational approaches cannot phase mutations that have arisen de novo in an individual, unless data on the individual’s offspring are available. For this important class of variants, experimental phasing methods are required.

Experimental phasing

Experimental phasing is expensive and labor-intensive. Nonetheless, when very accurate long-range haplotypes are required, and close relatives are not available for IBD-based computational phasing, experimental phasing methods are available that can be applied during the data generation. Also, sequencing technologies automatically produce some information on phase, and methods to use that information are beginning to be developed.

While several experimental phasing methods provide complete phasing of whole chromosomes, other methods provide phasing only for long or short haplotype fragments. In the latter case, computational methods must be applied to assemble overlapping fragments into larger haplotypes. This problem, known as the single individual haplotype reconstruction problem, is theoretically challenging and has received considerable attention.65 In most cases, population data are not utilized, but several recent methods utilize both experimentally derived haplotype fragments and population information.66,67

Whole genome experimental phasing

The human reference sequence generated by the International Human Genome Sequencing Consortium was produced by first creating large-insert clones, and then shotgun sequencing the clones68. The clone inserts are single haplotypes, resulting in haploid sequence. The same large-insert clone plus shotgun sequencing approach can be used to directly generate sequence on phased haplotypes, although it is extremely expensive on a whole-genome scale. Recently, Kitzman et al.69 combined this approach with next generation sequencing to produce whole-genome sequence data that was mostly phased (Box 3). The added cost of applying this approach, beyond the cost of the whole-genome sequencing, was approximately USD$4000 ($1000 labor and $3000 reagents) for the sequence of a single individual.69 Suk et al.70 used a very similar approach, and indicated a cost of under € 6000, including the cost of the whole-genome sequencing. These methods do not provide completely phased chromosomes, because the phased haplotype fragments must be pieced together, which can incur errors. Suk et al. used ReFHap71 to assemble the fragments, while Kitzman et al. used a reimplementation of HapCUT.72 Suk et al. were able to phase 99% of SNPs, and the phased blocks had N50 length of 1 Mb (50% of resolved sequence is in a block of length at least 1 Mb), whereas Kitzman et al had lower coverage with 94% of SNPs phased into blocks with N50 length of 400 kb. A disadvantage of these approaches is that although large chromosomal segments can be phased, the segments may not be accurately stitched together due to missing phase information across regions of homozygosity exceeding fosmid size (40kb).70

Box 3. Recent methods for whole-genome experimental phasing.

These methods separate whole chromosomes (sections a–c, below) or long haplotypes (section d) using a variety of approaches. The separated chromosomes are either tagged individually or first combined into pools in such a way that most pools will contain at most one copy of each homologous chromosome or haplotype. The chromosomes are then sequenced or genotyped. All these methods are at the proof-of-concept stage, so it is difficult to know which of these, if any, will develop into a widely used protocol.

  1. Ma et al.74 arrested cells in metaphase, then spread chromosomes and microdissected them into subsets. Some subsets may contain two homologous copies of a chromosome, which cannot then be phased using that subset. They then genotyped each subset with a whole-genome genotyping array. Phased genotypes are available for chromosomes that had a single homologous copy in one of the subsets.
  2. Yang et al.83 used fluorescence-activated cell sorting (FACS) to separate individual chromosomes; these were amplified and tagged before sequencing, to enable reads to be mapped back to specific chromosome copies.
  3. Fan et al.73 developed a specialized microfluidic device to capture a single metaphase cell, and then partition the 46 chromosomes. Each chromosome was typed to determine its identity. Two pools were constructed containing only one copy of each homologous chromosome. Each pool was genotyped separately with a whole genome genotyping array to obtain phased genotypes.
  4. Kitzman et al.69 created a fosmid library of long haplotypes. These were separated into 100 pools. The probability that a given pool contains two non-homologous copies of the same chromosomal region is low. Barcode-labeled shotgun libraries were constructed from each pool. These were sequenced at low depth (2–3x). The barcodes were used to assemble the shotgun reads back into the haplotypes contained in the fosmid libraries. In addition, the individual was sequenced using standard next generation sequencing, with higher depth (15x). The unphased genotypes were determined from this sequencing, and then the haplotypes from the earlier step were used to determine haplotype phase.

Other approaches to experimental phasing are based on various other means to separate homologous chromosomes or haplotype fragments before genotyping or sequencing. Some of these methods can phase whole chromosomes. A recent method that enables whole-genome phasing in an automatable approach is the use of a specialized microfluidics device to separate chromosomes from a single cell in metaphase.73 The separated chromosomes can then be sequenced or SNP-genotyped (Box 3).

One application of experimentally phased whole-genome sequence is population genetics analysis. Kitzman et al.69 analyzed experimentally phased sequence of a Gujarati Indian individual and determined that the novel variants mostly fall on haplotypes that are not European-like. Another application is clinical interpretation of personal genomes. Suk et al.70 found 171 genes with two or more potentially severe mutations (amino acid changes predicted to alter the expressed protein) in the genome of a German individual, of which 159 were experimentally phased. Of these, 86 were in cis (on the same haplotype) and 73 in trans (compound heterozygosity). Configurations in cis leave one protein unchanged, which is likely to be less damaging. A further potential application of experimental phasing is determination of HLA haplotypes70,73 for donor-recipient matches in transplant medicine. More work is needed to assess whether the level of accuracy is sufficiently high for this application.

Whichever method is used, whole genome experimental phasing is more expensive than generating unphased whole genome data. The methods require an initial processing step, such as developing fosmid libraries or separating chromosomes. As such methods become more mainstream, it is likely this initial processing will be automated, saving time and reducing costs. Nonetheless, additional equipment and/or reagents are needed for this step. Further, the sequencing or genotyping following the initial processing tends to involve some additional sequencing or genotyping beyond that required for generation of unphased data. For example, Kitzman et al.69 and Suk et al.70 generated unphased sequence data as well as the phased fosmid sequences to improve the quality of the final phased data, while Ma et al.74 estimate that five to six genome-wide genotyping arrays are needed per sample on average for their chromosome microdissection method (Box 3).

Phase information in sequence reads

Direct sequencing can also provide some information for phasing. Sanger sequencing produces reads that are relatively long (>700-base read lengths are possible75). The use of paired-end sequencing also provides information for haplotype phasing. When a read encompasses two or more heterozygous genotypes of an individual, the phase of the heterozygote genotypes is determined since each fragment from which a read or pair of reads is obtained is a single haplotype. Thus, if the fragments are long and sequence coverage is sufficiently high, a substantial amount of haplotype phase information can be obtained.76 Sanger sequencing is too expensive for whole-genome sequencing on a large scale, but recently developed real-time, single-molecule sequencing methods are much cheaper, and these methods can yield sequence reads that exceed 1 kb.77,78 Long read lengths may permit direct phasing from experimental sequence reads with sufficient sequence coverage.

Next-generation sequencing technology is considerably less expensive than Sanger sequencing, but the reads are shorter, providing less information for phasing.77 Nonetheless, short reads, especially when they are paired-end reads, provide some information for phasing that can be incorporated into computational phasing.66,67 Software for using phase information from next-generation sequence reads include the Haplotype Improver software67 and the “read-backed phasing” algorithm incorporated in the Genome Analysis Tool Kit software.79

While whole genome experimental phasing is likely to remain a niche application due to its cost and complexity, the use of phase information from sequence reads is likely to be increasingly important. At present, phase information from sequence reads is not sufficient to fully determine haplotype phase, thus we expect to see the marriage of experimental and computational phasing as read information is incorporated into computational phasing methods.

Computational versus experimental phasing

There are several factors to consider when choosing whether to perform experimental phasing, computational phasing with related individuals or computational phasing with unrelated individuals. In terms of cost and feasibility, computational phasing in unrelated individuals is the most simple and inexpensive approach. Computational phasing in related individuals is straightforward if related samples are available and if the relationships are simple (in particular, parent-offspring pairs or trios are easily handled). The use of parent-offspring trios increases genotyping or sequencing cost threefold if the additional two individuals in each trio are not otherwise of interest. Experimental phasing increases data generation cost by two- to five-fold, requires high levels of technical expertise and may require investment in specialized equipment. Of the existing whole-genome experimental methods, the fosmid-based approaches69,70 appear to be least expensive (approximately two-fold increase in cost over standard sequencing), although the resulting haplotype phase has some gaps in coverage. Most types of phasing, excluding only the methods based on whole chromosome separation, require more computing resources than typically found in a desktop PC, and at least a moderate level of bioinformatics expertise.

Computational phasing in unrelated individuals provides accurate phasing of common SNPs over small regions when the sample is large or a large reference panel is used. This is adequate for a number of applications such as haplotypic association testing, imputation of ungenotyped common SNPs, and comparing haplotypic diversity across populations. However the accuracy is not high enough for some other applications, such as investigating compound heterozygosity, in which the variants of interest are of low frequency.

Rare and low frequency SNPs may be phased by genotyping/sequencing of related individuals or by experimental phasing. Both approaches will provide highly accurate phase at most SNPs, whether rare or common, and will provide phase over long chromosomal regions or whole chromosomes. De novo mutations can be phased with experimental approaches or with data from offspring (if available). With most phasing methods, one can expect to have some positions at which phase is unknown or incorrectly estimated. For example, phase is not known with certainty at SNPs for which parent-offspring trios are all heterozygous (although the use of population data may allow these positions to be phased with a reasonably high level of confidence). As another example, fosmid-based experimental haplotyping results in long blocks of phased haplotype, with phase unknown across block boundaries. In addition to the gaps in phase, the phased haplotypes may also be incorrect at some positions due to underlying genotype or sequence errors.

Current challenges and future directions

The incoming flood of large-scale sequence data presents challenges for haplotype phasing. Computational phasing is difficult for low frequency variants, and experimental phasing is currently too expensive for use on a large scale. Developments in statistical and experimental methods promise to meet these challenges. It remains to be seen whether whole-genome experimental phasing will end up being sufficiently inexpensive and automatable for common use, but the recently proposed methods suggest some promise. The use of phase information from short reads together with statistical information from haplotype frequencies is another area of development. Next-generation sequence-read lengths are increasing in size as the technology develops, thus providing increased information about phase, although improved statistical methodology is needed to fully exploit this information.

To obtain improved computational phasing of data from unrelated individuals, there is a critical need for large panels consisting of thousands of individuals from different ethnicities. This will enable researchers with relatively small sample sizes to borrow information on haplotype frequencies, and to enable the use of IBD-based haplotype phasing for improved accuracy. There is also a need for large sets of individuals to use as reference panels for imputation. It would be advantageous if these panels were accurately phased, to save computation time in the imputation analyses. The 1000 Genomes Project8 is an important step toward these goals; however, larger sets of individuals from each major population would provide further benefits. For some continental groups that have been the focus of existing studies, such as Europeans, large panels can be obtained by combining existing resources, but there is a practical need for large reference panels that have had careful quality control filtering and that have been accurately phased to be available as a single unified data set.

Another area of future development is the expansion of phasing algorithms to consider multi-allelic markers and copy number variants.80 Virtually all of the existing methods for the statistical inference of haplotype phase assume diallelic markers, although there are some exceptions.40,80,81 There is a need to extend existing methods to incorporate multi-allelic markers and to evaluate the accuracy of phasing methods when they are applied to data containing copy number variants.

Computational haplotype phasing is a computationally intensive task, as are other tasks associated with high throughput data, such as mapping sequence reads. As sequencing technology becomes less expensive and more ubiquitous, the computational challenges will become even more prominent. There is a need for even faster computational methods for haplotype phasing that are also highly accurate and able to exploit fully the information present in large samples. The use of IBD information latent in samples of “unrelated” individuals shows promise for increasing haplotype phase accuracy in large samples. Recent work on improved resolution of IBD detection48 should permit the extension of IBD-phasing from founder populations with a high proportion of individuals genotyped13 to outbred populations with a lower proportion of genotyped individuals.

Finally, computational haplotype phasing of related individuals that makes use of both relationship (IBD constraints) and haplotype frequencies is a remaining challenge area. As the pendulum moves back from the common-disease common-variant hypothesis with its focus on association studies in unrelated individuals to a greater focus on rare variants that are most easily studied in family data,82 methods for analysis of related individuals will be increasingly important.

Acknowledgments

This study was supported by the National Institutes of Health awards R01HG005701 and R01HG004960. This study makes use of data generated by the Wellcome Trust Case-Control Consortium. A full list of the investigators who contributed to the generation of the data is available from wtccc.org.uk. Funding for the project was provided by the Wellcome Trust under award 076113 and 085475. The content of this study is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health or the Wellcome Trust.

Glossary

EM algorithm

An iterative approach for finding the values of the unobserved data (such as haplotype phase) that maximize the statistical likelihood of the observed incomplete data. Although the likelihood increases with each iteration, the approach is not guaranteed to find the global maximum

Posterior distribution

Probabilities that account for the prior information and the information in the data. For haplotype phase estimation, the posterior distribution accounts for all available information, including the genotypes and the estimated population haplotype frequencies

Hidden Markov models (HMMs)

A mathematically elegant and computationally tractable class of models in which the observed data are generated by an unobserved Markov process. A Markov process is a probabilistic process in which the distribution of future states (e.g. states further along the chromosome) depends only on the current state and not on previous states

Linkage disequilibrium (LD)

Non-independence (correlation) between genetic variants at the population level. In general, LD decreases with genomic distance and is not present between variants on different chromosomes

Identity by descent (IBD)

Two haplotypes are identical by descent if they are identical copies of a haplotype inherited from a common ancestor

Approximate coalescent

The coalescent is a model for the process by which the ancestry of alleles converges when looking back in time. An approximate coalescent is a model that generates patterns of genetic variation that are similar to patterns generated by the coalescent, but that is computationally simpler

Reference panel

A collection of samples which are not of direct interest but that are included in an analysis for the purposes of increasing statistical power or accuracy for the samples of interest. Reference panels are commonly used for genotype imputation and can also be used for haplotype phasing

Large-insert clones

Large haplotype fragments inserted into, for example, bacterial artificial chromosomes (BACs)

Shotgun sequencing

A sequencing method in which DNA is randomly sheared into small fragments before being sequenced

Paired-end sequencing

Sequencing of haplotype fragments from each end. The two sequenced ends are typically separated by a gap

Metaphase

A stage of mitosis at which chromosomes are highly condensed, facilitating their separation for some experimental phasing methods

Fluorescence-activated cell sorting (FACS)

A type of flow cytometry in which individual particles (such as chromosomes) are separated and fluorescence intensities (from earlier staining) are measured

Compound heterozygosity

The presence of two deleterious variants located in the same gene, but on different chromosome copies of an individual. One can distinguish between compound heterozygosity and the occurrence of two variants on the same chromosome copy by determining the haplotype phase

Genotype likelihood

A statistical likelihood that encapsulates the relative evidence for each possible genotype call

Imputation

In the context of this article, the estimation of missing genotype values by using the genotypes at nearby SNPs and the haplotype frequencies seen in other individuals

Genotype calling

Estimating genotype values from raw data. Genotyping technology provides information about the underlying genotype, typically in the form of signal intensities or read counts of the two alleles. Statistical techniques are used to resolve this information into genotype calls. Typically information across individuals is used, and correlation across SNPs (i.e. haplotype phase) is also helpful

Partition-ligation

A divide-and-conquer strategy designed to reduce the computational burden phasing methods that do not scale well with increasing region size. A large region is divided up into smaller regions, and haplotype phase estimates from the smaller regions are used to limit the possibilities when phasing the large region

Admixed ancestry

An individual has admixed ancestry if he or she has recent ancestors deriving from different continental populations

Microfluidics

The manipulation of fluids on a very small scale. This approach can be used to separate individual chromosomes before sequencing for experimental phasing

Haplotype block

A short genomic region within which inter-marker linkage disequilibrium is relatively strong

Fosmid

A type of hybrid DNA molecule comprising bacterial DNA and a section of genomic DNA of length approximately 40kb

Barcode-labelling

Tagging of each sample with a unique short sequence (barcode) before pooling samples. After sequencing, the sample corresponding to each read can be determined from the barcode

Cryptic relatedness

The undocumented existence of relatives within a sample

Footnotes

References