Линейное подпространство | это... Что такое Линейное подпространство? (original) (raw)

Линейное подпространство

Лине́йное простра́нство, или ве́кторное простра́нство — основной объект изучения линейной алгебры.

Содержание

1 Определение
2 Простейшие свойства
3 Связанные определения и свойства
4 Примеры
5 Дополнительные структуры
6 См. также
7 Литература
8 Ссылки

Определение

Линейное, или векторное пространство 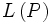$L \left( P \right)$ над полем P — это непустое множество L, на котором введены операции

сложения, то есть каждой паре элементов множества 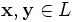$\mathbf{x}, \mathbf{y} \in L$ ставится в соответствие элемент того же множества, обозначаемый 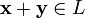$\mathbf{x} + \mathbf{y} \in L$ и
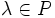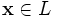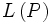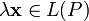умножения на скаляр (то есть элемент поля P), то есть любому элементу $\lambda \in P$ и любому элементу $\mathbf{x} \in L$ ставится в соответствии элемент из $L \left( P \right)$ , обозначаемый $\lambda\mathbf{x}\in L(P)$ .

При этом удовлетворяются следующие условия:

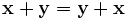$\mathbf{x} + \mathbf{y} = \mathbf{y} + \mathbf{x}$ , для любых 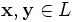$\mathbf{x}, \mathbf{y}\in L$ (коммутативность сложения);
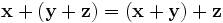$\mathbf{x} + (\mathbf{y} + \mathbf{z}) = (\mathbf{x} + \mathbf{y}) + \mathbf{z}$ , для любых 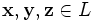$\mathbf{x}, \mathbf{y}, \mathbf{z} \in L$ (ассоциативность сложения);
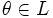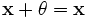существует такой элемент $\theta \in L$ , что $\mathbf{x} + \theta = \mathbf{x}$ для любого 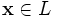$\mathbf{x} \in L$ (существование нейтрального элемента относительно сложения), в частности L не пусто;
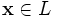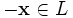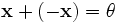для любого $\mathbf{x} \in L$ существует такой элемент $-\mathbf{x} \in L$ , что $\mathbf{x} + (-\mathbf{x}) = \theta$ (существование противоположного элемента).
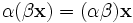$\alpha(\beta\mathbf{x}) = (\alpha\beta)\mathbf{x}$ (ассоциативность умножения на скаляр);
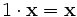$1\cdot\mathbf{x} = \mathbf{x}$ (существование нейтрального элемента относительно умножения).
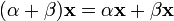$(\alpha + \beta)\mathbf{x} = \alpha \mathbf{x} + \beta \mathbf{x}$ (дистрибутивность умножения на скаляр относительно сложения);
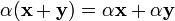$\alpha(\mathbf{x} + \mathbf{y}) = \alpha \mathbf{x} + \alpha \mathbf{y}$ (дистрибутивность сложения относительно умножения на скаляр).

Элементы множества L называют векторами, а элементы поля P — скалярами.

Простейшие свойства

Нейтральный элемент 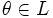$\theta \in L$ является единственным.
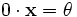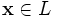$0\cdot\mathbf{x} = \theta$ для любого $\mathbf{x} \in L$ .
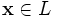Для любого $\mathbf{x} \in L$ противоположный элемент 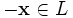$-\mathbf{x} \in L$ является единственным.
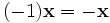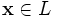$(-1)\mathbf{x} = -\mathbf{x}$ для любого $\mathbf{x} \in L$ .
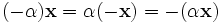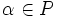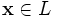$(-\alpha)\mathbf{x} = \alpha(-\mathbf{x}) = -(\alpha\mathbf{x})$ для любых $\alpha \in P$ и $\mathbf{x} \in L$ .

Связанные определения и свойства

Линейное подпространство или векторное подпространство ― непустое подмножество P линейного пространства L такое, что P само является линейным пространством по отношению к определенным в L действиям сложения и умножения на скаляр.
Конечная сумма вида

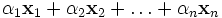
$\alpha_1\mathbf{x}_1 + \alpha_2\mathbf{x}_2 + \ldots + \alpha_n\mathbf{x}_n$

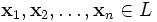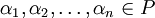называется линейной комбинацией элементов $\mathbf{x}_1, \mathbf{x}_2, \ldots, \mathbf{x}_n \in L$ с коэффициентами $\alpha_1, \alpha_2, \ldots, \alpha_n \in P$ .

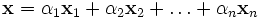$\mathbf{x} = \alpha_1\mathbf{x}_1 + \alpha_2\mathbf{x}_2 + \ldots + \alpha_n\mathbf{x}_n$ .

Примеры

Нулевое пространство, единственным элементом которого является ноль.
Пространство всех функций 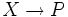$X\to P$ образует векторное пространство размерности равной мощности X.
поле вещественных чисел может быть рассмотрено как континуально-мерное векторное пространство над полем рациональных чисел.

Дополнительные структуры

См. также

Литература

Гельфанд И.М. Лекции по линейной алгебре. изд. МЦНМО, 1998.

Ссылки

Векторное пространство

Wikimedia Foundation.2010.

Полезное

Смотреть что такое "Линейное подпространство" в других словарях:

ЛИНЕЙНОЕ ПОДПРОСТРАНСТВО — векторное подпространств о, непустое подмножество L(линейного) векторного пространства Е над полем Ктакое, что L само является векторным пространством по отношению к определенным в Едействиям сложения и умножения на скаляр. Множество L+x0, где… … Математическая энциклопедия
Линейное пространство — Линейное пространство, или векторное пространство основной объект изучения линейной алгебры. Содержание 1 Определение 2 Простейшие свойства 3 Связанные определения и свойства … Википедия
ЛИНЕЙНОЕ УРАВНЕНИЕ — уравнение вида где А линейный оператор, действующий из векторного пространства Xв векторное пространство В, х неизвестный элемент из X, b заданный элемент из В(свободный член). Если 6=0, то Л. у. наз. однородным. Решением Л. у. наз. элемент… … Математическая энциклопедия
Линейное уравнение — уравнение, в которое неизвестные входят в 1 й степени (т. е. линейно) и отсутствуют члены, содержащие произведения неизвестных. Несколько Л. у. относительно одних и тех же неизвестных образуют систему Л. у. Решением системы Л. у. называют … Большая советская энциклопедия
Линейное отображение — У этого термина существуют и другие значения, см. Отображение (значения). Линейное отображение, линейный оператор обобщение линейной числовой функции (точнее, функции ) на случай более общего множества аргументов и значений. Линейные… … Википедия
ЛИНЕЙНОЕ УРАВНЕНИЕ — алгебраическое алгебраическое уравнение 1 й степени по совокупности неизвестных, т. е. уравнение вида Всякая система Л. у. может быть записана в виде где ти n натуральные числа; а ij (i=1, 2, . . ., т, j=1, 2, . . ., n) наз. коэффициентами при… … Математическая энциклопедия
Линейное нормированное пространство — В евклидовом пространстве понятие «длина вектора» понимается интуитивно как расстояние между его началом и концом. Наиболее важными свойствами «длины вектора» являются следующие: Длина нуль вектора, , равна нулю; длина любого другого вектора… … Википедия
Линейное преобразование — Линейным отображением (линейным оператором) векторного пространства LK над полем K в векторное пространство MK (над тем же полем K) называется отображение , удовлетворяющее условию линейности f(αx + βy) = αf(x) + βf(y). для всех и … Википедия
ЛИНЕЙНОЕ ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ В БАНАХОВОМ ПРОСТРАНСТВЕ — уравнение вида где A0(t), A1(t).при каждом t линейные операторы в банаховом пространстве Е, g(t) заданная, a u(t) искомая функции со значениями в Е;производная ипонимается как предел по норме Еразностного отношения. 1. Линейное дифференциальное… … Математическая энциклопедия
ЛИНЕЙНОЕ ПРЕОБРАЗОВАНИЕ — отображение векторного пространства в себя, при к ром образом суммы двух векторов является сумма их образов, а образом произведения вектора на число произведение образа вектора на это число. Если V векторное пространство, f заданное в нем Л. п. и … Математическая энциклопедия