Метод конечных разностей во временной области | это... Что такое Метод конечных разностей во временной области? (original) (raw)

Метод конечных разностей во временно́й области (англ. Finite Difference Time Domain, FDTD) — один из наиболее популярных методов численной электродинамики, основанный на дискретизации уравнений Максвелла, записанных в дифференциальной форме.

Содержание

Описание

FDTD относится к общему классу сеточных методов решения дифференциальных уравнений. Базовый алгоритм метода был впервые предложен Кейном Йи (Калифорнийский университет) в 1966 г. в статье «Numerical solution of initial boundary value problems involving maxwell’s equations in isotropic media» журнала «IEEE Transactions: Antennas and Propagation»[1]. Однако, название «Finite-difference time-domain» и аббревиатура FDTD были даны методу Алленом Тафловом (Северо-западный университет, штат Иллинойс).

В первоначальном узком смысле под FDTD подразумевалось использование базового алгоритма Йи для численного решения уравнений Максвелла. В современном более широком смысле FDTD включает в себя множество самых разнообразных возможностей: моделирование сред с дисперсными и нелинейными свойствами, применение различных типов сеток (помимо первично предложенной прямоугольной сетки Йи), использование методов постпроцессорной обработки результатов и т. д.

Примерно с 1990 г. метод конечных разностей стал основным для моделирования самых разных оптических приложений. Он может быть с успехом применен для решения широкого спектра задач: от моделирования сверхдлинных электромагнитных волн в геофизике (включая процессы в ионосфере) и микроволн (например для изучения сигнатурной радиолокации, расчёта характеристик антенн, разработки беспроводных устройств связи, в том числе цифровых) до решения задач в оптическом диапазоне (фотонные кристаллы, наноплазмоника, солитоны и биофотоника). К 2006 г. число публикаций, посвященных FDTD, достигло двух тысяч.

В настоящее время существует порядка 30 коммерческих программ FDTD, а также проекты с открытым исходным кодом (в числе которых несколько русских).

Алгоритм Йи

В уравнениях Максвелла изменение электрического поля E (частная производная) зависит от распределения в пространстве магнитного поля H (ротор). Аналогично, изменение поля H зависит от распределения в пространстве поля Е.

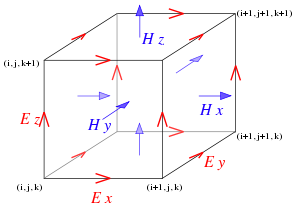
На этом наблюдении основан алгоритм Йи. Сетки для полей E и H смещены по отношению друг к другу на половину шага дискретизации времени и по каждой из пространственных переменных. Конечно-разностные уравнения позволяют определить поля E и H на данном временном шаге на основании известных значений полей на предыдущем.

При заданных начальных условиях алгоритм Йи дает эволюционное решение во времени от начала отсчета с заданным временным шагом.

Поля в ячейке сетки FDTD. Из таких ячеек составляется пространственная трёхмерная сетка Йи

Аналогичная (разделённая) сетка используется при решении задач гидродинамики (для давления и поля скорости).

Как и в любом другом разностном методе, в FDTD существует проблема неточного отображения границы тела на вычислительную сетку. Любая кривая поверхность, разделяющая соседние среды и геометрически не согласованная с сеткой, будет искажаться эффектом «лестничного приближения». Для решения данной проблемы можно использовать дополнительную сетку с большим разрешением в тех областях пространства, где расположены тела со сложной геометрической структурой[2]. Также можно видоизменять разностные уравнения в узлах сетки, находящихся вблизи границы между соседними телами[3]. Менее затратным методом является введение эффективной диэлектрической проницаемости вблизи границы между телами (subpixel smoothing) [4][5].

Численная схема FDTD не предполагает возможности табличного задания зависимости диэлектрической проницаемости от частоты. Однако, ее можно представить в виде апроксимации (фитинга) членами Дебая, Друде, Лоренца или Лоренца с поглощением. Такая аппроксимация не обязательно имеет физический смысл, и может быть получена численно, например с помощью программы [6].

Поглощающие граничные условия

Для того, чтобы ограничить объем сетки, в FDTD нужны особые поглощающие граничные условия, которые моделируют уход электромагнитной волны на бесконечность. Для этого использоваются поглощающие граничные условия Мура или Ляо[7], или идеально согласованных слои (Perfect Matched Layers, PML). Условия Мура или Ляо намного проще, чем PML. Тем не менее, PML — строго говоря, являющихся поглощающей приграничной областью, а не граничным условием как таковым — позволяет получить на порядки меньшие по величине коэффициенты отражения от границы.

Понятие идеально согласованных слоев (PML) было введено Жаном Пьером Беренже в статье журнала «The Journal of Computational Physics» в 1994 г.[8] Идея PML Беренже основывалась на разбиении исходных полей E и H на две компоненты, для каждой из которых должны решаться свои уравнения. Впоследствии были предложены усовершенствованные формулировки PML эквивалентные первоначальной формулировке Беренгера. Так, в одноосном PML (Uniaxial PML) используется анизотропный поглощающий материал, что позволяет не вводить дополнительные переменные и остаться в рамках исходных уравнений Максвелла[9]. Однако одноосный PML, как и PML в формулировке Беренже, не удобны тем, что в них отсутствует поглощение затухающих волн, что не позволяет помещать PML близко к рассеивающим телам. Этого недостатка лишен оборотный PML (Convolutional PML), основанный на аналитическом продолжении уравнений Максвелла в комплексную плоскость таким образом, что их решение экспоненциально затухает[10]. CPML также удобнее в ограничении бесконечных проводящих и дисперсных сред. Помимо этого математическая формулировка CPML обладает большей наглядностью и доступностью для понимания.

В некоторых случаях использование PML приводит к расходимости расчета FDTD. Эту проблему можно устранить путем помещения за PML дополнительной поглощающей стенки[11].

Численный эксперимент FDTD

Ход численного эксперимента FDTD выглядит следующим образом:

Достоинства и недостатки FDTD

Как и любой другой численный метод, FDTD свои достоинства и недостатки.

Достоинства:

Недостатки:

См. также

Источники

  1. ↑ Kane Yee (1966). «Numerical solution of initial boundary value problems involving Maxwell's equations in isotropic media». IEEE Transactions on Antennas and Propagation 14 (3): 302–307.
  2. ↑ S. S. Zivanovic, K. S. Yee, and K. K. Mei (1991). «A subgridding method for the Time Domain Finite-Difference Method to solve Maxwell's equations». IEEE Trans. Microware Theory Tech. 38: 471.
  3. ↑ T. G. Jurgens, A. Taflove, K. Umashankar, and T. G. Moore (1992). «Finite-difference time-domain modeling of curved surfaces». IEEE Trans. Antennas Propag. 40: 357.
  4. ↑ J. Nadobny, D. Sullivan, W. Wlodarczyk, P. Deuflhard, and P. Wust (2003). «A 3-D tensor FDTD-formulation for treatment of sloped interfaces in electrically inhomogeneous media». IEEE Trans. Antennas Propag. 51: 1760.
  5. ↑ A. Deinega and I. Valuev (2007). «Subpixel smoothing for conductive and dispersive media in the FDTD method». Opt. Lett. 32: 3429.
  6. ↑ Фитинг диэлектрической проницаемости. Архивировано из первоисточника 9 июня 2012.
  7. ↑ G. Mur (1981). «Absorbing boundary conditions for the finite-difference approximation of the time-domain electromagnetic field equations». IEEE Transactions on Electromagnetic Compatibility 23 (4): 377–382.
  8. ↑ J. Berenger (1994). «A perfectly matched layer for the absorption of electromagnetic waves». Journal of Computational Physics 114 (2): 185–200.
  9. ↑ S. D. Gedney (1996). «An anisotropic perfectly matched layer absorbing media for the truncation of FDTD lattices». IEEE Transactions on Antennas and Propagation 44 (12): 1630–1639.
  10. ↑ J. A. Roden and S. D. Gedney (2000). «Convolution PML (CPML): An efficient FDTD implementation of the CFS-PML for arbitrary media». Microwave and Optical Technology Letters 27 (5): 334–339.
  11. ↑ A. Deinega and I. Valuev (2011). «Long-time behavior of PML absorbing boundaries for layered periodic structures». Comp. Phys. Comm. 182: 149.
  12. ↑ I. Valuev, A. Deinega, and S. Belousov (2008). «Iterative technique for analysis of periodic structures at oblique incidence in the finite-difference time-domain method». Opt. Lett. 33: 1491.
  13. ↑ A. Aminian and Y. Rahmat-Samii (2006). «Spectral FDTD: a novel technique for the analysis of oblique incident plane wave on periodic structures». IEEE Trans. Antennas and Propagation 54: 1818.
  14. ↑ J. A. Roden, S. D. Gedney, M. P. Kesler, J. G. Maloney, and P. H. Harms (1998). «Time-domain analysis of periodic structures at oblique incidence: orthogonal and nonorthogonal FDTD implementations». Microwave Theory and Techniques 46: 420.
  15. ↑ K. R. Umashankar and A. Taflove (1982). «A novel method to analyze electromagnetic scattering of complex objects». IEEE Transactions on Electromagnetic Compatibility 24 (4): 397–405.

Ссылки

На русском

На английском

Литература

Методу FDTD посвящено множество публикаций, однако основная их масса на английском языке. Ниже приведены ссылки на некоторые из них:

Пионерские работы

Граничные условия

Проблемы геометрии (лестничная аппроксимация, разномасштабное моделирование)

Сложные материалы (дисперсия, поглощение, нелинейность и т.д.)

Прикладные расчёты

Модификации метода (гибридные, безусловно устойчивые и т.д.)