Отрицательные числа | это... Что такое Отрицательные числа? (original) (raw)

Отрицательное число — элемент множества отрицательных чисел, которое (вместе с нулём) появилось в математике при расширении множества натуральных чисел. Цель расширения: обеспечить выполнение операции вычитания для любых чисел. В результате расширения получается множество (кольцо) целых чисел, состоящее из положительных (натуральных) чисел, отрицательных чисел и нуля.

Все отрицательные числа, и только они, меньше, чем нуль. На числовой оси отрицательные числа располагаются слева от нуля. Для них, как и для положительных чисел, определено отношение порядка, позволяющее сравнивать одно целое число с другим.

Для каждого натурального числа n существует одно и только одно отрицательное число, обозначаемое -n, которое дополняет n до нуля: n + ( − n) = 0. Оба числа называются противоположными друг для друга. Вычитание целого числа a равносильно сложению с противоположным для него: -a.

Содержание

Свойства отрицательных чисел

Отрицательные числа подчиняются практически тем же правилам, что и натуральные, но имеют некоторые особенности.

  1. Если любое множество положительных чисел ограничено снизу, то любое множество отрицательных чисел ограничено сверху.
  2. При умножении целых чисел действует правило знаков: произведение чисел с разными знаками отрицательно, с одинаковыми — положительно.
  3. При умножении обеих частей неравенства на отрицательное число знак неравенства меняется на обратный. Например, умножая неравенство 3 < 5 на -2, мы получаем: -6 > −10.
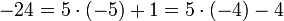  4. При делении с остатком частное может иметь любой знак, но остаток, по соглашению, всегда неотрицателен (иначе он определяется не однозначно). Например, разделим −24 на 5 с остатком: -24 = 5 \cdot (-5) + 1 = 5 \cdot (-4) - 4 .

Исторический очерк

Древний Египет, Вавилон и Древняя Греция не использовали отрицательных чисел, а если получались отрицательные корни уравнений (при вычитании), они отвергались как невозможные.

Впервые отрицательные числа были частично узаконены в Китае, а затем (примерно с VII века) и в Индии, где трактовались как долги (недостача), или признавались как промежуточный этап, полезный для вычисления окончательного, положительного результата. Правда, умножение и деление для отрицательных чисел тогда ещё не были определены.

Диофант в III веке уже знал правило знаков и умел умножать отрицательные числа. Однако и он рассматривал их лишь как временные значения.

Полезность и законность отрицательных чисел утверждались постепенно. Индийский математики Брахмагупта (VII век) уже рассматривал их наравне с положительными. В Европе признание наступило на тысячу лет позже, да и то долгое время отрицательные числа называли «ложными», «мнимыми» или «абсурдными». Даже Паскаль считал, что 0 − 4 = 0, так как ничто не может быть меньше, чем ничто. Бомбелли и Жирар, напротив, считали отрицательные числа вполне допустимыми и полезными, в частности, для обозначения недостачи чего-либо. Отголоском тех времён является то обстоятельство, что в современной арифметике операция вычитания и знак отрицательных чисел обозначаются одним и тем же символом (минус), хотя алгебраически это совершенно разные понятия.

В XVII веке, с появлением аналитической геометрии, отрицательные числа получили наглядное геометрическое представление на числовой оси. С этого момента наступает их полное равноправие. Тем не менее теория отрицательных чисел долго находилась в стадии становления. Оживлённо обсуждалась, например, странная пропорция 1:(-1) = (-1):1 — в ней первый член слева больше второго, а справа — наоборот, и получается, что большее равно меньшему («парадокс Арно»). Непонятно было также, какой смысл имеет умножение отрицательных чисел, и почему произведение отрицательных положительно; на эту тему проходили жаркие дискуссии.

Полная и вполне строгая теория отрицательных чисел была создана только в XIX веке (Уильям Гамильтон и Герман Грассман).

Литература

См. также

Ссылки

Wikimedia Foundation.2010.