Парадокс дня рождения | это... Что такое Парадокс дня рождения? (original) (raw)

Парадо́кс дней рожде́ния — утверждение, что если дана группа из 23 или более человек, то вероятность того, что хотя бы у двух из них дни рождения (число и месяц) совпадут, превышает 50 %. Для группы из 60 или более человек вероятность совпадения дней рождения хотя бы у двух её членов составляет более 99 %, хотя 100 % она достигает, только когда в группе не менее 366 человек (с учётом високосных лет — 367).

Такое утверждение может показаться противоречащим здравому смыслу, так как вероятность одному родиться в определённый день года довольно мала, а вероятность того, что двое родились в конкретный день — ещё меньше, но является верным в соответствии с теорией вероятностей. Таким образом, оно не является парадоксом в строгом научном смысле — логического противоречия в нём нет, а парадокс заключается лишь в различиях между интуитивным восприятием ситуации человеком и результатами математического расчёта.

Содержание

Интуитивное восприятие

Один из способов понять на интуитивном уровне, почему в группе из 23 человек вероятность совпадения дней рождения у двух человек столь высока, состоит в осознании следующего факта: поскольку рассматривается вероятность совпадения дней рождения у любых двух человек в группе, то эта вероятность определяется количеством пар людей, которые можно составить из 23 человек. Так как порядок людей в парах не имеет значения, то общее число таких пар равно числу сочетаний из 23 по 2, то есть 23 × 22/2 = 253 пары. Посмотрев на это число, легко понять, что при рассмотрении 253 пар людей вероятность совпадения дней рождения хотя бы у одной пары будет достаточно высокой.

Ключевым моментом здесь является то, что утверждение парадокса дней рождения говорит именно о совпадении дней рождения у каких-либо двух членов группы. Одно из распространённых заблуждений состоит в том, что этот случай путают с другим — похожим, на первый взгляд, — случаем, когда из группы выбирается один человек и оценивается вероятность того, что у кого-либо из других членов группы день рождения совпадёт с днем рождения выбранного человека. В последнем случае вероятность совпадения значительно ниже.

Расчёт вероятности

В данном примере для расчёта вероятности того, что в группе из n человек как минимум у двух дни рождения совпадут, примем, что дни рождения распределены равномерно, то есть нет високосных лет, близнецов, рождаемость не зависит от дня недели, времени года и других факторов. В действительности, это не совсем так — обычно летом рождается больше детей; кроме того, в некоторых странах из-за особенностей работы больниц больше детей рождается в определённые дни недели. Однако неравномерность распределения может лишь увеличить вероятность совпадения дней рождения, но не уменьшить: если бы все люди рождались только в 3 дня из 365, то вероятность совпадения дней рождения была бы очень высокой.

Рассчитаем сначала, какова вероятность p (n) того, что в группе из n человек дни рождения всех людей будут различными. Если n > 365, то в силу принципа Дирихле вероятность равна нулю. Если же n ≤ 365, то будем рассуждать следующим образом. Возьмём наугад одного человека из группы и запомним его день рождения. Затем возьмём наугад второго человека, при этом вероятность того, что у него день рождения не совпадёт с днем рождения первого человека, равна 1 — 1/365. Затем возьмём третьего человека, при этом вероятность того, что его день рождения не совпадёт с днями рождения первых двух, равна 1 — 2/365. Рассуждая по аналогии, мы дойдём до последнего человека, для которого вероятность несовпадения его дня рождения со всеми предыдущими будет равна 1 — (n — 1)/365. Перемножая все эти вероятности, получаем вероятность того, что все дни рождения в группе будут различными:

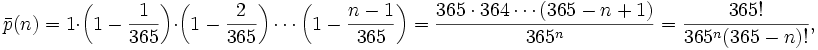
\bar p(n) = 1 \cdot \left(1-\frac{1}{365}\right) \cdot \left(1-\frac{2}{365}\right) \cdots \left(1-\frac{n-1}{365}\right) = { 365 \cdot 364 \cdots (365-n+1) \over 365^n } = { 365! \over 365^n (365-n)!},

Тогда вероятность того, что хотя бы у двух человек из n дни рождения совпадут, равна

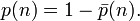
p(n) = 1 - \bar p(n) .

Значение этой функции превосходит 1/2 при n = 23 (при этом вероятность совпадения равна примерно 50.7 %). Вероятности для некоторых значений n иллюстрируются следущей таблицей:

n p (n)
10 12 %
20 41 %
30 70 %
50 97 %
100 99.99996 %
200 99.9999999999999999999999999998 %
300 (1 − 7×10−73) × 100 %
350 (1 − 3×10−131) × 100 %
366 100 %

Альтернативный метод расчёта

Вероятность совпадения дней рождения в группе можно также рассчитать с использованием формул комбинаторики. Представим, что каждый день года — это одна буква в алфавите из 365 букв. Дни рождения n человек могут быть представлены строкой, состоящей из n букв такого алфавита. Общее число таких строк равно

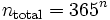
n_\mathrm{total} = 365^{n}\,

Общее число строк, в которых буквы не повторяются, составит

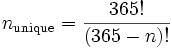
n_\mathrm{unique} = \frac{365!}{(365-n)!}

Тогда, если строки выбираются случайно (с равномерным распределением), то вероятность выбрать строку, в которой хотя бы две буквы совпадут, равна

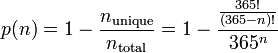
p(n) = 1 - \frac{n_\mathrm{unique}}{n_\mathrm{total}} = 1 - \frac{\frac{365!}{(365-n)!}}{365^{n}}

для n ≤ 365 и p (n) = 1 для n > 365.

Поскольку

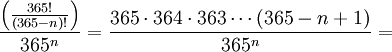
\frac{\left(\frac{365!}{(365-n)!}\right)}{365^{n}}=\frac{365\cdot 364\cdot 363 \cdots (365-n+1)}{365^{n}}=

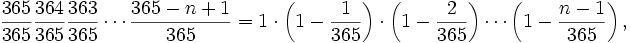
\frac{365}{365}\frac{364}{365}\frac{363}{365}\cdots \frac{365-n+1}{365}=1 \cdot \left(1-\frac{1}{365}\right) \cdot \left(1-\frac{2}{365}\right) \cdots \left(1-\frac{n-1}{365}\right) ,

то это выражение эквивалентно представленному выше.

Аппроксимации

Используя разложение экспоненциальной функции в ряд Тейлора

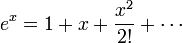
e^x = 1 + x + \frac{x^2}{2!}+\cdots

приведённое выше выражение, дающее значение p (n), можно аппроксимировать следующим образом:

График, показывающий соотношение между точным значением и аппроксимацией p (n)

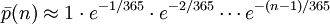
\bar p(n) \approx 1 \cdot e^{-1/365} \cdot e^{-2/365} \cdots e^{-(n-1)/365}

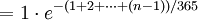
= 1 \cdot e^{-(1+2+ \cdots +(n-1))/365}

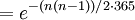
= e^{-(n(n-1))/2 \cdot 365}

Следовательно,

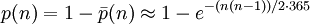
p(n) = 1-\bar p(n) \approx 1 - e^{-(n(n-1))/2 \cdot 365}

Для ещё более грубой аппроксимации можно взять выражение

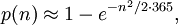
p(n)\approx 1-e^{-n^2/{2 \cdot 365}},\,

которое, как показывает график, всё ещё даёт достаточную точность.

Родившиеся в один день с заданным человеком

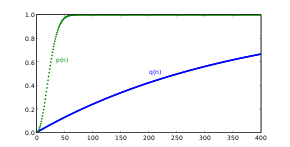
Сравнение вероятностей p (n) и q (n)

Интересно сравнить вероятность p (n) с вероятностью того, что в группе из n человек у кого-либо день рождения совпадет с днём рождения некоторого заранее выбранного человека (не принадлежащего к этой группе). Эта вероятность равна

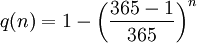
q(n) = 1 - \left( \frac{365-1}{365} \right)^n

Подставляя n = 23, получаем q (n) примерно 5.9 %, что лишь немногим лучше одного шанса из 17. Для того, чтобы вероятность совпадения дня рождения с заданным человеком превысила 50 %, число людей в группе должно быть не менее 253. Это число заметно больше, чем половина дней в году (365/2 = 182.5); так происходит из-за того, что у остальных членов группы дни рождения могут совпадать между собой, и это уменьшает вероятность совпадения одного из них с днём рождения заданного человека.

Задача в общем виде

Задача, представленная парадоксом дней рождения, может быть поставлена в общем виде следующим образом: если даны n равномерно распределённых случайных чисел в диапазоне от 1 до d, то какова вероятность p (n ; d) того, что хотя бы два из этих чисел совпадут ?

Рассуждая таким же образом, как описано выше, можно получить общие решения:

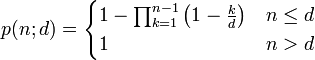
p(n;d) = \begin{cases} 1-\prod_{k=1}^{n-1}\left(1-{k \over d}\right) & n\le d \\ 1 & n > d \end{cases}

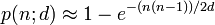
p(n;d) \approx 1 - e^{-(n(n-1))/2d}

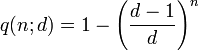
q(n;d) = 1 - \left( \frac{d-1}{d} \right)^n

Приложения

Парадокс дней рождения в общем смысле применим к хеш-функциям: если хеш-функция генерирует N_-битное значение, то число случайных входных данных, для которых хеш-коды с большой вероятностью дадут коллизию (то есть, найдутся равные хеш-коды полученные на разных входных данных), равно не 2_N, а только около 2_N_/2. Это наблюдение используется в атаке «дней рождения» на криптографические хеш-функции.

Сходный математический аппарат используется для оценки популяции рыб в озёрах методом «capture-recapture». Действительно, если каждую пойманную рыбу помечать и отпускать, то вероятность поймать помеченную рыбу будет расти нелинейно (в соответствии с приведённым выше графиком) с ростом количества попыток. Размер популяции грубо может быть оценен как квадрат числа попыток до первой помеченной пойманной рыбы.

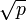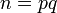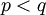Решение задачи в общем виде находит применение во многих разделах математики, например в недетерминированных алгоритмах факторизации. Так, одно из самых простых объяснений ρ-метода Полларда аналогично объяснению парадокса дней рождения: достаточно иметь примерно \sqrt{p} случайных чисел от 0 до n=p q ~, где p < q ~ — простые, чтобы хотя бы для одной из пар чисел с высокой вероятностью нашёлся 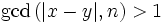\gcd \left( |x-y|,n \right) > 1, который и будет делителем числа n.

Близкие дни рождения

Другое обобщение парадокса дней рождения состоит в постановке задачи о том, сколько человек нужно для того, чтобы вероятность наличия в группе людей, дни рождения которых различаются не более чем на один день (или на два, три дня и так далее), превысила 50 %. Эта задача более сложная, при её решении используется принцип включения-исключения. Результат (опять-таки в предположении, что дни рождения распределены равномерно) получается следующим:

Максимальное различие дней рождения, дней Необходимое число людей
1 23
2 14
3 11
4 9
5 8
6 8
7 7
8 7

Таким образом, вероятность того, что даже в группе из 7 людей дни рождения хотя бы у двух будут различаться не более чем на неделю, превышает 50 %.

См. также

Ссылки

Литература

Wikimedia Foundation.2010.