Полином Эрмита | это... Что такое Полином Эрмита? (original) (raw)
Полином Эрмита
Полином Эрмита
Многочлены Эрмита — определенного вида последовательность многочленов одной вещественной переменной. Многочлены Эрмита возникают в теории вероятностей, в комбинаторике, физике.
Эти многочлены названы в честь Шарля Эрмита.
Содержание
Определение
В теории вероятностей полиномы Эрмита обычно определяются выражением:
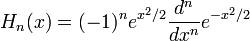 ;
;
в физике обычно используется другое определение:
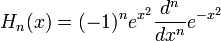 .
.
Два определения, приведенные выше, не являются в точности эквивалентными друг другу; каждое из них является "отмасштабированной" версией другого
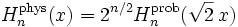 .
.
Явные выражения для первых десяти многочленов Эрмита приведены ниже (вероятностное определение):
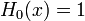
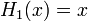
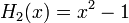
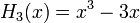
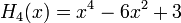
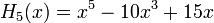
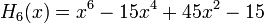
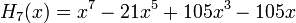
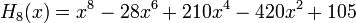
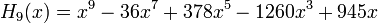
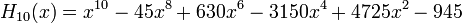 .
.
Свойства
Ортогональность
H n(x) -- полином порядка n, где n = 0, 1, 2, 3, .... Полиномы этой последовательности попарно ортогональны относительно скалярного произведения, задаваемого выражением:
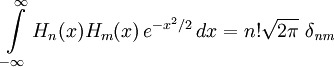 (вероятностная версия)
(вероятностная версия)
или
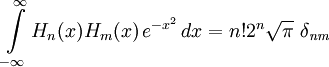 (физическая версия)
(физическая версия)
где δ_nm_ -- Символ Кронекера, по определению равный 1, когда n = m и нулю во всех остальных случаях.
Таким образом, многочлены Эрмита образуют отрогональный базис в Гильбертовом пространстве функций, ограниченных в соответствующей норме
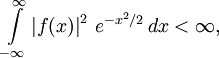 .
.
Дифференциальное уравнение Эрмита
Многочлен Эрмита _n_-го порядка удовлетворяет дифференциальному уравнению Эрмита:
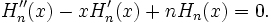 (в теории вероятностей)
(в теории вероятностей)
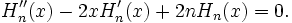 (в физике)
(в физике)
Рекурсивное выражение
Последовательность многочленов Эрмита допускает рекурсивное определение:
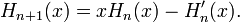 (в теории вероятностей)
(в теории вероятностей)
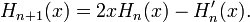 (в физике)
(в физике)
Применение
- Полиномы Эрмита применяются, в частности, в методе конечных элементов в качестве функций формы, что позволяет повысить гладкость получаемых приближенных решений.
- В квантовой механике полиномы Эрмита появляются при решении задачи квантового гармонического осциллятора
Ссылки
- Weisstein, Eric W. Hermite Polynomial на сайте Wolfram MathWorld.(англ.)
- Module for Hermite Polynomial Interpolation by John H. Mathews
Wikimedia Foundation.2010.
Полезное
Смотреть что такое "Полином Эрмита" в других словарях:
- полином Эрмита — Ermito daugianaris statusas T sritis fizika atitikmenys: angl. Hermite polynomial vok. Hermitesches Polynom, n rus. полином Эрмита, m; эрмитов полином, m pranc. polynôme d’Hermite, m … Fizikos terminų žodynas
- Полином — В математике, многочлены или полиномы от одной переменной функции вида где ci фиксированные коэффициенты, а x переменная. Многочлены составляют один из важнейших классов элементарных функций. Изучение полиномиальных уравнений и их решений… … Википедия
- эрмитов полином — Ermito daugianaris statusas T sritis fizika atitikmenys: angl. Hermite polynomial vok. Hermitesches Polynom, n rus. полином Эрмита, m; эрмитов полином, m pranc. polynôme d’Hermite, m … Fizikos terminų žodynas
- Многочлен Эрмита — Многочлены Эрмита определенного вида последовательность многочленов одной вещественной переменной. Многочлены Эрмита возникают в теории вероятностей, в комбинаторике, физике. Эти многочлены названы в честь Шарля Эрмита. Содержание 1 Определение 2 … Википедия
- Полиномы Эрмита — Многочлены Эрмита определенного вида последовательность многочленов одной вещественной переменной. Многочлены Эрмита возникают в теории вероятностей, в комбинаторике, физике. Эти многочлены названы в честь Шарля Эрмита. Содержание 1 Определение 2 … Википедия
- Сплайн Эрмита — Кубический эрмитов сплайн сплайн, построенный из кубических полиномов с использованием эрмитовой интерполяции, в соответствии с которой интерполируемая функция задается не только своими значениями в n точках, но и ее первыми производными. Для… … Википедия
- Эрмит, Шарль — Шарль Эрмит Шарль Эрмит (190 … Википедия
- Эрмит — Эрмит, Шарль Шарль Эрмит (фр. Charles Hermite; 24 декабря 1822, Дьёзе, Лотарингия, Франция 14 января 1901 … Википедия
- Ermito daugianaris — statusas T sritis fizika atitikmenys: angl. Hermite polynomial vok. Hermitesches Polynom, n rus. полином Эрмита, m; эрмитов полином, m pranc. polynôme d’Hermite, m … Fizikos terminų žodynas
- Hermite polynomial — Ermito daugianaris statusas T sritis fizika atitikmenys: angl. Hermite polynomial vok. Hermitesches Polynom, n rus. полином Эрмита, m; эрмитов полином, m pranc. polynôme d’Hermite, m … Fizikos terminų žodynas