Уравнение Гамильтона — Якоби | это... Что такое Уравнение Гамильтона — Якоби? (original) (raw)

В физике и математике, уравнение Гамильтона — Якоби

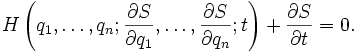
H\left(q_1,\dots,q_n;\frac{\partial S}{\partial q_1},\dots,\frac{\partial S}{\partial q_n};t\right) + \frac{\partial S}{\partial t}=0.

Здесь S обозначает классическое действие, 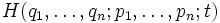H(q_1,\dots,q_n;p_1,\dots,p_n;t) — классический гамильтониан, q i — обобщенные координаты.

Непосредственно относится к классической (не квантовой) механике, однако хорошо приспособлено для установления связи между классической механикой и квантовой, так как его можно, например, получить практически прямо из уравнения Шрёдингера в приближении быстроосциллирующей волновой функции (больших частот и волновых чисел).

В классической механике возникает обычно из специального канонического преобразования классического гамильтониана, которое приводит к этому нелинейному дифференциальному уравнению первого порядка, решение которого описывает поведение динамической системы.

Следует отличать уравнение Гамильтона — Якоби от уравнений движения Гамильтона и Эйлера — Лагранжа. Хотя это уравнение и выводится из них, но представляет собой одно уравнение, описывающее динамику механической системы с любым количеством степеней свободы s, в отличие от 2_s_ уравнений Гамильтона и s уравнений Эйлера — Лагранжа.

Уравнение Гамильтона — Якоби помогает элегантно решить задачу Кеплера.

Каноническое преобразование

Уравнение Гамильтона — Якоби немедленно следует из того факта, что для любой генерирующей функции S(q,p',t) (пренебрегая индексами), уравнения движения не изменяются для H(q, p, t) и H'(q',p',t)

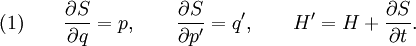
(1) \qquad {\partial S \over \partial q} = p, \qquad {\partial S \over \partial p'} = q', \qquad H' = H + {\partial S \over \partial t} .

Новые уравнения движения становятся

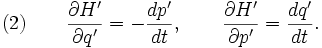
(2) \qquad {\partial H' \over \partial q'} = - {dp' \over dt}, \qquad {\partial H' \over \partial p'} = {dq' \over dt}.

Уравнение Гамильтона — Якоби появляется из специфической генерирующей функции S, которая делает H' тождественной нулю. В этом случае все его производные зануляются и

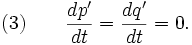
(3) \qquad {dp' \over dt} = {dq' \over dt} = 0.

Таким образом, в штрихованной системе координат, система совершенно стационарна в фазовом пространстве. Однако, мы еще не определили, при помощи какой генерирующей функции S достигается преобразование в штрихованную систему координат, таким образом мы используем тот факт что

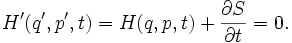
H'(q',p',t) = H(q,p,t) + {\partial S \over \partial t} = 0.

Поскольку уравнение (1) даёт 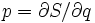p=\partial S/\partial q это можно записать

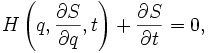
H\left(q,{\partial S \over \partial q},t\right) + {\partial S \over \partial t} = 0,

что является уравнением Гамильтона — Якоби.

Решение

Уравнение Гамильтона — Якоби часто решают методом разделения переменных. Пусть некоторая координата (для определённости будем говорить о _q_1) и соответствующий ей импульс 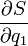\frac{\partial S}{\partial q_1} входят в уравнение в форме

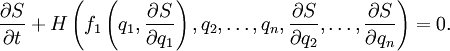
\frac{\partial S}{\partial t} + H\left( f_1 \left(q_1,\frac{\partial S}{\partial q_1}\right), q_2,\ldots,q_n,\frac{\partial S}{\partial q_2},\ldots,\frac{\partial S}{\partial q_n}\right) =0 .

Тогда можно положить

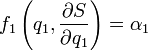
f_1 \left(q_1,\frac{\partial S}{\partial q_1}\right) = \alpha_1

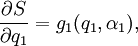
\frac{\partial S}{\partial q_1} = g_1(q_1,\alpha_1) ,

где α1 — произвольная постоянная, _g_1 — обратная функция, и решать уравнение Гамильтона — Якоби уже с меньшим числом переменных. Если процесс можно продолжить по всем переменным, то решение уравнения примет вид

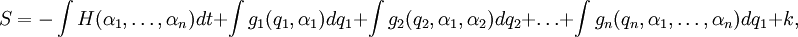
S = - \int H(\alpha_1,\ldots,\alpha_n) dt + \int g_1(q_1,\alpha_1)dq_1 + \int g_2(q_2,\alpha_1,\alpha_2)dq_2 + \ldots + \int g_n(q_n,\alpha_1,\dots,\alpha_n)dq_1 + k,

где α_i_ — произвольные постоянные, k — константа интегрирования. Напомним, что при этом S является функцией конечной точки 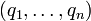(q_1,\dots,q_n). Так как действие задаёт каноническое преобразование гамильтоновой системы, то его производные по координатам — это импульсы в новой системе координат, поэтому они должны сохраняться:

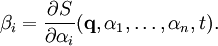
\beta_i={\partial S \over \partial \alpha_i}(\mathbf{q},\alpha_1,\dots,\alpha_n,t) .

Совместно с уравнениями на импульсы это определяет движение системы.

Литература

См. также