Распределение Накагами | это... Что такое Распределение Накагами? (original) (raw)

Распределение Накагами

Плотность вероятности 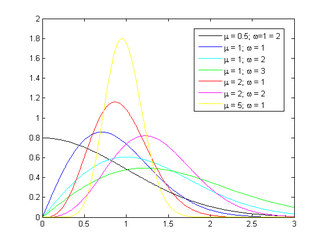Nakagami pdf.png
Функция распределения 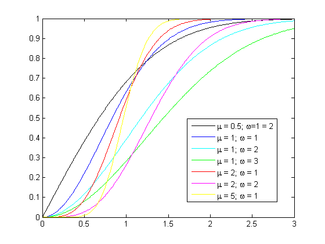Nakagami cdf.png
Обозначение {{{notation}}}
Параметры \mu >= 0.5 real) \omega > 0 (real)
Носитель x > 0\!
Плотность вероятности \frac{2\mu^\mu}{\Gamma(\mu)\omega^\mu} x^{2\mu-1} \exp\left(-\frac{\mu}{\omega}x^2 \right)
Функция распределения \frac{\gamma \left(\mu,\frac{\mu}{\omega} x^2\right)}{\Gamma(\mu)}
Математическое ожидание \frac{\Gamma(\mu+\frac{1}{2})}{\Gamma(\mu)}\left(\frac{\omega}{\mu}\right)^{1/2}
Медиана \sqrt{\omega}\!
Мода \frac{\sqrt{2}}{2} \left(\frac{(2\mu-1)\omega}{\mu}\right)^{1/2}
Дисперсия \omega\left(1-\frac{1}{\mu}\left(\frac{\Gamma(\mu+\frac{1}{2})}{\Gamma(\mu)}\right)^2\right)
Коэффициент асимметрии
Коэффициент эксцесса
Информационная энтропия
Производящая функция моментов
Характеристическая функция

Распределение Накагами или m-распределение Накагами — распределение вероятности, функция плотности вероятности которого равна[1]

f(x;\,\mu,\omega) = \frac{2\mu^\mu}{\Gamma(\mu)\omega^\mu}x^{2\mu-1}\exp\left(-\frac{\mu}{\omega}x^2\right). .

Оценка параметров

Параметры μ и ω оцениваются следующим образом[2]:

\mu = \frac{\operatorname{E}^2 \left[X^2 \right]} {\operatorname{Var} \left[X^2 \right]},

и

\omega = \operatorname{E} \left[X^2 \right].

История и применение

Распределение Накагами является относительно новым. Оно было предложено в 1960 году[3]. Используется для моделирования замираний сигналов в беспроводных многоулучёвых каналах связи[4].

Ссылки

  1. ↑ Laurenson, Dave Nakagami Distribution. Indoor Radio Channel Propagation Modelling by Ray Tracing Techniques (1994). Архивировано из первоисточника 30 сентября 2012. Проверено 4 августа 2007.
  2. ↑ R. Kolar, R. Jirik, J. Jan (2004) «Estimator Comparison of the Nakagami-m Parameter and Its Application in Echocardiography», Radioengineering, 13 (1), 8-12
  3. ↑ M. Nakagami. «The m-Distribution, a general formula of intensity of rapid fading». In William C. Hoffman, editor, Statistical Methods in Radio Wave Propagation: Proceedings of a Symposium held June 18-20, 1958, pp 3-36. Pergamon Press, 1960.
  4. ↑ J. D. Parsons, The Mobile Radio Propagation Channel. New York: Wiley, 1992.
Bvn-small.png п·Вероятностные распределения
Одномерные Многомерные
Дискретные: Бернулли | биномиальное геометрическое гипергеометрическое логарифмическое отрицательное биномиальное Пуассона дискретное равномерное мультиномиальное
Абсолютно непрерывные: Бета | Вейбулла Гамма гиперэкспоненциальное Колмогорова Коши Лапласа логнормальное нормальное (Гаусса) логистическое Накагами Парето полукруговое непрерывное равномерное Райса Рэлея Стьюдента Фишера хи-квадрат экспоненциальное variance-gamma многомерное нормальное | копула