Алгоритм Флойда — Уоршелла | это... Что такое Алгоритм Флойда — Уоршелла? (original) (raw)

Алгоритм Флойда — Уоршелла

Алгоритм Флойда — Уоршелла — динамический алгоритм для нахождения кратчайших расстояний между всеми вершинами взвешенного ориентированного графа. Разработан в 1962 году Робертом Флойдом и Стивеном Уоршеллом.

Содержание

Алгоритм

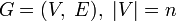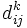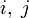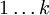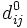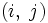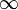Пусть вершины графа G=(V,\; E),\; |V| = n пронумерованы от 1 до n и введено обозначение d_{i j}^{k} для длины кратчайшего пути от i до j, который кроме самих вершин i,\; j проходит только через вершины 1 \ldots k. Очевидно, что d_{i j}^{0} — длина (вес) ребра (i,\;j), если таковое существует (в противном случае его длина может быть обозначена как \infty)

Существует два варианта значения 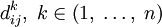d_{i j}^{k},\;k \in \mathbb (1,\;\ldots,\;n):

  1. Кратчайший путь между 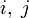i,\;j не проходит через вершину k, тогда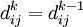 d_{i j}^{k}=d_{i j}^{k-1}
  2. Существует более короткий путь между 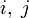i,\;j, проходящий через k, тогда он сначала идёт от i до k, а потом от k до j. В этом случае, очевидно,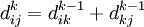 d_{i j}^{k}=d_{i k}^{k-1} + d_{k j}^{k-1}

Таким образом, для нахождения значения функции достаточно выбрать минимум из двух обозначенных значений.

Тогда рекуррентная формула для 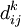d_{i j}^k имеет вид:

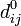d_{i j}^0 — длина ребра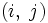 (i,\;j)

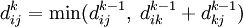
d_{i j}^{k} = \min (d_{i j}^{k-1},\; d_{i k}^{k-1} + d_{k j}^{k-1})

Алгоритм Флойда — Уоршелла последовательно вычисляет все значения 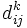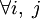d_{i j}^{k}, \forall i,\; j для k от 1 до n. Полученные значения 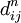d_{i j}^{n} являются длинами кратчайших путей между вершинами i,\; j.

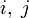Псевдокод

На каждом шаге алгоритм генерирует двумерную матрицу W, 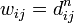w_{ij}=d_{i j}^n. Матрица W содержит длины кратчайших путей между всеми вершинами графа. Перед работой алгоритма матрица W заполняется длинами рёбер графа.

for k = 1 to n for i = 1 to n for j = 1 to n W[i][j] = min(W[i][j], W[i][k] + W[k][j])

Сложность алгоритма

Три вложенных цикла содержат операцию, исполняемую за константное время. 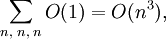\sum_{n,\;n,\;n}O(1) = O(n^3), то есть алгоритм имеет кубическую сложность, при этом простым расширением можно получить также информацию о кратчайших путях — помимо расстояния между двумя узлами записывать матрицу идентификатор первого узла в пути.

Вариации алгоритма

Построение матрицы достижимости

Алгоритм Флойда — Уоршелла может быть использован для нахождения замыкания отношения E по транзитивности. Для этого в качестве W[0] используется бинарная матрица смежности графа, 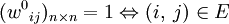({w^0}_{i j})_{n \times n} = 1 \Leftrightarrow (i,\; j) \in E; оператор min заменяется дизъюнкцией, сложение заменяется конъюнкцией:

for k = 1 to n for i = 1 to n for j = 1 to n W[i][j] = W[i][j] or (W[i][k] and W[k][j])

После выполнения алгоритма матрица W является матрицей достижимости.

Использование битовых масок при реализации алгоритма позволяет существенно ускорить алгоритм. При этом сложность алгоритма снижается до O(n_3 / log_n) (в модели вычислений RAM). На практике, еще бо́льшего ускорения можно достичь, используя такие специализированные наборы микропроцессорных команд, как SSE.

См. также

Ссылки

Литература

Wikimedia Foundation.2010.