Узел (топология) | это... Что такое Узел (топология)? (original) (raw)

Содержание

Понятие математического узла

Узлы — предметы простые и наглядные. Вы, конечно, встречались с ними в повседневной жизни, но, может быть, не подозревали, что это ещё и математические объекты; более того, в последние 20 лет математики и физики с огромным интересом и удивительной интенсивностью стали заниматься соответствующими теориями, особенно теорией узлов. Достаточно сказать, что за это время четыре медали Филдса были получены именно за работы, связанные с этой теорией. А именно, лауреатами медали Филдса в разное время стали Владимир Дринфельд из Харькова, работающий в Чикаго, Максим Концевич из Москвы, работающий в Париже, Воган Джонс из Новой Зеландии, работающий в Калифорнии, и Эдвард Виттен, физик-теоретик, работающий в Принстоне.

Чем отличается математический узел от узлов, которые завязывают на галстуках или на шнурках ботинок? Естественно, в математике узел — это некая абстракция: рассматривается не верёвка и не шнур, а бесконечно тонкая, гибкая и растяжимая нить. Кроме того, рассматривая математический узел, нужно либо как-то зафиксировать его концы (обычно говорят, что один конец уходит в бесконечность «вверх», а другой — в бесконечность «вниз», либо просто соединить их (см. рис.). В последнем случае модель узла — замкнутая несамопересекающаяся кривая в пространстве. Будем предполагать, что эта кривая является ломаной, то есть состоит из отрезков (впрочем, на рисунках мы почти всегда будем изображать узлы в виде гладких кривых, считая отдельные звенья ломаной. Самый простой узел — тривиальный (простая окружность). Узел называется нетривиальным, если он не эквивалентен тривиальному, то есть его нельзя «пошевелить» (возможно растягивая, но не разрывая верёвку) так, чтобы он превратился в тривиальный.

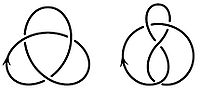
Трилистник и восьмёрка

Вот несколько примеров нетривиальных узлов: узел на рис. слева называется трилистником, узел на рис. справа — восьмёркой. (Обычно узлы рассматривают с ориентацией, то есть считают, что задано направление обхода кривой, это направление изображается стрелкой.)

Алгебра узлов

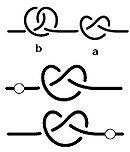
А можно ли умножать узлы? Если считать узлы кривыми, концы которых уходят в бесконечность, то умножение узлов определяется естественным образом: произведение узлов а и b — это просто нить, на которой завязан сначала узел а, затем узел b (рис. справа). Это умножение ассоциативно: для любых узлов а, b и с верно равенство: (ab)c=a(bc). Ясно, что тривиальный узел (то есть просто вертикальная прямая) является единичным элементом. Ни один нетривиальный узел не имеет обратного. Покажем, что два узла, завязанные на одной веревке, можно переставить. Действительно, пусть на нити завязан сначала узел a, затем узел b. Сперва, не трогая узел a, «затянем» узел b в маленький узелок. Потом заключим этот узелок в маленький стеклянный шарик и будем двигать его вверх по нити. В итоге этот шарик окажется наверху, и его можно превратить опять в узел b. Таким образом, умножние узлов коммутативно: ab=ba.
Итак, верна
Теорема об узлах. Узлы образуют ассоциативную и коммутативную систему относительно умножения. В этой системе есть единичный элемент, но нет обратных.

Компьютер развязывает узлы

Первый шаг в этой теории состоит в сведении (сложной) пространственной задачи развязывания узла к (более простой) задаче применения простых операций к кривым на плоскости. Эти операции придумал в 1920-е годы немецкий математик Рейдемейстер.
Имеет место
Лемма Рейдемейстера. Если узел можно развязать (превратить в окружность) в пространстве, то его плоскую диаграмму можно распутать на плоскости с помощью операций Рейдемейстера.

Некоторые типы узлов

См. также

Ссылки

Wikimedia Foundation.2010.