Проекция Меркатора | это... Что такое Проекция Меркатора? (original) (raw)

Карта мира Меркатора 1569 года

Равноугольная цилиндрическая проекция Меркатора — одна из основных картографических проекций. Разработана Герардом Меркатором для применения в его «Атласе». «Равноугольная» в названии проекции подчёркивает то, что проекция сохраняет углы между направлениями. Все локсодромы в ней изображаются прямыми линиями. Меридианы в проекции Меркатора представляются параллельными равноотстоящими линиями. Параллели же представляют собой параллельные линии, расстояние между которыми равно расстоянию между меридианами вблизи экватора и быстро увеличивается при приближении к полюсам. Сами полюсы не могут быть изображены на проекции Меркатора (это обусловлено особенностями функции, отображающей координаты на сфере на координаты на плоскости), поэтому обычно карту в проекции Меркатора ограничивают областями до 80-85° градусов северной и южной широты.

Масштаб на карте в этой проекции не является постоянным, он увеличивается от экватора к полюсам (как обратный косинус широты), однако масштабы по вертикали и по горизонтали всегда равны, чем, собственно, и достигается равноугольность проекции. На картах в данной проекции всегда указывается, к какой параллели относится основной масштаб карты.

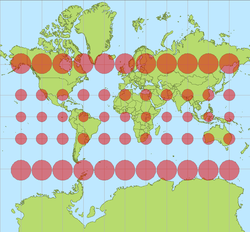
Искажения площадей в проекции Меркатора

Поскольку проекция Меркатора имеет различный масштаб на разных участках, эта проекция не сохраняет площади. Если основной масштаб относится к экватору, то наибольшие искажения размеров объектов будут у полюсов. Это хорошо заметно на картах в этой проекции: на них Гренландия кажется в 2-3 раза больше Австралии и сравнима по размерам с Южной Америкой. В реальности Гренландия втрое меньше Австралии и в 8 раз меньше Латинской Америки.

Проекция Меркатора оказалась весьма удобной для нужд мореходства, особенно в старые времена. Объясняется это тем, что траектория движения корабля, идущего под одним и тем же румбом к меридиану (т.е. с неизменным положением стрелки компаса относительно шкалы) изображается прямой линией на карте в проекции Меркатора.

Математическое выражение проекции Меркатора

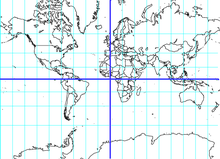
Карта мира в проекции Меркатора с координатными линиями, проведёнными через 20°.

Для начала рассмотрим простейший вариант проекции Меркатора: проекцию сферы на цилиндр. Этот вариант не учитывает сплюснутости Земли у полюсов. Цилиндричность проекции сразу даёт нам выражение для горизонтальной координаты на карте: она просто пропорциональна долготе точки $\lambda$ (при использовании в расчетах следует учесть, что выражаться эта величина должна в радианах)

$x=c(\lambda-\lambda_0)$ .

Условие равноугольности — это просто равенство масштабов по горизонтальной и вертикальной оси. Поскольку масштаб по оси X на широте $\theta$ равен просто $c/(R\cos\theta)$ (R — радиус Земли), то из условия $dy R\cos\theta/c= R d\theta$ мы получаем выражение для зависимости y от $\theta$

$\begin{matrix} y &=& c \ln\mathop{\rm tg}\left(\frac{\theta}{2}+\frac{\pi}{4}\right)\\ &=& c \,\mathop{\rm ath}\sin\theta \end{matrix}$ .

Обратное преобразование

$\begin{matrix} \theta &=& 2\mathop{\rm arctg} \left( e^{y/c} \right) - \frac{1} {2} \pi \\ \\ \ &=& \mathop{\rm arctg} \left( \mathop{\rm sh} (y/c) \right) \\ \\ \lambda &=& x/c + \lambda_0. \end{matrix}$

Теперь нетрудно получить выражения для равноугольной проекции с учётом эллипсоидальной формы Земли. Для этого надо записать метрическую форму для эллипсоида (a — большая полуось, b — меньшая) в географических координатах

$dl^2=\frac{a^2 d\lambda^2}{1+\frac{a^2}{b^2}\mathop{\rm tg}^2\theta}+\frac{b^4}{a^2}\frac{d\theta^2}{(\cos^2\theta+\frac{b^2}{a^2}\sin^2\theta)^3},$

перейти в ней к координатам x и y и приравнять масштабы по осям. После интегрирования получаем

$\begin{matrix} x &=& c(\lambda-\lambda_0)\\ y &=& c [\mathop{\rm ath}\sin\theta-\varepsilon\mathop{\rm ath}(\varepsilon\sin\theta)]. \end{matrix}$

Здесь $\varepsilon=\sqrt{a^2-b^2}/a$ — эксцентриситет земного эллипсоида. Обратное преобразование не выражается в элементарных функциях, но уравнение для обратного преобразования легко решить методом теории возмущений по малому $\epsilon$ .

Итерационная формула для обратного преобразования имеет следующий вид:

$\theta_{n+1} = f \left(\theta_{n},y\right)$ , где $\theta_0$ можно взять равным 0 или приближению, рассчитанному по формуле для сфероида.

$\theta_{n+1} = arcsin\left(1-\frac{(1+\sin \theta_n)(1-\varepsilon\sin \theta_n)^\varepsilon}{e^\frac{2y}{c}(1+\varepsilon\sin \theta_n)^\varepsilon}\right)$

Ссылки

Проекция Меркатора в учебнике по морской навигации

Знаменитые карты и глобусы
Древний мир	Туринская папирусная карта \| Вавилонская карта мира	Карта Птолемея	Пейтингерова таблица	Мадабская карта	Христианская топография
Средневековье(mappa mundi, портуланы)	Карта Т и О \| Меровингская карта	Беатова карта	Карта Рожера	Херефордская карта	Эбсторфская карта	Карты Дульсерта	Каталанский атлас	Карта Пиццигано	Карта де Вирга	Карта Бьянко	Карта фра Мауро	Карта Винланда
Великие географические открытия	Карта Хуана де ла Коса \| Планисфера Кантино	Карта де Кавери	Карта Вальдземюллера	Карта Пьетро Коппо	Карта Пири-реиса
Новое время	Carta Marina \| Leo Belgicus	Maris Pacifici	Большой Чертёж Меркаторовы карты	Атлас Ортелия	Космография Блау	План Тюрго
Дальневосточные карты	Большая карта династии Мин \| Каннидо	Карта Мао Куня	Карта Маттео Риччи
Глобусы	Земное яблоко \| Ягеллонский глобус	Глобус Иоганна Шёнера	Готторпский глобус	Глобус Блау