Закон Бернулли | это... Что такое Закон Бернулли? (original) (raw)

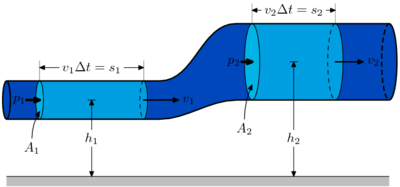
Закон Бернулли является следствием закона сохранения энергии для стационарного потока идеальной (то есть без внутреннего трения) несжимаемой жидкости:

$\tfrac{\rho v^2}{2} + \rho g h + p = \mathrm{const}$

Здесь

$~\rho$ — плотность жидкости,

— скорость потока,

— высота, на которой находится рассматриваемый элемент жидкости,

— давление в точке пространства, где расположен центр массы рассматриваемого элемента жидкости,

— ускорение свободного падения.

В научной литературе закон Бернулли, как правило, называется уравнением Бернулли[1](не следует путать с дифференциальным уравнением Бернулли), теоремой Бернулли[2][3] или интегралом Бернулли[4][5].

Константа в правой части часто называется полным давлением и зависит, в общем случае, от линии тока.

Размерность всех слагаемых — единица энергии, приходящаяся на единицу объёма жидкости. Первое и второе слагаемое в интеграле Бернулли имеют смысл кинетической и потенциальной энергии, приходящейся на единицу объёма жидкости. Следует обратить внимание на то, что третье слагаемое по своему происхождению является работой сил давления (см. приводимый в приложении вывод уравнения Бернулли) и не представляет собой запаса какого-либо специального вида энергии («энергии давления»[6]).

Соотношение, близкое[7] к приведенному выше, было получено в 1738 г. Даниилом Бернулли, с именем которого обычно связывают интеграл Бернулли. В современном виде интеграл был получен Иоганном Бернулли около 1740 года.

Для горизонтальной трубы h=0 и уравнение Бернулли принимает вид: $\tfrac{\rho v^2}{2}+p=\mathrm{const}$ .

Эта форма уравнения Бернулли может быть получена путём интегрирования уравнения Эйлера для стационарного одномерного потока жидкости, при постоянной плотности $\rho$ : $v\tfrac{dv}{dx}=-\tfrac {1}{\rho}\cdot \tfrac {dp}{dx}$ .

Согласно закону Бернулли, полное давление в установившемся потоке жидкости остается постоянным вдоль этого потока.

Полное давление состоит из весового $(\rho g h)$ , статического (p) и динамического $\left(\tfrac{\rho v^2}{2}\right)$ давлений.

Из закона Бернулли следует, что при уменьшении сечения потока, из-за возрастания скорости, то есть динамического давления, статическое давление падает. Это является основной причиной эффекта Магнуса. Закон Бернулли справедлив и для ламинарных потоков газа. Явление понижения давления при увеличении скорости потока лежит в основе работы различного рода расходомеров (например труба Вентури), водо- и пароструйных насосов. А последовательное применение закона Бернулли привело к появлению технической гидромеханической дисциплины — гидравлики.

Закон Бернулли справедлив в чистом виде только для жидкостей, вязкость которых равна нулю. Для описания течений реальных жидкостей в технической гидромеханике (гидравлике) используют интеграл Бернулли с добавлением слагаемых, учитывающих потери на местных и распределенных сопротивлениях.

Одно из применений

Закон Бернулли можно применить к истечению идеальной несжимаемой жидкости через малое отверстие в боковой стенке или дне широкого сосуда.

Закон Бернулли позволяет объяснить эффект Вентури: в узкой части трубы скорость течения жидкости выше, а давление меньше, чем на участке трубы большего диаметра, в результате чего наблюдается разница высот столбов жидкости $\Delta h$ ; бо́льшая часть этого перепада давлений обусловлена изменением скорости течения жидкости, и может быть вычислена по уравнению Бернулли

Согласно закону Бернулли приравняем полные давления на верхней поверхности жидкости и на выходе из отверстия:

$\rho g h + p_0 = \frac{\rho v^2}{2} + p_0$ ,

где

p_0 — атмосферное давление,

— высота столба жидкости в сосуде,

— скорость истечения жидкости,

$z\, +\, \frac{p}{\rho g}$ — гидростатический напор (сумма геометрического напора z и пьезометрической высоты $\frac{p}{\rho g}$ ).

Отсюда: $v = \sqrt{2gh}$ . Это — формула Торричелли. Она показывает, что при истечении идеальной несжимаемой жидкости из отверстия в широком сосуде жидкость приобретает скорость, какую получило бы тело, свободно падающее с высоты .

Часто уравнение Бернулли записывается в виде:

$Hd\, =\, z\, +\, \frac{p}{\rho g}\, +\, \frac{v^2}{2\,g}=\, \text{const}\,$

где

$Hd\,$ — гидродинамический напор,

$\frac{v^2}{2\,g}$ — скоростной напор.

Для сжимаемого идеального газа

$\frac {v^2}{2}+ gh+\left(\frac {\gamma}{\gamma-1}\right)\frac {p}{\rho} = \mathrm{const}$ [8] (постоянна вдоль линии тока или линии вихря)

где

$\gamma = \frac{C_p}{C_V}$ — Адиабатическая постоянная газа

— давление газа в точке

$\rho$ — плотность газа в точке

— скорость течения газа

— ускорение свободного падения

— высота относительно начала координат

При движении в неоднородном поле заменяется на потенциал гравитационного поля.

Термодинамика закона Бернулли

Из статистической физики следует, что на линиях тока при адиабатическом течении остается постоянным следующее соотношение:

$\frac{v^2}{2} + w + \varphi = \mathrm{const}$

где — энтальпия единицы массы, $\varphi$ — потенциал силы.

Вывод закона Бернулли из уравнения Эйлера и термодинамических соотношений

1. Запишем Уравнение Эйлера:

$\rho \frac{\partial \vec v}{\partial t} + \rho (\vec v, \nabla) \vec v = - \nabla p - \rho \nabla \varphi$

$\varphi$ — потенциал. Для силы тяжести $\varphi = gz$

2. Запишем выражение для энтальпии и предположим, что энтропия системы постоянна (или, можно сказать, что течение адиабатично):

dW = V dP + T dS

Пусть S=const и — энтальпия единицы массы, тогда:

$dw = \frac{dp}{\rho}$

или

$\nabla w = \frac{\nabla p}{\rho}$

3. Воспользуемся следующими соотношениями из векторной алгебры:

$\frac 12 \nabla v^2 = (\vec v, \nabla) \vec v + \vec v \times \operatorname{rot}\vec v$

$\vec l \cdot \nabla = \frac{\partial}{\partial l}$ — проекция градиента на некоторое направление равно производной по этому направлению.

4. Уравнение Эйлера с использованием соотношений выведенных выше:

$\rho \frac{\partial \vec v}{\partial t} + \rho \left[ \frac 12 \nabla v^2 - \vec v \times \operatorname{rot}\vec v \right] = - \rho \nabla (\varphi + w)$

Спроецируем это уравнение на единичный вектор касательный к линии тока, учитывая следующее:

$\frac{\partial \vec v}{\partial t} = 0$ — условие стационарности

$(\vec l , \vec v \times \operatorname{rot}\vec v ) = 0$ — так как $\vec l ||\vec v$

Получаем:

$\frac{\partial}{\partial l} \left( \frac{v^2}{2} + w + \varphi \right) = 0$

То есть на линиях тока в стационарной адиабатической жидкости выполняется следующее соотношение:

$\frac{v^2}{2} + w + \varphi = \operatorname{const}$

Практические следствия

закон Бернулли объясняет эффект притяжения между телами, находящимися вблизи границ потоков движущихся жидкостей (газов). Иногда это притяжение может создавать угрозу безопасности. Например, при движении скоростного поезда «Сапсан» (скорость движения более 200 км/час) для людей на платформах возникает опасность сброса под поезд.[9] Аналогично «затягивающая сила» возникает при движении судов параллельным курсом: например, подобные инциденты происходили с лайнером «Олимпик».
Автоаварии: проносящиеся мимо многотонные грузовики с прицепами притягиваются к стоящему на обочине автобана автомобилю. Это одна из опасностей, которыми объясняют запрет на остановку автомобилей на обочинах автобанов.

Приложение

Вывод уравнения Бернулли

Энергия маленького элемента жидкости: $E=\frac{mv^2}2+U$ (U - потенциальная энергия)

Слева на большой объем жидкости между двумя поверхностями действует сила $p_1\cdot S_1$ , а справа - $-p_2\cdot S_2$ (минус, потому что влево).

Итак, этот объем жидкости сдвинулся (за время ). Пусть его левая граница сдвинулась на dl_1 , а правая - на dl_2 .

Пишем условие несжимаемости: $S_1\cdot dl_1=V_1=V_2=S_2\cdot dl_2$ . Объёмы, как видно, бесконечно малые, дифференциальные. Их самих можно рассматривать как дифференциалы объёма всего большого элемента.

Далее. Сначала наш большой элемент состоял из левого голубого элемента и средней синей части. Теперь он состоит из средней синей части и правого голубого элемента. При этом все его молекулы сдвинулись, но так как течение стационарное, то в каждой точке со временем энергия не меняется. Поэтому энергия средней синей части не поменялась. Поэтому работа сил (ну, или за бесконечно малое время не сама работа, а её дифференциал) равна изменению энергии, равному, в свою очередь, энергии правого голубого элементика (который добавился) минус энергия левого голубого элементика (который, наоборот, ушёл, влился в средний синий). $p_1\cdot S_1\cdot dl_1 - p_2\cdot S_2\cdot dl_2 = dA = E_2-E_1 = \frac{m_2\cdot v_2^2}2+U_2-\frac{m_1\cdot v_1^2}2-U_1 = \frac{\rho V_2v_2^2}2+U_2-\frac{\rho V_1v_1^2}2-U_1$ .

Теперь вспоминаем формулу несжимаемости и сокращаем на объём. $p_1-p_2 = \frac{\rho v_2^2}2-\frac{\rho v_1^2}2+{U_2\over V_2}-{U_1\over V_1}$ .

Сгруппируя слагаемые, получаем формулу Бернулли: $p_1+{U_1\over V_1}+\frac{\rho v_1^2}2 = p_2+{U_2\over V_2}+\frac{\rho v_2^2}2$ , или просто $p+\frac UV+\frac{\rho v^2}2=const$ , или, подставив потенциальную энергию, $p+\rho gh+\frac{\rho v^2}2=const$ .

См. также

Даниил Бернулли
Закон Дарси
Интеграл Лагранжа — Коши

Литература

Ландау, Л. Д., Лифшиц, Е. М. Гидродинамика. — Издание 5-е.. — М., 2003. — 736 с. — («Теоретическая физика», том VI). — ISBN 5-9221-0121-8

Ссылки

Примечания

↑ Титьенс О., Прандтль Л. Гидро- и аэромеханика. — М.-Л.: ГТТИ, 1933. — Т. 1. — 224 с.
↑ Лойцянский Л.Г. Механика жидкости и газа. — М.: Дрофа, 2003. — 842 с. — ISBN 5-7107-6327-6
↑ Милн-Томсон Л.М. Теоретическая гидродинамика. — М.: Мир, 1964. — 656 с.
↑ Седов Л.И. Механика сплошной среды. — М.: Наука, 1970. — Т. 2. — 568 с.
↑ Чёрный Г.Г. Газовая динамика. — М.: Наука, 1988. — 424 с. — ISBN 5-02-013814-2
↑ Чугаев Р.Р. Гидравлика. — Л.: Энергия, 1975. — 600 с.
↑ В частности, в записи Д.Бернулли в явном виде не фигурировало давление, см. Трусделл К. Очерки по истории механики. — М.-Ижевск: Институт компьютерных исследований, 2002. — 316 с. — ISBN 5-93972-192-3
↑ Clancy, L.J., Aerodynamics, Section 3.11
↑ Валерий Панкрашин Камни для „Сапсана“, или „месть бедных“. Би-Би-Си (26 марта 2010). Архивировано из первоисточника 5 февраля 2012.