Большая окружность | это... Что такое Большая окружность? (original) (raw)

Большая окружность

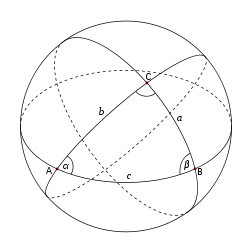
Сферический треугольник

Сферическая геометрия — раздел геометрии, изучающий геометрические фигуры на поверхности сферы. Сферическая геометрия возникла в древности в связи с потребностями географии и астрономии.

Основные понятия

Через любые две точки на поверхности сферы (кроме диаметрально противоположных) можно провести единственный большой круг — окружность, образованную пересечением сферы и плоскости, проходящей через её центр. Большие круги на поверхности сферы играют роль, аналогичную роли прямых в планиметрии. Любые два больших круга пересекаются в двух диаметрально противоположных точках.

При пересечении двух больших кругов образуются четыре сферических двуугольника. Площадь двуугольника определяется формулой S = 2_R_2α, где R — радиус сферы, а α — угол двуугольника.

Три больших круга, не пересекающихся в одной точке, образуют восемь сферических треугольников. Сферический треугольник, все стороны которого меньше половины большого круга, называется эйлеровым. Помимо трёх признаков равенства плоских треугольников, для сферических треугольников имеет место ещё один: два сферических треугольника равны, если их соответствующие углы равны.

Стороны сферического треугольника измеряют величиной угла, образованного радиусами сферы, проведёнными к концам данной стороны. Каждая сторона сферического треугольника меньше суммы и больше разности двух других. Сумма всех сторон сферического треугольника всегда меньше 2π. Сумма углов сферического треугольника s = α + β + γ всегда меньше 3π и больше π. Величина 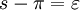$s-\pi = \varepsilon$ называется сферическим избытком. 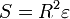Площадь сферического треугольника определяется по формуле Жирара $S=R^2 \varepsilon$ .

Соотношения между элементами сферического треугольника изучает сферическая тригонометрия

Вариации и обобщения

См. Геометрия Римана

Литература

Алексеевский Д. В., Винберг Э. Б., Солодовников А. С. Геометрия пространств постоянной кривизны. В кн.: Итоги науки и техники. Современные проблемы математики. Фундаментальные направления. М.: ВИНИТИ, 1988. Т. 29. С. 1-146.
Берже М. Геометрия. Пер. с франц., в 2 т. М.: Мир, 1984. Том II, часть V: Внутренняя геометрия сферы, гиперболическая геометрия, пространство сфер.
Степанов Н. Н. Сферическая тригонометрия. Л.-М., 1948.

См. также

Wikimedia Foundation.2010.

Полезное

Смотреть что такое "Большая окружность" в других словарях:

Намёт мозжечка — Твёрдая мозговая оболочка и ее отростки. Намёт мозжечка показан зелёным У этого термина существуют и другие значения, см. Намёт (значения). Намёт мозжечка (палатка мозжечка … Википедия
НОВОРОЖДЕННЫЙ — НОВОРОЖДЕННЫЙ, ребенок в течение двух трех недель с момента рождения. В это время происходит приспособление его к внеутробной жизни, отпадает и заживает пуповина, служившая связью между ним и матерью, и выравниваются последствия родовой травмы.… … Большая медицинская энциклопедия
МОРСА ПЕРЕСТРОЙКА — хирургия, преобразование гладких многообразий, к рому подвергается многообразие уровня гладкой функции при переходе через невырожденную критическую точку;важнейшая конструкция в топологии многообразий. Пусть V гладкое п мерное многообразие (без… … Математическая энциклопедия
Хирургия (топология) — Хирургия или перестройка Морса преобразование гладких многообразий, которому подвергается многообразие уровня гладкой функции при переходе через невырожденную критическую точку; важнейшая конструкция в дифференциальной топологии. Конструкция… … Википедия
Перестройка Морса — Хирургия или перестройка Морса преобразование гладких многообразий, которому подвергается многообразие уровня гладкой функции при переходе через невырожденную критическую точку; важнейшая конструкция в дифференциальной топологии. Важная… … Википедия
ГОРОПТЕР — ГОРОПТЕР, поверхность в поле зрения, все точки к рой дают изображения в парных идентичных точках сетчатки и потому не дают двойных образов. Лучи от точек, лежащих вне Г., дают всегда двойные изображения, т. к. падают на диспаратные места сетчатки … Большая медицинская энциклопедия
Гренландия — большая земля, находящаяся на крайнем СВ Америки, на атлантической ее стороне. Имея вытянутую с С на Ю форму и достигая на юге 60° сев. шир., Г. заходит на севере за 83°. Ее крайние пункты на В приходятся приблизительно под 19°, а крайние… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
КОНСТИТУЦИЯ — КОНСТИТУЦИЯ. (от лат. constitutio состояние, сложение, свойство), качества организма, телосложение и т. п., гл. обр. те свойства индивидуума, которые влияют на возникновение и течение б ней. К конституции человека издавна причисляют также его… … Большая медицинская энциклопедия
РОДЫ — РОДЫ. Содержание: I. Определение понятия. Изменения в организме во время Р. Причины наступления Р..................... 109 II. Клиническое течение физиологических Р. . 132 Ш. Механика Р. ................. 152 IV. Ведение Р.................. 169 V … Большая медицинская энциклопедия
Москва* — первопрестольная стол. России. История. Первое летописное слово о М. относится к 1147 г., когда суздальский князь Юрий Долгорукий в этой своей вотчинной усадьбе давал сильный обед пир своему союзнику и другу северскому князю Святославу Ольговичу… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона