Джон Валлис | это... Что такое Джон Валлис? (original) (raw)

Джон Валлис

Джон Валлис (John Wallis; 23 ноября (3 декабря) 1616 — 28 октября (8 ноября) 1703) — английский математик, один из предшественников математического анализа.

Валлис — сын священника из Кента. Уже в молодости вызывал восхищение как феноменальный счётчик: как-то в уме извлёк квадратный корень из 53-значного числа. Однако никакого математического образования он не получил, занимаясь самостоятельно.

По окончании Кембриджского университета (1632—1640) стал священником англиканской церкви и получив степень магистра. После женитьбы (1645) вынужден был покинуть университет, так как от профессоров в те годы требовался обет безбрачия.

В революцию прославился расшифровкой перехваченных писем сторонников короля. Однако он выступил против казни короля Карла I. Репутация выдающегося математика, заслуженная Валлисом к тому времени, привела к тому, что в 1649 году его пригласили в Оксфорд занять освободившуюся там (после изгнания нескольких роялистов) кафедру геометрии, которую Валлис занимал до кончины в 1703 году.

После реставрации монархии (1660) завоевал доверие нового короля, Карла II, который назначил его придворным священником.

Валлис участвовал в создании (1660) Лондонского Королевского общества — британской Академии наук — и стал одним из первых его членов.

В честь Валлиса назван астероид 31982 Джонваллис.

Научные достижения

Джон Валлис

Валлис получил значительные результаты в зарождавшемся тогда математическом анализе, геометрии, тригонометрии, теории чисел.

В 1655 году Валлис издаёт большой трактат «Арифметика бесконечного» («Arithmetica infinilorum, sive nova methodus inquirendi curvilineorum quadratura»), где появляется придуманный им символ бесконечности: ∞. В книге он формулирует строгое определение предела переменной величины, продолжает многие идеи Декарта, впервые ввёл отрицательные абсциссы, вычисляет суммы бесконечных рядов — по существу интегральные суммы, хотя понятия интеграла тогда ещё не было.

Там же приводится знаменитая «формула Валлиса»:

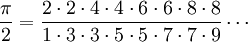
\frac{\pi}{2} = \frac{2\cdot2\cdot4\cdot4\cdot6\cdot6\cdot8\cdot8}{1\cdot3\cdot3\cdot5\cdot5\cdot7\cdot7\cdot9}\cdots

В «Трактате о конических сечениях», приложении к «Арифметике бесконечного», Валлис развил «метод неделимых» Кавальери, перенеся его на с геометрической базы на алгебраическую. Здесь он также, в современной терминологии, вычисляет ряд определённых интегралов для степенной функции и близких к ней функций. Начиная с Валлиса, конические сечения рассматриваются как плоские кривые; при этом Валлис использует не только декартовы, но и косоугольные координаты.

В математике Валлис всегда уделял особое внимание практически-вычислительным аспектам, зачастую пренебрегая строгими доказательствами. В 1685 году он опубликовал «Трактат по алгебре» с обстоятельной теорией логарифмов, разложения бинома и приближённых вычислений. Впервые появляются термины: мантисса, интерпретация, непрерывная дробь, интерполяция. Валлис вывел рекуррентные соотношения для подходящих дробей непрерывной дроби. Полную теорию этих дробей дал Эйлер в XVIII веке.

Труды Валлиса произвели большое впечатление на молодого Ньютона. Не удивительно, что именно в письмах к Валлису Ньютон впервые открыто формулирует принципы своей версии дифференциального исчисления (1692). Валлис опубликовал эти письма в переиздании своего «Трактате по алгебре» (1693).

Валлис первый дал современное определение логарифмирования — как операции, обратной возведению в степень. Непер, изобретатель логарифмов, определил их кинематически, затушевав их истинную природу.

1693 год: Валлис в своей работе воспроизводит перевод сочинения Насир ад-Дина ат-Туси о пятом постулате и предлагает эквивалентную, но более очевидную формулировку этой аксиомы: существуют подобные, но не равные фигуры.

Одновременно с Гюйгенсом и Реном он решил вопрос об упругом соударении шаров, опираясь на закон сохранения количества движения.

Из прочих работ Валлиса замечательны исследования по определению длины дуги некоторых кривых. Он сумел, на пари с Паскалем, найти длину дуги части циклоиды, её площадь и положение центра масс сегмента циклоиды.

Валлис, кроме того, писал трактаты о логике, об английской грамматике, о способе обучения глухонемых разговору и множество сочинений богословского и философского содержания.

Литература

Wikimedia Foundation.2010.