Динамическая вязкость | это... Что такое Динамическая вязкость? (original) (raw)

Механика сплошных сред
Сплошная среда Классическая механика Закон сохранения массы · Закон сохранения импульса Теория упругости Напряжение · Тензор · Твёрдые тела · Упругость · Пластичность · Закон Гука · Реология · Вязкоэластичность Гидродинамика Жидкость · Гидростатика · Гидродинамика · Вязкость · Ньютоновская жидкость · Неньютоновская жидкость · Поверхностное натяжение Основные уравнения Уравнение непрерывности · Уравнение Эйлера · Уравнения Навье — Стокса · Уравнение диффузии · Закон Гука Известные учёные Ньютон · Гук Бернулли · Эйлер · Коши · Стокс · Навье

Вя́зкость (вну́треннее тре́ние) — одно из трёх явлений переноса, свойство текучих тел (жидкостей и газов) оказывать сопротивление перемещению одной их части относительно другой. Вязкость твёрдых тел обладает рядом специфических особенностей и рассматривается обычно отдельно.

Различают динамическую вязкость (единицы измерения: пуаз, Па·с) и кинематическую вязкость (единицы измерения: стокс, м²/с, внесистемная единица — градус Энглера). Кинематическая вязкость может быть получена как отношение динамической вязкости к плотности вещества и своим происхождением обязана классическим методам измерения вязкости, таким как измерение времени вытекания заданного объема через калиброванное отверстие под действием силы тяжести.

Прибор для измерения вязкости называется вискозиметром.

Содержание

Вязкость газов

В кинетической теории газов коэффициент внутреннего трения вычисляется по формуле

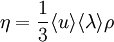\eta=\frac{1}{3}\langle u \rangle \langle\lambda \rangle \rho,

где 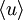\langle u \rangle — средняя скорость теплового движения молекул, λ − средняя длина свободного пробега.

Вторая вязкость

Вторая вязкость — внутреннее трение при переносе импульса в направлении движения. Влияет только при учёте сжимаемости и/или при учёте неоднородности коэффициента второй вязкости по пространству.

Вязкость жидкостей

Внутреннее трение жидкостей, как и газов, возникает при движении жидкости вследствие переноса импульса в направлении, перпендикулярном к направлению движения. Общий закон внутреннего трения — закон Ньютона: 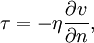\tau = - \eta \frac{\partial v}{\partial n}, Коэффициент вязкости η может быть получен на основе соображений о движениях молекул. Очевидно, что η будет тем меньше, чем меньше время t «оседлости» молекул. Эти соображения приводят к выражению для коэффициента вязкости, называемому уравнением Френкеля-Андраде: η = C e w / k T

Иная формула, представляющая коэффициент вязкости, была предложена Бачинским. Как показано, коэффициент вязкости определяется межмолекулярными силами, зависящими от среднего расстояния между молекулами; последнее определяется молярным объёмом вещества V M. Многочисленные эксперименты показали, что между молярным объёмом и коэффициентом вязкости существует соотношение 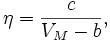\eta = \frac{c}{V_{M}-b}, где с и b — константы. Это эмпирическое соотношение называется формулой Бачинского.

Ньютоновские и неньютоновские жидкости

Ньютоновскими называют жидкости, для которых вязкость не зависит от скорости деформации. Если вязкость падает при увеличении скорости, жидкость называется тиксотропной. Для неньютоновских жидкостей методика измерения вязкости получает первостепенное значение.

Вязкость аморфных материалов

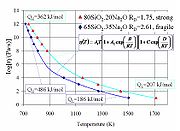
Вязкость аморфных материалов (например, стекла или расплавов), это термически активизируемый процесс[1]:

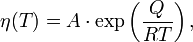
\eta(T)=A\cdot\exp\left(\frac{Q}{R T}\right),

где Q — энергия активации вязкости (кДж/моль), T — температура (К), R — универсальная газовая постоянная (8,31 Дж/моль•К) и A — некоторая постоянная.

Вязкое течение в аморфных материалах характеризуется отклонением от закона Аррениуса: энергия активации вязкости Q изменяется от большой величины Q H при низких температурах (в стеклообразном состоянии) на малую величину Q L при высоких температурах (в жидкообразном состоянии). В зависимости от этого изменения аморфные материалы классифицируются либо как сильные, когда 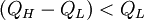\left(Q_H - Q_L\right)&amp;lt;Q_L, или ломкие, когда 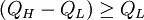\left(Q_H - Q_L\right)\geq Q_L. 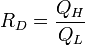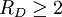Ломкость аморфных материалов численно характеризуется параметром ломкости Доримуса R_D=\frac{Q_H}{Q_L}: сильные материалы имеют R D < 2, в то время как ломкие материалы имеют R_D\ge 2.

Вязкость аморфных материалов весьма точно аппроксимируется двуэкспоненциальным уравнением:

\eta(T)=A_1\cdot T\cdot \left[1+A_2\cdot\exp\frac{B}{R T}\right]\cdot\left[1+C\exp\frac{D}{R T}\right]

с постоянными _A_1, _A_2, B, C и D, связанными с термодинамическими параметрами соединительных связей аморфных материалов.

В узких температурных интервалах недалеко от температуры стеклования T g это уравнение аппроксимируется формулами типа VTF или сжатыми экспонентами Кольрауша.

Вязкость

Если температура существенно ниже температуры стеклования T < T g, двуэкспоненциальное уравнение вязкости сводится к уравнению типа Аррениуса

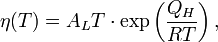
\eta(T)=A_LT\cdot\exp\left(\frac{Q_H}{R T}\right),

с высокой энергией активации Q H = H d + H m, где H d — энтальпия разрыва соединительных связей, то есть создания конфигуронов, а H m — энтальпия их движения. Это связано с тем, что при T < T g аморфные материалы находятся в стеклообразном состоянии и имеют подавляющее большинство соединительных связей неразрушенными.

При T > > T g двуэкспоненциальное уравнение вязкости также сводится к уравнению типа Аррениуса

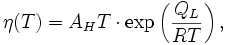
\eta(T)=A_HT\cdot\exp\left(\frac{Q_L}{R T}\right),

но с низкой энергией активации Q L = H m. Это связано с тем, что при 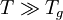T\gg T_g аморфные материалы находятся в расправленном состоянии и имеют подавляющее большинство соединительных связей разрушенными, что облегчает текучесть материала.

Сила вязкого трения

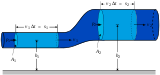
Сила вязкого трения пропорциональна скорости относительного движения V тел, пропорциональна площади S и обратно пропорциональна расстоянию между плоскостями h.

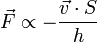
\vec{F}\propto -\frac{\vec{v} \cdot S}{h}

Коэффициент пропорциональности, зависящий от сорта жидкости или газа, называют коэффициентом динамической вязкости. Самое важное в характере сил вязкого трения то, что тела придут в движение при наличии сколь угодно малой силы, то есть не существует трения покоя. Это отличает вязкое трение от сухого.

Примечания

  1. ↑ Я. И. Френкель. Кинетическая теория жидкостей. Ленинград, Наука, 1975.

См. также

Ссылки

Литература

Wikimedia Foundation.2010.