Интеграл Бернулли | это... Что такое Интеграл Бернулли? (original) (raw)

Закон Бернулли является следствием закона сохранения энергии для стационарного потока идеальной (то есть без внутреннего трения) несжимаемой жидкости:

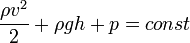
$\frac{\rho v^2}{2} + \rho g h + p = const$

Здесь

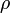$~\rho$ — плотность жидкости,

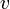— скорость потока,

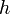— высота, на которой находится рассматриваемый элемент жидкости,

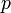— давление,

— ускорение силы тяжести.

Константа в правой части обычно называется напором, или полным давлением, а также интегралом Бернулли. Размерность всех слагаемых — единица энергии, приходящейся на единицу объёма жидкости.

Это соотношение, выведенное Даниилом Бернулли в 1738 г., было названо в его честь уравнением Бернулли. (Не путать с дифференциальным уравнением Бернулли.)

Для горизонтальной трубы h = 0 и уравнение Бернулли принимает вид: 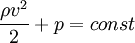$\frac{\rho v^2}{2}+p=const$ .

Эта форма уравнения Бернулли может быть получена путём интегрирования уравнения Эйлера для стационарного одномерного потока жидкости, при постоянной плотности ρ: 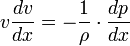$v\frac{dv}{dx}=-\frac {1}{\rho}\cdot \frac {dp}{dx}$ .

Согласно закону Бернулли полное давление в установившемся потоке жидкости остается постоянным вдоль этого потока.

Полное давление состоит из весового (ρ_g_ h), статического (p) и динамического (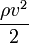 $\frac{\rho v^2}{2}$ ) давлений.

Из закона Бернулли следует, что при уменьшении сечения потока, из-за возрастания скорости, то есть динамического давления, статическое давление падает. Это является основной причиной эффекта Магнуса. Закон Бернулли справедлив и для ламинарных потоков газа. Явление понижения давления при увеличении скорости потока лежит в основе работы различного рода расходомеров (например труба Вентури), водо- и пароструйных насосов.

Закон Бернулли справедлив в чистом виде только для жидкостей, вязкость которых равна нулю, то есть таких жидкостей, которые не прилипают к поверхности трубы. На самом деле экспериментально установлено, что скорость жидкости на поверхности твердого тела всегда в точности равна нулю.

Одно из применений

Закон Бернулли можно применить к истечению идеальной несжимаемой жидкости через малое отверстие в боковой стенке или дне широкого сосуда.

Согласно закону Бернулли приравняем полные давления на верхней поверхности жидкости и на выходе из отверстия:

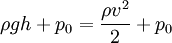$\rho g h + p_0 = \frac{\rho v^2}{2} + p_0$ ,

где

_p_0 — атмосферное давление,

h — высота столба жидкости в сосуде,

v — скорость истечения жидкости.

Отсюда: 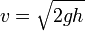$v = \sqrt{2gh}$ . Это — формула Торричелли (англ.). Она показывает, что при истечении идеальной несжимаемой жидкости из отверстия в широком сосуде жидкость приобретает скорость, какую получило бы тело, свободно падающее с высоты h.

Для сжимаемого идеального газа

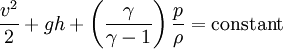$\frac {v^2}{2}+ gh+\left(\frac {\gamma}{\gamma-1}\right)\frac {p}{\rho} = \mathrm{constant}$ [1] (постоянна вдоль линии тока или линии вихря)

где

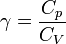$\gamma = \frac{C_p}{C_V}$ — Адиабатическая постоянная газа

p — давление газа в точке

ρ — плотность газа в точке

v — скорость течения газа

g — ускорение свободного падения

h — высота относительно начала координат

При движении в неоднородном поле g z заменяется на потенциал гравитационного поля.

Термодинамика закона Бернулли

Из статистической физики следует, что на линиях тока при адиабитическом течении остается постоянным следующее соотношение:

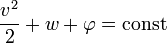
$\frac{v^2}{2} + w + \varphi = \operatorname{const}$

где w — энтальпия единицы массы, $\varphi$ — потенциал силы.

Вывод закона Бернулли из уравнения Эйлера и термодинамических соотношений

1. Запишем Уравнение Эйлера:

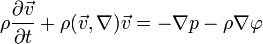
$\rho \frac{\partial \vec v}{\partial t} + \rho (\vec v, \nabla) \vec v = - \nabla p - \rho \nabla \varphi$

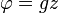
$\varphi$ — потенциал. Для силы тяжести $\varphi = gz$

2. Запишем выражение для энтальпии и предположим, что энтропия системы постоянна (или, можно сказать, что течение адиабатично):

d W = V d P + T d S

Пусть S = c o n s t и w — энтальпия единицы массы, тогда:

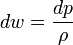
$dw = \frac{dp}{\rho}$

или

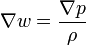
$\nabla w = \frac{\nabla p}{\rho}$

3. Воспользуемся следующими соотношениями из векторной алгебры:

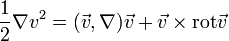
$\frac 12 \nabla v^2 = (\vec v, \nabla) \vec v + \vec v \times \operatorname{rot}\vec v$

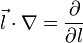$\vec l \cdot \nabla = \frac{\partial}{\partial l}$ — проекция градиента на некоторое направление равно производной по этому направлению.

4. Уравнение Эйлера с использованием соотношений выведенных выше:

$\rho \frac{\partial \vec v}{\partial t} + \rho \left[ \frac 12 \nabla v^2 - \vec v \times \operatorname{rot}\vec v \right] = - \rho \nabla (\varphi + w)$

Спроецируем это уравнение на единичный вектор касательный к линии тока, учитывая следующее:

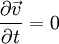$\frac{\partial \vec v}{\partial t} = 0$ — условие стационарности

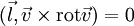$(\vec l , \vec v \times \operatorname{rot}\vec v ) = 0$ — так как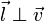 $\vec l \perp \vec v$

Получаем:

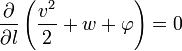
$\frac{\partial}{\partial l} \left( \frac{v^2}{2} + w + \varphi \right) = 0$

То есть на линиях тока в стационарной адиабатической жидкости выполняется следующее соотношение:

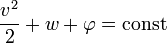
$\frac{v^2}{2} + w + \varphi = \operatorname{const}$

Приложение

Вывод уравнения Бернулли

Энергия маленького элемента жидкости: 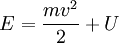$E=\frac{mv^2}2+U$ (U - потенциальная энергия)

Слева на большой объем жидкости между двумя поверхностями действует сила 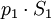$p_1\cdot S_1$ , а справа - 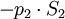$-p_2\cdot S_2$ (минус, потому что влево).

Итак, этот объем жидкости сдвинулся (за время d t). Пусть его левая граница сдвинулась на d _l_1, а правая - на d _l_2.

Пишем условие несжимаемости: 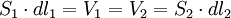$S_1\cdot dl_1=V_1=V_2=S_2\cdot dl_2$ . Объёмы, как видно, бесконечно малые, дифференциальные. Их самих можно рассматривать как дифференциалы объёма всего большого элемента.

Далее. Сначала наш большой элемент состоял из левого голубого элемента и средней синей части. Теперь он состоит из средней синей части и правого голубого элемента. При этом все его молекулы сдвинулись, но так как течение стационарное, то в каждой точке со временем энергия не меняется. Поэтому энергия средней синей части не поменялась. Поэтому работа сил (ну, или за бесконечно малое время не сама работа, а её дифференциал) равна изменению энергии, равному, в свою очередь, энергии правого голубого элементика (который добавился) минус энергия левого голубого элементика (который, наоборот, ушёл, влился в средний синий). 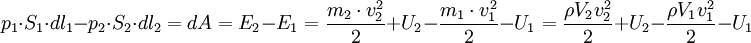$p_1\cdot S_1\cdot dl_1 - p_2\cdot S_2\cdot dl_2 = dA = E_2-E_1 = \frac{m_2\cdot v_2^2}2+U_2-\frac{m_1\cdot v_1^2}2-U_1 = \frac{\rho V_2v_2^2}2+U_2-\frac{\rho V_1v_1^2}2-U_1$ .

Теперь вспоминаем формулу несжимаемости и сокращаем на объём. 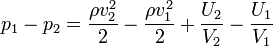$p_1-p_2 = \frac{\rho v_2^2}2-\frac{\rho v_1^2}2+{U_2\over V_2}-{U_1\over V_1}$ .

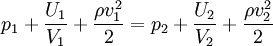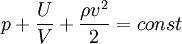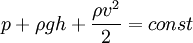Сгруппируя слагаемые, получаем формулу Бернулли: $p_1+{U_1\over V_1}+\frac{\rho v_1^2}2 = p_2+{U_2\over V_2}+\frac{\rho v_2^2}2$ , или просто $p+\frac UV+\frac{\rho v^2}2=const$ , или, подставив потенциальную энергию, $p+\rho gh+\frac{\rho v^2}2=const$ .

См. также

Даниил Бернулли

Литература

Ландау, Л. Д., Лифшиц, Е. М. Гидродинамика. — Издание 5-е.. — М.: 2003. — 736 с. — («Теоретическая физика», том VI). — ISBN 5-9221-0121-8

Примечания

↑ Clancy, L.J., Aerodynamics, Section 3.11

Wikimedia Foundation.2010.
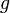