Исчисление высказываний | это... Что такое Исчисление высказываний? (original) (raw)

Логика высказываний (или пропозициональная логика) — это формальная теория, основным объектом которой служит понятие логического высказывания. С точки зрения выразительности, её можно охарактеризовать как классическую логику нулевого порядка. Логика высказываний является простейшей логикой, максимально близкой к человеческой логике неформальных рассуждений и известна ещё со времён античности.

Содержание

1 Основные понятия
2 Соглашения о скобках
3 Истинностное значение
4 Тождественно истинные формулы (тавтологии)
5 Исчисление высказываний
6 См. также
7 Ссылки

Основные понятия

Базовыми понятиями логики высказываний являются пропозициональная переменная — переменная, значением которой может быть логическое высказывание, — и (пропозициональная) формула, определяемая индуктивно следующим образом:

Если P — пропозициональная переменная, то P — формула.
Если A — формула, то 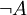$\neg A$ — формула.
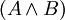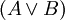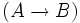Если A и B — формулы, то $(A \wedge B)$ , $(A \vee B)$ и $(A \to B)$ — формулы.
Каждая формула может быть получена за конечное число шагов при помощи предыдущих трёх правил.

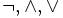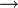Знаки $\neg, \wedge, \vee$ и $\to$ (отрицание, конъюнкция, дизъюнкция и импликация) называются пропозициональными связками. Подформулой называется часть формулы, сама являющаяся формулой. Собственной подформулой называется подформула, не совпадающая со всей формулой.

Соглашения о скобках

Поскольку в построенных по определению формулах оказывается слишком много скобок, иногда и не обязательных для однозначного понимания формулы, математики приняли соглашения о скобках, по которым некоторые из скобок можно опускать. Записи с опущенными скобками восстанавливаются так:

Когда говорят о длине формулы, имеют в виду длину подразумеваемой (восстанавливаемой) формулы, а не сокращённой записи.

Например: запись 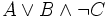$A \vee B \wedge \neg C$ означает формулу 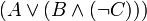$(A \vee (B \wedge ( \neg C)))$ , а её длина равна 12.

Истинностное значение

Оценкой пропозициональных переменных называется функция из множества всех пропозициональных переменных в множество {0, 1} (т.е. множество истинностных значений). Основной задачей логики высказываний является установление истинностного значения формулы, если дана оценка (т.е. определены истинностные значения входящих в неё переменных). Истинностное значение формулы в таком случае определяется индуктивно (с шагами, которые использовались при построении формулы) с использованием таблиц истинности связок.

Оценка отрицания 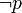$\neg p$ задаётся таблицей:

$p\!$	$\neg p$
$0\!$	$1\!$
$1\!$	$0\!$

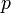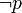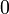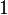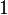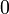Значение двуместных логических связок 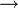$\rightarrow$ (импликация), 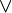$\vee$ (дизъюнкция) и 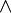$\wedge$ (конъюнкция) определются так:

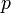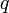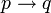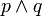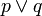$p\!$	$q\!$	$p\rightarrow q$	$p \wedge q$	$p \vee q$
0	0	1	0	0
0	1	1	0	1
1	0	0	0	1
1	1	1	1	1

Тождественно истинные формулы (тавтологии)

Формула является тождественно истинной, если она истинна при любых значениях входящих в неё переменных. Вот несколько широко известных примеров тождественно истинных формул логики высказываний:

Законы де Моргана:

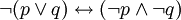$\neg (p \vee q) \leftrightarrow (\neg p \wedge \neg q)$ ;
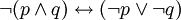$\neg (p \wedge q) \leftrightarrow (\neg p \vee \neg q)$ ;

Закон контрапозиции:

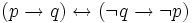$(p\rightarrow q)\leftrightarrow(\neg q\rightarrow \neg p)$ ;

Законы поглощения:

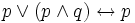$p\vee(p\wedge q)\leftrightarrow p$ ;
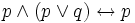$p\wedge(p\vee q)\leftrightarrow p$ ;

Законы дистрибутивности:

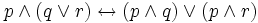$p\wedge(q\vee r)\leftrightarrow(p\wedge q)\vee(p \wedge r)$ ;
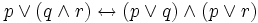$p\vee(q\wedge r)\leftrightarrow(p\vee q)\wedge(p \vee r)$ .

Исчисление высказываний

Одним из возможных вариантов (Гильбертовской) аксиоматизации логики высказываний является следующая система аксиом:

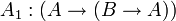$A_1 : (A \rightarrow (B \rightarrow A))$ ;

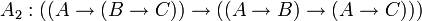$A_2 : ((A \rightarrow (B \rightarrow C)) \rightarrow ((A \rightarrow B) \rightarrow (A \rightarrow C)))$ ;

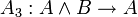$A_3 : A \wedge B \rightarrow A$ ;

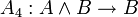$A_4 : A \wedge B \rightarrow B$ ;

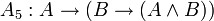$A_5 : A \rightarrow (B \rightarrow (A \wedge B))$ ;

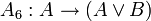$A_6 : A \rightarrow (A \vee B)$ ;

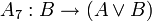$A_7 : B \rightarrow (A \vee B)$ ;

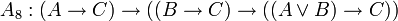$A_8 : (A \rightarrow C) \rightarrow ((B \rightarrow C) \rightarrow ((A \vee B) \rightarrow C))$ ;

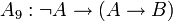$A_9 : \neg A \rightarrow (A \rightarrow B)$ ;

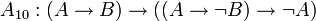$A_{10} : (A \rightarrow B) \rightarrow ((A \rightarrow \neg B)\rightarrow \neg A)$ ;

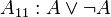$A_{11} : A\vee\neg A$ .

вместе с единственным правилом:

$\frac{A \rightarrow B, A}{B}$ (Modus ponens)

Теорема корректности исчисления высказываний утверждает, что все перечисленные выше аксиомы являются тавтологиями, а с помощью правила modus ponens из истинных высказываний можно получить только истинные. Доказательство этой теоремы тривиально и сводится к непосредственной проверке. Куда более интересен тот факт, что все остальные тавтологии можно получить из аксиом с помощью правила вывода — это так называемая теорема полноты логики высказываний.

См. также

Ссылки

Логика высказываний.

Wikimedia Foundation.2010.
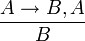