numpy.polyint — NumPy v1.13 Manual (original) (raw)

numpy. polyint(p, m=1, k=None)[source]¶

Return an antiderivative (indefinite integral) of a polynomial.

The returned order m antiderivative P of polynomial p satisfies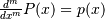 $\frac{d^m}{dx^m}P(x) = p(x)$ and is defined up to _m - 1_integration constants k. The constants determine the low-order polynomial part

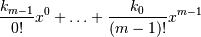
$\frac{k_{m-1}}{0!} x^0 + \ldots + \frac{k_0}{(m-1)!}x^{m-1}$

of P so that $P^{(j)}(0) = k_{m-j-1}$ .

Parameters:

p : array_like or poly1d Polynomial to differentiate. A sequence is interpreted as polynomial coefficients, see poly1d. m : int, optional Order of the antiderivative. (Default: 1) k : list of m scalars or scalar, optional Integration constants. They are given in the order of integration: those corresponding to highest-order terms come first. If None (default), all constants are assumed to be zero. If m = 1, a single scalar can be given instead of a list.

Examples

The defining property of the antiderivative:

p = np.poly1d([1,1,1]) P = np.polyint(p) P poly1d([ 0.33333333, 0.5 , 1. , 0. ]) np.polyder(P) == p True

The integration constants default to zero, but can be specified:

P = np.polyint(p, 3) P(0) 0.0 np.polyder(P)(0) 0.0 np.polyder(P, 2)(0) 0.0 P = np.polyint(p, 3, k=[6,5,3]) P poly1d([ 0.01666667, 0.04166667, 0.16666667, 3. , 5. , 3. ])

Note that 3 = 6 / 2!, and that the constants are given in the order of integrations. Constant of the highest-order polynomial term comes first:

np.polyder(P, 2)(0) 6.0 np.polyder(P, 1)(0) 5.0 P(0) 3.0