spalde — SciPy v1.15.3 Manual (original) (raw)

scipy.interpolate.

scipy.interpolate.spalde(x, tck)[source]#

Evaluate a B-spline and all its derivatives at one point (or set of points) up to order k (the degree of the spline), being 0 the spline itself.

Legacy

This function is considered legacy and will no longer receive updates. While we currently have no plans to remove it, we recommend that new code uses more modern alternatives instead. Specifically, we recommend constructing a BSpline object and evaluate its derivative in a loop or a list comprehension.

Parameters:

xarray_like

A point or a set of points at which to evaluate the derivatives. Note that t(k) <= x <= t(n-k+1) must hold for each x.

tcktuple

A tuple (t,c,k) containing the vector of knots, the B-spline coefficients, and the degree of the spline whose derivatives to compute.

Returns:

results{ndarray, list of ndarrays}

An array (or a list of arrays) containing all derivatives up to order k inclusive for each point x, being the first element the spline itself.

References

[1]

de Boor C : On calculating with b-splines, J. Approximation Theory 6 (1972) 50-62.

[2]

Cox M.G. : The numerical evaluation of b-splines, J. Inst. Maths applics 10 (1972) 134-149.

[3]

Dierckx P. : Curve and surface fitting with splines, Monographs on Numerical Analysis, Oxford University Press, 1993.

Examples

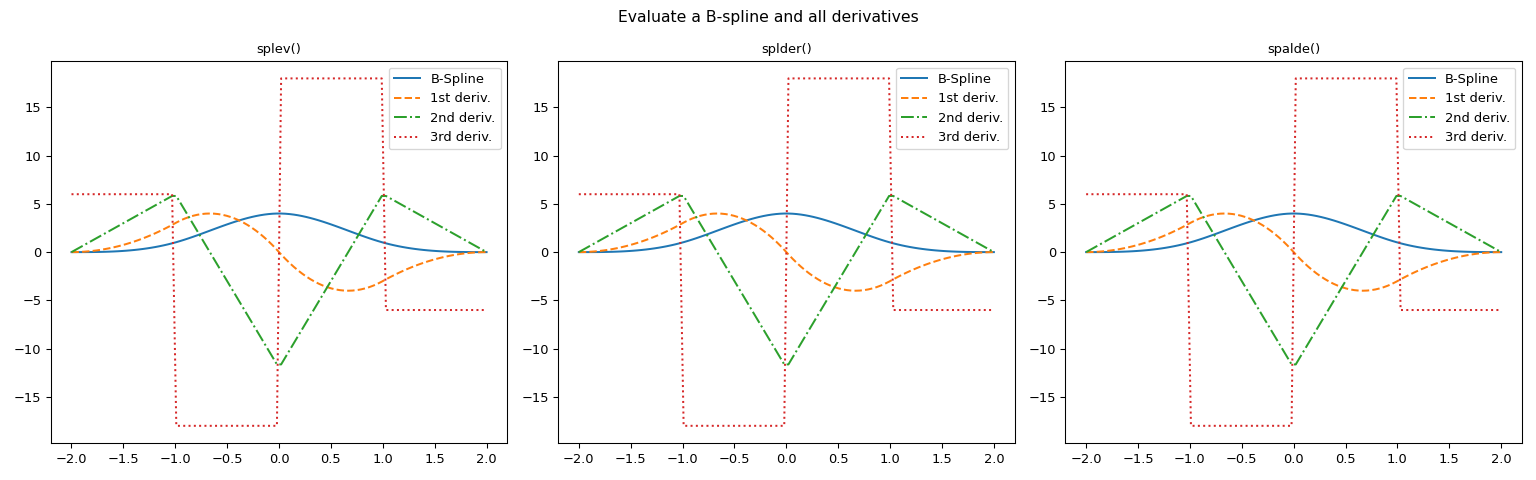
To calculate the derivatives of a B-spline there are several aproaches. In this example, we will demonstrate that spalde is equivalent to calling splev and splder.

import numpy as np import matplotlib.pyplot as plt from scipy.interpolate import BSpline, spalde, splder, splev

Store characteristic parameters of a B-spline

tck = ((-2, -2, -2, -2, -1, 0, 1, 2, 2, 2, 2), # knots ... (0, 0, 0, 6, 0, 0, 0), # coefficients ... 3) # degree (cubic)

Instance a B-spline object

BSpline objects are preferred, except for spalde()

bspl = BSpline(tck[0], tck[1], tck[2])

Generate extra points to get a smooth curve

x = np.linspace(min(tck[0]), max(tck[0]), 100)

Evaluate the curve and all derivatives

The order of derivative must be less or equal to k, the degree of the spline

Method 1: spalde()

f1_y_bsplin = [spalde(i, tck)[0] for i in x ] # The B-spline itself f1_y_deriv1 = [spalde(i, tck)[1] for i in x ] # 1st derivative f1_y_deriv2 = [spalde(i, tck)[2] for i in x ] # 2nd derivative f1_y_deriv3 = [spalde(i, tck)[3] for i in x ] # 3rd derivative

You can reach the same result by using splevand splder

f2_y_deriv3 = splev(x, bspl, der=3) f3_y_deriv3 = splder(bspl, n=3)(x)

Generate a figure with three axes for graphic comparison

fig, (ax1, ax2, ax3) = plt.subplots(1, 3, figsize=(16, 5)) suptitle = fig.suptitle(f'Evaluate a B-spline and all derivatives')

Plot B-spline and all derivatives using the three methods

orders = range(4) linetypes = ['-', '--', '-.', ':'] labels = ['B-Spline', '1st deriv.', '2nd deriv.', '3rd deriv.'] functions = ['splev()', 'splder()', 'spalde()'] for order, linetype, label in zip(orders, linetypes, labels): ... ax1.plot(x, splev(x, bspl, der=order), linetype, label=label) ... ax2.plot(x, splder(bspl, n=order)(x), linetype, label=label) ... ax3.plot(x, [spalde(i, tck)[order] for i in x], linetype, label=label) for ax, function in zip((ax1, ax2, ax3), functions): ... ax.set_title(function) ... ax.legend() plt.tight_layout() plt.show()