jn_zeros — SciPy v1.15.3 Manual (original) (raw)

scipy.special.

scipy.special.jn_zeros(n, nt)[source]#

Compute zeros of integer-order Bessel functions Jn.

Compute nt zeros of the Bessel functions \(J_n(x)\) on the interval \((0, \infty)\). The zeros are returned in ascending order. Note that this interval excludes the zero at \(x = 0\)that exists for \(n > 0\).

Parameters:

nint

Order of Bessel function

ntint

Number of zeros to return

Returns:

ndarray

First nt zeros of the Bessel function.

See also

jv

Real-order Bessel functions of the first kind

jnp_zeros

Zeros of \(Jn'\)

References

Examples

Compute the first four positive roots of \(J_3\).

from scipy.special import jn_zeros jn_zeros(3, 4) array([ 6.3801619 , 9.76102313, 13.01520072, 16.22346616])

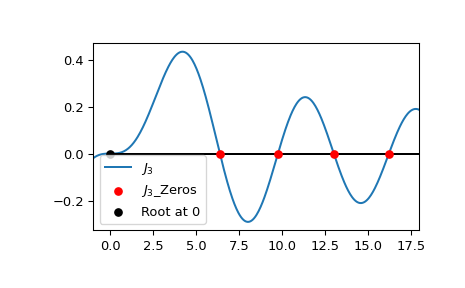
Plot \(J_3\) and its first four positive roots. Note that the root located at 0 is not returned by jn_zeros.

import numpy as np import matplotlib.pyplot as plt from scipy.special import jn, jn_zeros j3_roots = jn_zeros(3, 4) xmax = 18 xmin = -1 x = np.linspace(xmin, xmax, 500) fig, ax = plt.subplots() ax.plot(x, jn(3, x), label=r'$J_3$') ax.scatter(j3_roots, np.zeros((4, )), s=30, c='r', ... label=r"$J_3$_Zeros", zorder=5) ax.scatter(0, 0, s=30, c='k', ... label=r"Root at 0", zorder=5) ax.hlines(0, 0, xmax, color='k') ax.set_xlim(xmin, xmax) plt.legend() plt.show()