jvp — SciPy v1.15.2 Manual (original) (raw)

scipy.special.

scipy.special.jvp(v, z, n=1)[source]#

Compute derivatives of Bessel functions of the first kind.

Compute the nth derivative of the Bessel function Jv with respect to z.

Parameters:

varray_like or float

Order of Bessel function

zcomplex

Argument at which to evaluate the derivative; can be real or complex.

nint, default 1

Order of derivative. For 0 returns the Bessel function jv itself.

Returns:

scalar or ndarray

Values of the derivative of the Bessel function.

Notes

The derivative is computed using the relation DLFM 10.6.7 [2].

References

Examples

Compute the Bessel function of the first kind of order 0 and its first two derivatives at 1.

from scipy.special import jvp jvp(0, 1, 0), jvp(0, 1, 1), jvp(0, 1, 2) (0.7651976865579666, -0.44005058574493355, -0.3251471008130331)

Compute the first derivative of the Bessel function of the first kind for several orders at 1 by providing an array for v.

jvp([0, 1, 2], 1, 1) array([-0.44005059, 0.3251471 , 0.21024362])

Compute the first derivative of the Bessel function of the first kind of order 0 at several points by providing an array for z.

import numpy as np points = np.array([0., 1.5, 3.]) jvp(0, points, 1) array([-0. , -0.55793651, -0.33905896])

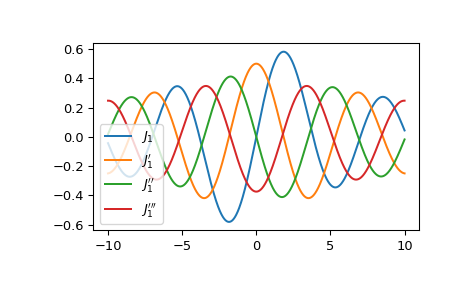
Plot the Bessel function of the first kind of order 1 and its first three derivatives.

import matplotlib.pyplot as plt x = np.linspace(-10, 10, 1000) fig, ax = plt.subplots() ax.plot(x, jvp(1, x, 0), label=r"$J_1$") ax.plot(x, jvp(1, x, 1), label=r"$J_1'$") ax.plot(x, jvp(1, x, 2), label=r"$J_1''$") ax.plot(x, jvp(1, x, 3), label=r"$J_1'''$") plt.legend() plt.show()