scipy.special.kv — SciPy v1.15.3 Manual (original) (raw)

scipy.special.kv(v, z, out=None) = <ufunc 'kv'>#

Modified Bessel function of the second kind of real order v

Returns the modified Bessel function of the second kind for real order_v_ at complex z.

These are also sometimes called functions of the third kind, Basset functions, or Macdonald functions. They are defined as those solutions of the modified Bessel equation for which,

\[K_v(x) \sim \sqrt{\pi/(2x)} \exp(-x)\]

as \(x \to \infty\) [3].

Parameters:

varray_like of float

Order of Bessel functions

zarray_like of complex

Argument at which to evaluate the Bessel functions

outndarray, optional

Optional output array for the function results

Returns:

scalar or ndarray

The results. Note that input must be of complex type to get complex output, e.g. kv(3, -2+0j) instead of kv(3, -2).

See also

kve

This function with leading exponential behavior stripped off.

kvp

Derivative of this function

Notes

Wrapper for AMOS [1] routine zbesk. For a discussion of the algorithm used, see [2] and the references therein.

References

[1]

Donald E. Amos, “AMOS, A Portable Package for Bessel Functions of a Complex Argument and Nonnegative Order”,http://netlib.org/amos/

[2]

Donald E. Amos, “Algorithm 644: A portable package for Bessel functions of a complex argument and nonnegative order”, ACM TOMS Vol. 12 Issue 3, Sept. 1986, p. 265

Examples

Plot the function of several orders for real input:

import numpy as np from scipy.special import kv import matplotlib.pyplot as plt x = np.linspace(0, 5, 1000) for N in np.linspace(0, 6, 5): ... plt.plot(x, kv(N, x), label='$K_{{{}}}(x)$'.format(N)) plt.ylim(0, 10) plt.legend() plt.title(r'Modified Bessel function of the second kind Kν(x)K_\nu(x)Kν​(x)') plt.show()

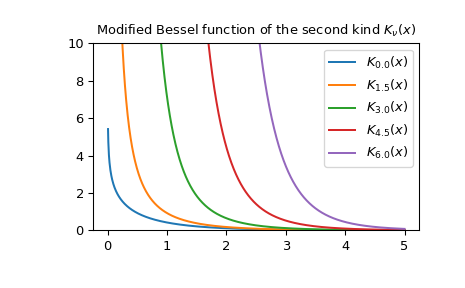
Calculate for a single value at multiple orders:

kv([4, 4.5, 5], 1+2j) array([ 0.1992+2.3892j, 2.3493+3.6j , 7.2827+3.8104j])