kvp — SciPy v1.15.2 Manual (original) (raw)

scipy.special.

scipy.special.kvp(v, z, n=1)[source]#

Compute derivatives of real-order modified Bessel function Kv(z)

Kv(z) is the modified Bessel function of the second kind. Derivative is calculated with respect to z.

Parameters:

varray_like of float

Order of Bessel function

zarray_like of complex

Argument at which to evaluate the derivative

nint, default 1

Order of derivative. For 0 returns the Bessel function kv itself.

Returns:

outndarray

The results

Notes

The derivative is computed using the relation DLFM 10.29.5 [2].

References

Examples

Compute the modified bessel function of the second kind of order 0 and its first two derivatives at 1.

from scipy.special import kvp kvp(0, 1, 0), kvp(0, 1, 1), kvp(0, 1, 2) (0.42102443824070834, -0.6019072301972346, 1.0229316684379428)

Compute the first derivative of the modified Bessel function of the second kind for several orders at 1 by providing an array for v.

kvp([0, 1, 2], 1, 1) array([-0.60190723, -1.02293167, -3.85158503])

Compute the first derivative of the modified Bessel function of the second kind of order 0 at several points by providing an array for z.

import numpy as np points = np.array([0.5, 1.5, 3.]) kvp(0, points, 1) array([-1.65644112, -0.2773878 , -0.04015643])

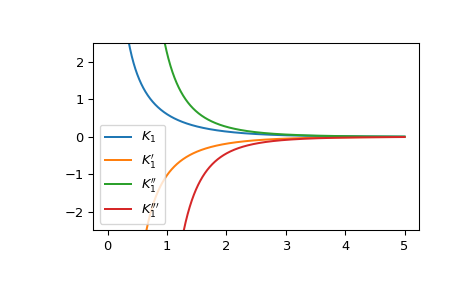
Plot the modified bessel function of the second kind and its first three derivatives.

import matplotlib.pyplot as plt x = np.linspace(0, 5, 1000) fig, ax = plt.subplots() ax.plot(x, kvp(1, x, 0), label=r"$K_1$") ax.plot(x, kvp(1, x, 1), label=r"$K_1'$") ax.plot(x, kvp(1, x, 2), label=r"$K_1''$") ax.plot(x, kvp(1, x, 3), label=r"$K_1'''$") ax.set_ylim(-2.5, 2.5) plt.legend() plt.show()