General size matrix/vector multiplication (original) (raw)

next up previous contents
Next: General size matrix/matrix multiplication Up: General size matrices Previous: Rescaling a general size Contents

General size matrix/vector multiplication

The general size matrix/vector multiplication, with optional implicit transpose of the matrix, computes one of the operations

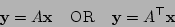
\begin{displaymath}{\bf y}= A{\bf x}\;\;\;\;\mbox{OR} \;\;\;\;{\bf y}= A^{\top}{\bf x} \end{displaymath}

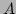for vectors ${\bf x}$, ${\bf y}$ and matrix $A$. They are implemented in Gandalf as follows.

  Gan_Matrix mA; /* matrix A */
  Gan_Vector vx, vy; /* vectors x & y */

  /* ... create and fill matrix A and vector x, create (and optionally
         fill) vector y ... */
  gan_mat_multv_q ( &mA, &vx, &vy ); /* set y = A*x, OR */
  gan_matT_multv_q ( &mA, &vx, &vy ); /* set y = A^T*x */

with the alternative forms

  Gan_Matrix mA; /* matrix A */
  Gan_Vector vx, *pvy; /* vectors x & y */

  /* ... create and fill matrix A and vector x ... */
  pvy = gan_mat_multv_s ( &mA, &vx ); /* set y = A*x, y a new vector, OR */
  pvy = gan_matT_multv_s ( &mA, &vx ); /* set y = A^T*x, y a new vector */

If 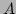$A$ is a special square matrix, more options are available. If 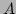$A$ is a triangular matrix, multiplication with a vector can be implemented as an in-place operation, whether or not 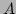$A$ is (implicitly) inverted or transposed, in any combination. This gives rise to the following Gandalf routines.

  Gan_SquMatrix smA; /* matrix A */
  Gan_Vector vx, vy; /* vectors x & y */

  /* ... create and fill matrix A and vector x, create (and optionally
         fill) vector y ... */
  gan_squmat_multv_q ( &smA, &vx, &vy ); /* set y = A*x, OR */
  gan_squmatT_multv_q ( &smA, &vx, &vy ); /* set y = A^T*x, OR */
  gan_squmatI_multv_q ( &smA, &vx, &vy ); /* set y = A^-1*x, OR */
  gan_squmatIT_multv_q ( &smA, &vx, &vy ); /* set y = A^-T*x */

with in-place versions

  Gan_SquMatrix smA; /* matrix A */
  Gan_Vector vx; /* vector x */

  /* ... create and fill matrix A and vector x ... */
  gan_squmat_multv_i ( &smA, &vxy ); /* replace x = A*x, OR */
  gan_squmatT_multv_i ( &smA, &vx ); /* replace x = A^T*x, OR */
  gan_squmatI_multv_i ( &smA, &vx ); /* replace x = A^-1*x, OR */
  gan_squmatIT_multv_i ( &smA, &vx ); /* replace x = A^-T*x */

and also the routines to create the result vector from scratch:

  Gan_SquMatrix smA; /* matrix A */
  Gan_Vector vx, *pvy; /* vectors x & y */

  /* ... create and fill matrix A and vector x ... */
  pvy = gan_squmat_multv_s ( &smA, &vxy ); /* set y = A*x, OR */
  pvy = gan_squmatT_multv_s ( &smA, &vx ); /* set y = A^T*x, OR */
  pvy = gan_squmatI_multv_s ( &smA, &vx ); /* set y = A^-1*x, OR */
  pvy = gan_squmatIT_multv_s ( &smA, &vx ); /* set y = A^-T*x */

Note that the implicit inverse and in-place features are not available when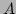$A$ is of symmetric type; Gandalf will invoke the error handler and return an error condition NULL if mA has typeGAN_SYMMETRIC_MATRIX.

Error detection: If implicit inverse is used (thegan_squmatI_multv_[qsi]() or gan_squmatIT_multv_[qsi]()routines), the matrix must be non-singular. If the matrix is singular then NULL is returned and the Gandalf error handler is invoked. Other failure modes are failing to create the result vector and incompatibility between the sizes of the input matrix and vector.

next up previous contents
Next: General size matrix/matrix multiplication Up: General size matrices Previous: Rescaling a general size Contents

2006-03-17