General size matrix/matrix multiplication (original) (raw)

Next: Inverting a general size Up: General size matrices Previous: General size matrix/vector multiplication Contents

General size matrix/matrix multiplication

Similar options are available to matrix/matrix multiplication as with matrix/vector multiplication, with the added complication that either or both if the matrices may have an implicit transpose or (for square matrices) inverse applied to them. Firstly we list the routines available when both input matrices are general rectangular matrices. In this case only implicit transpose is of relevance to us, and we can write the operations we need to implement as

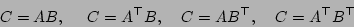
$\begin{displaymath}C = A B,\;\;\;\;\;C = A^{\top}B,\;\;\;\;C = A B^{\top},\;\;\;\;C = A^{\top}B^{\top} \end{displaymath}$

To right-multiply a matrix 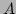$A$ by another matrix 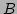$B$ , with all the above transpose combinations, the Gandalf routines are

  Gan_Matrix mA, mB, mC; /* matrices A, B & C */

  /* ... create and fill matrices A, B, create matrix C ... */
  gan_mat_rmult_q ( &mA, &mB, &mC ); /* C = A*B, OR */
  gan_mat_rmultT_q ( &mA, &mB, &mC ); /* C = A*B^T, OR */
  gan_matT_rmult_q ( &mA, &mB, &mC ); /* C = A^T*B, OR */
  gan_matT_rmultT_q ( &mA, &mB, &mC ); /* C = A^T*B^T, OR */

with similar routines to create the result matrix 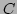$C$ from scratch:

  Gan_Matrix mA, mB, *pmC; /* matrices A, B & C */

  /* ... create and fill matrices A, B ... */
  pmC = gan_mat_rmult_s ( &mA, &mB ); /* C = A*B, OR */
  pmC = gan_mat_rmultT_s ( &mA, &mB ); /* C = A*B^T, OR */
  pmC = gan_matT_rmult_s ( &mA, &mB ); /* C = A^T*B, OR */
  pmC = gan_matT_rmultT_s ( &mA, &mB ); /* C = A^T*B^T, OR */

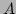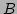The next set of routines deals with the case where it is known that the result of multiplying matrices $A$ and $B$ is symmetric. In that case we can use the routines

  Gan_Matrix mA, mB; /* matrices A & B */
  Gan_SquMatrix smC; /* matrix C */

  /* ... create and fill matrices A, B, create matrix C ... */
  gan_mat_rmult_sym_q ( &mA, &mB, &mC ); /* C = A*B, OR */
  gan_mat_rmultT_sym_q ( &mA, &mB, &mC ); /* C = A*B^T, OR */
  gan_matT_rmult_sym_q ( &mA, &mB, &mC ); /* C = A^T*B, OR */
  gan_matT_rmultT_sym_q ( &mA, &mB, &mC ); /* C = A^T*B^T */

with the alternatives

  Gan_Matrix mA, mB; /* matrices A & B */
  Gan_SquMatrix *psmC; /* matrix C */

  /* ... create and fill matrices A, B ... */
  psmC = gan_mat_rmult_sym_s ( &mA, &mB ); /* C = A*B, OR */
  psmC = gan_mat_rmultT_sym_s ( &mA, &mB ); /* C = A*B^T, OR */
  psmC = gan_matT_rmult_sym_s ( &mA, &mB ); /* C = A^T*B, OR */
  psmC = gan_matT_rmultT_sym_s ( &mA, &mB ); /* C = A^T*B^T */

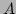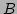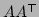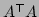In the case that $A$ and $B$ are the same matrix, we can be sure that both $AA^{\top}$ and $A^{\top}A$ are symmetric, and there are special Gandalf routines for these cases, distinguished according to whether 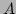$A$ is multiplied by its own transpose on the right or left:

  Gan_Matrix mA; /* matrix A */
  Gan_SquMatrix smC; /* matrix C */

  /* ... create and fill matrix A, create matrix C ... */
  gan_mat_srmultT_q ( &mA, &mC ); /* C = A*A^T, OR */
  gan_mat_slmultT_q ( &mA, &mC ); /* C = A^T*A */

with the alternatives

  Gan_Matrix mA; /* matrix A */
  Gan_SquMatrix *psmC; /* matrix C */

  /* ... create and fill matrix A ... */
  psmC = gan_mat_srmultT_s ( &mA ); /* C = A*A^T, OR */
  psmC = gan_mat_slmultT_s ( &mA ); /* C = A^T*A */

If one or both of the input matrices is a special square matrix, there are many more combinations available. First consider a square matrix 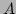$A$ being multiplied on left or right by a general rectangular matrix 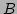$B$ , giving a result matrix 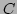$C$ . Given the possibility of both implicit transpose and inverse of the square matrix, we need to consider the operations

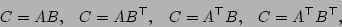
$\begin{displaymath}C = A B,\;\;\;C = A B^{\top},\;\;\;C = A^{\top}B,\;\;\;C = A^{\top}B^{\top}, \end{displaymath}$

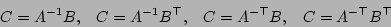
$\begin{displaymath}C = A^{-1}B,\;\;\;C = A^{-1}B^{\top},\;\;\;C = A^{-\top}B,\;\;\;C = A^{-\top}B^{\top} \end{displaymath}$

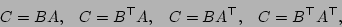
$\begin{displaymath}C = B A,\;\;\;C = B^{\top}A,\;\;\;C = B A^{\top},\;\;\;C = B^{\top}A^{\top}, \end{displaymath}$

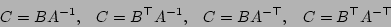
$\begin{displaymath}C = B A^{-1},\;\;\;C = B^{\top}A^{-1},\;\;\;C = B A^{-\top},\;\;\;C = B^{\top}A^{-\top} \end{displaymath}$

These operations are implemented by the following Gandalf routines:

  Gan_SquMatrix smA; /* square matrix A */
  Gan_Matrix mB, mC; /* matrices B & C */

  /* ... create and fill matrices A, B, create matrix C ... */

  /* routines right-multipling A by B */
  gan_squmat_rmult_q ( &smA, &mB, &mC ); /* C = A*B, OR */
  gan_squmat_rmultT_q ( &smA, &mB, &mC ); /* C = A*B^T, OR */
  gan_squmatT_rmult_q ( &smA, &mB, &mC ); /* C = A^T*B, OR */
  gan_squmatT_rmultT_q ( &smA, &mB, &mC ); /* C = A^T*B^T, OR */
  gan_squmatI_rmult_q ( &smA, &mB, &mC ); /* C = A^-1*B, OR */
  gan_squmatI_rmultT_q ( &smA, &mB, &mC ); /* C = A^-1*B^T, OR */
  gan_squmatIT_rmult_q ( &smA, &mB, &mC ); /* C = A^-T*B, OR */
  gan_squmatIT_rmultT_q ( &smA, &mB, &mC ); /* C = A^-T*B^T */

  /* routines left-multipling A by B */
  gan_squmat_lmult_q ( &smA, &mB, &mC ); /* C = B*A, OR */
  gan_squmat_lmultT_q ( &smA, &mB, &mC ); /* C = B^T*A, OR */
  gan_squmatT_lmult_q ( &smA, &mB, &mC ); /* C = B*A^T, OR */
  gan_squmatT_lmultT_q ( &smA, &mB, &mC ); /* C = B^T*A^T, OR */
  gan_squmatI_lmult_q ( &smA, &mB, &mC ); /* C = B*A^-1, OR */
  gan_squmatI_lmultT_q ( &smA, &mB, &mC ); /* C = B^T*A^-1, OR */
  gan_squmatIT_lmult_q ( &smA, &mB, &mC ); /* C = B*A^-T, OR */
  gan_squmatIT_lmultT_q ( &smA, &mB, &mC ); /* C = B^T*A^-T */

These routines have the alternative form

  Gan_SquMatrix smA; /* square matrix A */
  Gan_Matrix mB, *pmC; /* matrices B & C */

  /* ... create and fill matrices A, B ... */

  /* routines right-multipling A by B */
  pmC = gan_squmat_rmult_s ( &smA, &mB ); /* C = A*B, OR */
  pmC = gan_squmat_rmultT_s ( &smA, &mB ); /* C = A*B^T, OR */
  pmC = gan_squmatT_rmult_s ( &smA, &mB ); /* C = A^T*B, OR */
  pmC = gan_squmatT_rmultT_s ( &smA, &mB ); /* C = A^T*B^T, OR */
  pmC = gan_squmatI_rmult_s ( &smA, &mB ); /* C = A^-1*B, OR */
  pmC = gan_squmatI_rmultT_s ( &smA, &mB ); /* C = A^-1*B^T, OR */
  pmC = gan_squmatIT_rmult_s ( &smA, &mB ); /* C = A^-T*B, OR */
  pmC = gan_squmatIT_rmultT_s ( &smA, &mB ); /* C = A^-T*B^T */

  /* routines left-multipling A by B */
  pmC = gan_squmat_lmult_s ( &smA, &mB ); /* C = B*A, OR */
  pmC = gan_squmat_lmultT_s ( &smA, &mB ); /* C = B^T*A, OR */
  pmC = gan_squmatT_lmult_s ( &smA, &mB ); /* C = B*A^T, OR */
  pmC = gan_squmatT_lmultT_s ( &smA, &mB ); /* C = B^T*A^T, OR */
  pmC = gan_squmatI_lmult_s ( &smA, &mB ); /* C = B*A^-1, OR */
  pmC = gan_squmatI_lmultT_s ( &smA, &mB ); /* C = B^T*A^-1, OR */
  pmC = gan_squmatIT_lmult_s ( &smA, &mB ); /* C = B*A^-T, OR */
  pmC = gan_squmatIT_lmultT_s ( &smA, &mB ); /* C = B^T*A^-T */

The in-place versions will overwrite the contents of matrix 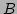$B$ with the result, and work fine unless 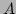$A$ is of symmetric type (in which case the error handler is invoked and NULL returned):

  Gan_SquMatrix smA; /* square matrix A */
  Gan_Matrix mB; /* matrix B */

  /* ... create and fill matrices A, B ... */

  /* routines right-multipling A by B */
  gan_squmat_rmult_i ( &smA, &mB ); /* replace B = A*B, OR */
  gan_squmat_rmultT_i ( &smA, &mB ); /* replace B = A*B^T, OR */
  gan_squmatT_rmult_i ( &smA, &mB ); /* replace B = A^T*B, OR */
  gan_squmatT_rmultT_i ( &smA, &mB ); /* replace B = A^T*B^T, OR */
  gan_squmatI_rmult_i ( &smA, &mB ); /* replace B = A^-1*B, OR */
  gan_squmatI_rmultT_i ( &smA, &mB ); /* replace B = A^-1*B^T, OR */
  gan_squmatIT_rmult_i ( &smA, &mB ); /* replace B = A^-T*B, OR */
  gan_squmatIT_rmultT_i ( &smA, &mB ); /* replace B = A^-T*B^T */

  /* routines left-multipling A by B */
  gan_squmat_lmult_i ( &smA, &mB ); /* replace B = B*A, OR */
  gan_squmat_lmultT_i ( &smA, &mB ); /* replace B = B^T*A, OR */
  gan_squmatT_lmult_i ( &smA, &mB ); /* replace B = B*A^T, OR */
  gan_squmatT_lmultT_i ( &smA, &mB ); /* replace B = B^T*A^T, OR */
  gan_squmatI_lmult_i ( &smA, &mB ); /* replace B = B*A^-1, OR */
  gan_squmatI_lmultT_i ( &smA, &mB ); /* replace B = B^T*A^-1, OR */
  gan_squmatIT_lmult_i ( &smA, &mB ); /* replace B = B*A^-T, OR */
  gan_squmatIT_lmultT_i ( &smA, &mB ); /* replace B = B^T*A^-T */

Now we consider multiplying a square matrix 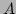$A$ by its own transpose, producing a symmetric matrix 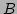$B$ . This operation will most often be applied to triangular matrices, and in Gandalf implicit transpose and inverse of the input matrix are supported, giving rise to the operations

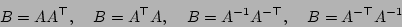
$\begin{displaymath}B = A A^{\top},\;\;\;\;B = A^{\top}A,\;\;\;\;B = A^{-1}A^{-\top},\;\;\;\;B = A^{-\top}A^{-1} \end{displaymath}$

which are implemented by the routines

  Gan_SquMatrix smA, smB; /* declare matrices A & B */

  /* ... create & fill matrix A, create (& optionally fill) matrix B ... */
  gan_squmat_srmultT_squ_q ( &smA, &smB ); /* set B = A*A^T, OR */
  gan_squmatT_srmult_squ_q ( &smA, &smB ); /* set B = A^T*A, OR */
  gan_squmatI_srmultIT_squ_q ( &smA, &smB ); /* set B = A^-1*A^-T, OR */
  gan_squmatIT_srmultI_squ_q ( &smA, &smB ); /* set B = A^-T*A^-1 */

There are also routines to build the result matrix 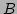$B$ from scratch:

  Gan_SquMatrix smA, *psmB; /* declare matrices A & B */

  /* ... create & fill matrix A ... */
  psmB = gan_squmat_srmultT_squ_s ( &smA ); /* create B = A*A^T, OR */
  psmB = gan_squmatT_srmult_squ_s ( &smA ); /* create B = A^T*A, OR */
  psmB = gan_squmatI_srmultIT_squ_s ( &smA ); /* create B = A^-1*A^-T, OR */
  psmB = gan_squmatIT_srmultI_squ_s ( &smA ); /* create B = A^-T*A^-1 */

and in-place versions of these operations are also available:

  Gan_SquMatrix smA; /* declare matrix A */

  /* ... create & fill matrix A ... */
  gan_squmat_srmultT_squ_i ( &smA ); /* replace A = A*A^T, OR */
  gan_squmatT_srmult_squ_i ( &smA ); /* replace A = A^T*A, OR */
  gan_squmatI_srmultIT_squ_i ( &smA ); /* replace A = A^-1*A^-T, OR */
  gan_squmatIT_srmultI_squ_i ( &smA ); /* replace A = A^-T*A^-1 */

Finally, there is a set of routines that multiply a symmetric matrix on left and right by a rectangular matrix and its transpose, producing another symmetric matrix. The operations implemented are

$\begin{displaymath}S' = A S A^{\top},\;\;\;\;\;\;S' = A^{\top}S A. \end{displaymath}$

This triple product is implemented as two matrix multiplications, and the matrix to hold the intermediate result is also passed in to the routines, so that it is also available on output. The routines are

  Gan_SquMatrix smS, smSp; /* declare matrices S & S' */
  Gan_Matrix mA, mB; /* declare matrices A & B */

  /* ... create & fill matrices S & A, create (& optionally fill) matrices B & Sp ... */
  gan_symmat_lrmult_q ( &smS, &mA, &mB, &smSp ); /* set B = S*A^T and Sp = A*S*A^T, OR */
  gan_symmat_lrmultT_q ( &smS, &mA, &mB, &smSp ); /* set B = S*A and Sp = A^T*S*A */

with alternative versions that create the result matrix 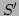$S'$ from scratch:

  Gan_SquMatrix smS, *psmSp; /* declare matrices S & S' */
  Gan_Matrix mA, mB; /* declare matrices A & B */

  /* ... create & fill matrices S & A, create (& optionally fill) matrix B ... */
  psmSp = gan_symmat_lrmult_s ( &smS, &mA, &mB ); /* set B = S*A^T and Sp = A*S*A^T, OR */
  psmSp = gan_symmat_lrmultT_s ( &smS, &mA, &mB ); /* set B = S*A and Sp = A^T*S*A */

It is allowable to pass NULL for the 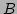$B$ matrix (&mB in the above function calls). In that case the intermediate result is computed and thrown away.

Next: Inverting a general size Up: General size matrices Previous: General size matrix/vector multiplication Contents

2006-03-17