Cholesky factorising a general size symmetric matrix (original) (raw)

Next: Symmetric matrix eigendecomposition Up: General size matrices Previous: Inverting a general size Contents

Cholesky factorising a general size symmetric matrix

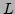The Cholesky factor of a symmetric positive definite matrix $S$ is a lower triangular matrix $L$ such that

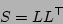
$\begin{displaymath}S = L L^{\top} \end{displaymath}$

and we write 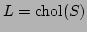$L={\rm chol}(S)$ . The Gandalf Cholesky factorisation routines apply to all symmetric types of matrix, i.e. GAN_SYMMETRIC_MATRIX itself,GAN_DIAGONAL_MATRIX and GAN_SCALED_IDENT_MATRIX. Routines are available to compute the factorisation, with the usual options, as follows:

  Gan_SquMatrix smS, smL, *psmL; /* declare matrices S & L */

  /* ... create and fill matrix S, which must be symmetric and positive definite,
         create L ... */
  gan_symmat_cholesky_q ( &smS, &smL ); /* L = chol(S), OR */
  psmL = gan_symmat_cholesky_s ( &smS ); /* L = chol(S) */
  gan_symmat_cholesky_i ( &smS ); /* replace S = chol(S) */

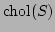The last option gan_symmat_cholesky_i() replaces $S$ in-place by ${\rm chol}(S)$ .

Error detection: If $S$ is not either symmetric or positive definite in the above routines, NULL is returned and the Gandalf error handler is invoked. Another failure mode is failing to create the result matrix.

2006-03-17