dsp.FilterCascade - Create cascade of filter System objects - MATLAB (original) (raw)

Create cascade of filter System objects

Description

The dsp.FilterCascade object creates a multistage System object™ that enables cascading of filter System objects and scalar gains. This object operates similar to the cascade function. However, thecascade function does not support delay as a filter stage.

You can pass the dsp.FilterCascade System object as a stage to another dsp.FilterCascade System object. You can also pass dsp.FilterCascade System object as an input to the cascade function.

When you call the object, the size, data type, and complexity of the input signal must be supported by all of the stages in the filter cascade. This object supports variable-size signals if the filter stages within the object support variable-size signals.

To filter a signal with a cascade of filters:

Create the dsp.FilterCascade object and set its properties.
Call the object with arguments, as if it were a function.

To learn more about how System objects work, see What Are System Objects?

Alternatively, you can generate a MATLAB® function from the filter cascade object, and call that function to filter a signal. The generated function supports C/C++ code generation. For more details, see thegenerateFilteringCode function.

Creation

Syntax

Description

`FC` = dsp.FilterCascade returns a System object, FC that has a single stage, a dsp.FIRFilter System object with default properties.

`FC` = dsp.FilterCascade(filt1,filt2,...,filtn) returns a multistage System object, FC, with the first stage set tofilt1, the second stage set to filt2, and so on. Each stage can be a filter System object or a scalar gain value.

For example, create a filter cascade that includes a lowpass filter, a highpass filter, and a gain stage.

lpFilt = dsp.LowpassFilter(StopbandFrequency=15000,... PassbandFrequency=12000); hpFilt = dsp.HighpassFilter(StopbandFrequency=5000,... PassbandFrequency=8000); gain = 2; bpFilt = dsp.FilterCascade(lpFilt,hpFilt,2);

example

Properties

expand all

Unless otherwise indicated, properties are nontunable, which means you cannot change their values after calling the object. Objects lock when you call them, and therelease function unlocks them.

If a property is tunable, you can change its value at any time.

For more information on changing property values, seeSystem Design in MATLAB Using System Objects.

Filter stage, specified as a filter System object or a scalar gain value. To see which System objects you can add to a filter cascade, use:

dsp.FilterCascade.helpSupportedSystemObjects

You can modify an existing stage by modifying the associated property. For example:

FC = dsp.FilterCascade(dsp.FIRFilter,5)

FC =

dsp.FilterCascade with properties:

Stage1: [1×1 dsp.FIRFilter]
Stage2: 5

K>> FC.Stage2 = dsp.FIRDecimator

FC =

dsp.FilterCascade with properties:

Stage1: [1×1 dsp.FIRFilter]
Stage2: [1×1 dsp.FIRDecimator]

To change the number of stages in a cascade, use the addStage and removeStage functions.

Usage

Syntax

Description

[y](#mw%5F05be6689-f3f6-4e41-bd28-47e8d8a897e9) = FC([x](#mw%5F99289b13-d35b-4ca2-8815-b584754c611f)) filters input signal x by using the filter cascade defined inFC and returns filtered output y. The size, data type, and complexity of the input signal must be supported by all of the stages in the filter cascade. This object supports variable-size signals if the filter stages within the object support variable-size signals.

example

Input Arguments

expand all

Data input, specified as a vector or a matrix. When the input is a matrix, each column of the matrix represents an independent data channel.

Data Types: single | double
Complex Number Support: Yes

Output Arguments

expand all

Filtered output data, returned as a vector or a matrix. The size, data type, and complexity of the output signal matches that of the input signal.

Data Types: double | single
Complex Number Support: Yes

Object Functions

To use an object function, specify the System object as the first input argument. For example, to release system resources of a System object named obj, use this syntax:

expand all

step	Run System object algorithm
release	Release resources and allow changes to System object property values and input characteristics
reset	Reset internal states of System object

Examples

collapse all

Design a bandpass filter by cascading:

A highpass filter with a stopband frequency of 5000 Hz and a passband frequency of 8000 Hz
A lowpass filter with a passband frequency of 12,000 Hz and a stopband frequency of 15,000 Hz

Visualize the frequency response.

lpFilt = dsp.LowpassFilter(StopbandFrequency=15000,... PassbandFrequency=12000); hpFilt = dsp.HighpassFilter(StopbandFrequency=5000,... PassbandFrequency=8000);

bpFilt = dsp.FilterCascade(lpFilt,hpFilt);

filterAnalyzer(bpFilt,FilterNames="BandpassFilter");

Pass a noisy sine wave as the input to the bandpass filter. The input is a sum of three sine waves with frequencies at 3 kHz, 10 kHz, and 15 kHz. The sampling frequency is 48 kHz. View the input and the filtered output on a spectrum analyzer.

The tones at 3 kHz and 15 kHz are attenuated, and the tone at 10 kHz is preserved by the bandpass filter.

Sine1 = dsp.SineWave(Frequency=3e3,... SampleRate=48e3,... SamplesPerFrame=6000); Sine2 = dsp.SineWave(Frequency=10e3,... SampleRate=48e3,... SamplesPerFrame=6000); Sine3 = dsp.SineWave(Frequency=15e3,... SampleRate=48e3,... SamplesPerFrame=6000);

SpecAna = spectrumAnalyzer(... PlotAsTwoSidedSpectrum=false,... SampleRate=Sine1.SampleRate, ... ShowLegend=true, ... YLimits=[-160,60]);

SpecAna.ChannelNames = {"Original noisy signal","Filtered signal"};

for i = 1:1000 x = Sine1()+Sine2()+Sine3()+0.1.*randn(Sine1.SamplesPerFrame,1); y = bpFilt(x); SpecAna(x,y);

end release(SpecAna)

Create a CIC decimator. Cascade the decimator with a gain.

cicdecim = dsp.CICDecimator(... DecimationFactor=6,... NumSections=6); decimcasc = dsp.FilterCascade(cicdecim,... 1/gain(cicdecim));

Design a compensation decimator and cascade it with the filter cascade, decimcasc. This operation nests a dsp.FilterCascade object as a stage in another filter cascade. The CIC compensation decimator has an inherent gain, gain(cicdecim). The factor of 1/gain(cicdecim) from the decimation filter cascade, decimcasc, compensates for the compensation filter gain.

% Sample rate of input of compensation decimator fs = 16e3;
% Passband frequency fPass = 4e3;
% Stopband frequency fStop = 4.5e3; ciccomp = dsp.CICCompensationDecimator(cicdecim,... DecimationFactor=2, ... PassbandFrequency=fPass, ... StopbandFrequency=fStop, ... SampleRate=fs); filtchain = dsp.FilterCascade(decimcasc,ciccomp);

Visualize the frequency response of the cascade of cascades.

f = filterAnalyzer(decimcasc,ciccomp,... filtchain,SampleRates=[fs6,fs,fs6],... Arithmetic="fixed"); showFilters(f,false,... FilterNames=["decimcasc_Stage1","decimcasc_Stage2","filtchain_Stage1",... "filtchain_Stage1_Stage1","filtchain_Stage1_Stage2","filtchain_Stage2"]) setLegendStrings(f,["CIC Decimator",... "CIC Compensation Decimator",... "Overall Response"]);

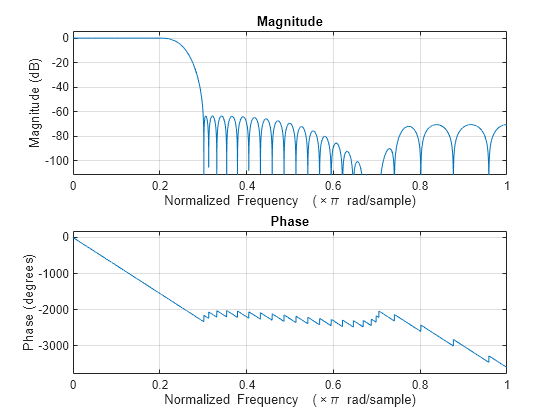
Design a two-stage decimator with a 100-Hz transition width, a 2-kHz sampling frequency, and 60-dB attenuation in the stopband. The decimator needs to downsample by a factor of 4.

filtCasc = designRateConverter(DecimationFactor=4,... InputSampleRate=2000,Bandwidth=200,StopbandAttenuation=60,... Verbose=true)

designRateConverter(InterpolationFactor=1, DecimationFactor=4, InputSampleRate=2000, Bandwidth=200, StopbandAttenuation=60, MaxStages=Inf, CostMethod="estimate", OptimizeFor="MPIS", Tolerance=0, ToleranceUnits="absolute")

Conversion ratio: 1:4 Input sample rate: 2000 Output sample rate: 500

filtCasc = dsp.FilterCascade with properties:

     Stage1: [1×1 dsp.FIRDecimator]
     Stage2: [1×1 dsp.FIRDecimator]
CloneStages: true

Verify your design.

ans = 'Discrete-Time Filter Cascade ---------------------------- Number of stages: 2 Stage cloning: enabled

 Stage1: dsp.FIRDecimator
 -------
 Discrete-Time FIR Multirate Filter (real)               
 -----------------------------------------               
 Filter Structure   : Direct-Form FIR Polyphase Decimator
 Decimation Factor  : 2                                  
 Polyphase Length   : 10                                 
 Filter Length      : 19                                 
 Stable             : Yes                                
 Linear Phase       : Yes (Type 1)                       
                                                         
 Arithmetic         : double                             
 
 
 Stage2: dsp.FIRDecimator
 -------
 Discrete-Time FIR Multirate Filter (real)               
 -----------------------------------------               
 Filter Structure   : Direct-Form FIR Polyphase Decimator
 Decimation Factor  : 2                                  
 Polyphase Length   : 18                                 
 Filter Length      : 35                                 
 Stable             : Yes                                
 Linear Phase       : Yes (Type 1)                       
                                                         
 Arithmetic         : double                             
 
 '

$Figure contains 2 axes objects. Axes object 1 with title Phase, xlabel Normalized Frequency (\times\pi rad/sample), ylabel Phase (degrees) contains an object of type line. Axes object 2 with title Magnitude, xlabel Normalized Frequency (\times\pi rad/sample), ylabel Magnitude (dB) contains an object of type line.$

Generate code to filter data using this design. You cannot generate C/C++ code from the dsp.FilterCascade object directly, but you can generate C/C++ code from the generated function. The function defines the filter stages and calls them in sequence. The function is saved in a file called myDecimator.m in the current directory.

generateFilteringCode(filtCasc,"myDecimator");

The myDecimator function creates a filter cascade and calls each stage object in turn.

function y = myDecimator(x) %MYDECIMATOR Construct a filter cascade and process its stages

% MATLAB Code % Generated by MATLAB(R) 25.1 and DSP System Toolbox 25.1. % Generated on: 02-Feb-2025 16:43:14

% To generate C/C++ code from this function use the codegen command. % Type 'help codegen' for more information. %#codegen

%% Construction persistent firdn1 firdn2 if isempty(firdn1) firdn1 = dsp.FIRDecimator( ... Numerator=[0.0021878514650437845 0 -0.010189095418136306 0 0.031140395225498115 0 -0.082785931644222821 0 0.30979571849010851 0.5 0.30979571849010851 0 -0.082785931644222821 0 0.031140395225498115 0 -0.010189095418136306 0 0.0021878514650437845]); firdn2 = dsp.FIRDecimator( ... Numerator=[0.0011555011750488237 0 -0.0027482166351233102 0 0.0057681982289523072 0 -0.010736374060960912 0 0.018592020073668478 0 -0.031093723586671229 0 0.052603914610235683 0 -0.099130756073130377 0 0.31592697826202448 0.5 0.31592697826202448 0 -0.099130756073130377 0 0.052603914610235683 0 -0.031093723586671229 0 0.018592020073668478 0 -0.010736374060960912 0 0.0057681982289523072 0 -0.0027482166351233102 0 0.0011555011750488237]); end

%% Process y1 = firdn1(x); y = firdn2(y1);

Extended Capabilities

expand all

Usage notes and limitations:

You cannot generate code directly from dsp.FilterCascade. If the filters in each stage support code generation, you can generate C/C++ code from the function returned bygenerateFilteringCode.
See System Objects in MATLAB Code Generation (MATLAB Coder).

Version History

Introduced in R2014b

expand all

Starting in R2025a, the Filter Design HDL Coder™ product is discontinued. So, this object no longer supports HDL code generation by using the generatehdl function. For modeling a chain of filters for HDL code generation, see the Implement Digital Downconverter for FPGA (DSP HDL Toolbox) and Implement Digital Upconverter for FPGA (DSP HDL Toolbox) examples. These examples show a Simulink® implementation. You can model the same algorithm in MATLAB by using DSP HDL Toolbox™ System objects.