Optimizing Nonlinear Functions - MATLAB & Simulink (original) (raw)

Minimizing Functions of One Variable

Given a mathematical function of a single variable, you can use the fminbnd function to find a local minimizer of the function in a given interval. For example, consider the humps.m function, which is provided with MATLAB®. The following figure shows the graph of humps.

x = -1:.01:2; y = humps(x); plot(x,y) xlabel('x') ylabel('humps(x)') grid on

Figure contains an axes object. The axes object with xlabel x, ylabel humps(x) contains an object of type line.

To find the minimum of the humps function in the range (0.3,1), use

x = fminbnd(@humps,0.3,1)

You can see details of the solution process by using optimset to create options with the Display option set to 'iter'. Pass the resulting options to fminbnd.

options = optimset('Display','iter'); x = fminbnd(@humps,0.3,1,options)

Func-count x f(x) Procedure 1 0.567376 12.9098 initial 2 0.732624 13.7746 golden 3 0.465248 25.1714 golden 4 0.644416 11.2693 parabolic 5 0.6413 11.2583 parabolic 6 0.637618 11.2529 parabolic 7 0.636985 11.2528 parabolic 8 0.637019 11.2528 parabolic 9 0.637052 11.2528 parabolic

Optimization terminated: the current x satisfies the termination criteria using OPTIONS.TolX of 1.000000e-04

The iterative display shows the current value of x and the function value at f(x) each time a function evaluation occurs. For fminbnd, one function evaluation corresponds to one iteration of the algorithm. The last column shows the procedure fminbnd uses at each iteration, a golden section search or a parabolic interpolation. For details, see Optimization Solver Iterative Display.

Note: Optimization solvers apply to real-valued functions. Complex values cannot be optimized, except for a real-valued function of the complex values, such as the norm.

Minimizing Functions of Several Variables

The fminsearch function is similar to fminbnd except that it handles functions of many variables. Specify a starting vector _x_0 rather than a starting interval. fminsearch attempts to return a vector x that is a local minimizer of the mathematical function near this starting vector.

To try fminsearch, create a function three_var of three variables, x, y, and z.

function b = three_var(v) x = v(1); y = v(2); z = v(3); b = x.^2 + 2.5sin(y) - z^2x^2*y^2;

Now find a minimum for this function using x = -0.6, y = -1.2, and z = 0.135 as the starting values.

v = [-0.6,-1.2,0.135]; a = fminsearch(@three_var,v)

a = 0.0000 -1.5708 0.1803

Note

Optimization solvers apply to real-valued functions. Complex values cannot be optimized, except for a real-valued function of the complex values, such as the norm.

Maximizing Functions

The fminbnd and fminsearch solvers attempt to minimize an objective function. If you have a maximization problem, that is, a problem of the form

then define g(x) = –f(x), and minimize g.

For example, to find the maximum of tan(cos(x)) near x = 5, evaluate:

[x fval] = fminbnd(@(x)-tan(cos(x)),3,8)

x = 6.2832

fval = -1.5574

The maximum is 1.5574 (the negative of the reported fval), and occurs at x = 6.2832. This answer is correct since, to five digits, the maximum is tan(1) = 1.5574, which occurs at x = 2_π_ = 6.2832.

fminsearch Algorithm

fminsearch uses the Nelder-Mead simplex algorithm as described in Lagarias et al. [1]. This algorithm uses a simplex of n + 1 points for _n_-dimensional vectors x. The algorithm first makes a simplex around the initial guess _x_0 by adding 5% of each component _x_0(i) to _x_0. The algorithm uses these n vectors as elements of the simplex in addition to _x_0. (The algorithm uses 0.00025 as component i if _x_0(i) = 0.) Then, the algorithm modifies the simplex repeatedly according to the following procedure.

Note

The keywords for the fminsearch iterative display appear in bold after the description of the step.

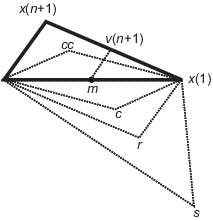
  1. Let x(i) denote the list of points in the current simplex,i = 1,...,n + 1.
  2. Order the points in the simplex from lowest function value_f_(x(1)) to highest_f_(x(n + 1)). At each step in the iteration, the algorithm discards the current worst point_x_(n + 1), and accepts another point into the simplex. [Or, in the case of step 7 below, it changes all_n_ points with values above_f_(x(1))].
  3. Generate the reflected point
    where
    m = Σ_x_(i)/n,i = 1...n, (2)
    and calculate f(r).
  4. If f(x(1)) ≤f(r) <f(x(n)), accept_r_ and terminate this iteration. Reflect
  5. If f(r) <f(x(1)), calculate the expansion point s
    s = m + 2(m – x(n + 1)), (3)
    and calculate f(s).
    1. If f(s) <f(r), accept_s_ and terminate the iteration. Expand
    2. Otherwise, accept r and terminate the iteration. Reflect
  6. If f(r) ≥f(x(n)), perform a contraction between m and either_x_(n + 1) or_r_, depending on which has the lower objective function value.
    1. If f(r) <f(x(n + 1)) (that is, r is better than_x_(n + 1)), calculate
      and calculate f(c). If f(c) < f(r), accept c and terminate the iteration. Contract outside
      Otherwise, continue with Step 7 (Shrink).
    2. If f(r) ≥f(x(n + 1)), calculate
      cc = m + (x(n + 1) –m)/2 (5)
      and calculate f(cc). If f(cc) < f(x(n + 1)), accept cc and terminate the iteration. Contract inside
      Otherwise, continue with Step 7 (Shrink).
  7. Calculate the n points
    v(i) =x(1) + (x(i) –x(1))/2 (6)
    and calculate_f_(v(i)),i = 2,...,n + 1. The simplex at the next iteration is x(1),v(2),...,v(n + 1). Shrink

The following figure shows the points that fminsearch can calculate in the procedure, along with each possible new simplex. The original simplex has a bold outline. The iterations proceed until they meet a stopping criterion.

Graphical representation of fminsearch algorithm showing reflection, expansion, contraction, and shrinking points.

Reference

[1] Lagarias, J. C., J. A. Reeds, M. H. Wright, and P. E. Wright. “Convergence Properties of the Nelder-Mead Simplex Method in Low Dimensions.” SIAM Journal of Optimization, Vol. 9, Number 1, 1998, pp. 112–147.

See Also

Topics