median - Median value of array - MATLAB (original) (raw)
Syntax
Description
M = median([A](#btrh56u-1-A)) returns the median value of A.
- If
Ais a vector, thenmedian(A)returns the median value ofA. - If
Ais a nonempty matrix, thenmedian(A)treats the columns ofAas vectors and returns a row vector of median values. - If
Ais an empty 0-by-0 matrix,median(A)returnsNaN. - If
Ais a multidimensional array, thenmedian(A)treats the values along the first array dimension whose size does not equal 1 as vectors. The size ofMin this dimension becomes1, while the sizes of all other dimensions remain the same as inA. - If
Ais a table or timetable, thenmedian(A)returns a one-row table containing the median of each variable. (since R2023a)
median returns natively in the class of A, such thatclass(M) = class(A).
M = median([A](#btrh56u-1-A),`"all"`) returns the median over all elements of A.
M = median([A](#btrh56u-1-A),[dim](#btrh56u-1-dim)) returns the median of elements along dimension dim. For example, ifA is a matrix, then median(A,2) returns a column vector containing the median value of each row.
M = median([A](#btrh56u-1-A),[vecdim](#mw%5Fe28cd7fe-a88d-43b3-92e3-cd2ae92b1428)) returns the median based on the dimensions specified in the vectorvecdim. For example, if A is a matrix, then median(A,[1 2]) returns the median of all elements inA because every element of a matrix is contained in the array slice defined by dimensions 1 and 2.
M = median(___,[missingflag](#mw%5F205279be-261a-485f-b59a-e3715d4699c3)) specifies whether to include or omit missing values in A for any of the previous syntaxes. For example, median(A,"omitmissing") ignores all missing values when computing the median. By default,median includes missing values.
M = median(___,Weights=[W](#mw%5Fb39e7c84-51b1-47c1-8a6d-840d9f921e33)) specifies a weighting scheme W and returns the weighted median. (since R2024a)
Examples
Define a 4-by-3 matrix.
A = [0 1 1; 2 3 2; 1 3 2; 4 2 2]
A = 4×3
0 1 1
2 3 2
1 3 2
4 2 2Find the median value of each column.
M = 1×3
1.5000 2.5000 2.0000For each column, the median value is the mean of the middle two numbers in sorted order.
Define a 2-by-3 matrix.
Find the median value of each row.
For each row, the median value is the middle number in sorted order.
Create a 1-by-3-by-4 array of integers between 1 and 10.
rng('default') A = randi(10,[1,3,4])
A = A(:,:,1) =
9 10 2A(:,:,2) =
10 7 1A(:,:,3) =
3 6 10A(:,:,4) =
10 2 10Find the median values of this 3-D array along the second dimension.
M = M(:,:,1) =
9M(:,:,2) =
7M(:,:,3) =
6M(:,:,4) =
10This operation produces a 1-by-1-by-4 array by computing the median of the three values along the second dimension. The size of the second dimension is reduced to 1.
Compute the median along the first dimension of A.
M = median(A,1); isequal(A,M)
This command returns the same array as A because the size of the first dimension is 1.
Create a 3-D array and compute the median over each page of data (rows and columns).
A(:,:,1) = [2 4; -2 1]; A(:,:,2) = [6 2; -5 3]; A(:,:,3) = [4 4; 7 -3]; M1 = median(A,[1 2])
M1 = M1(:,:,1) =
1.5000M1(:,:,2) =
2.5000M1(:,:,3) =
4To compute the median over all dimensions of an array, you can either specify each dimension in the vector dimension argument, or use the "all" option.
Define a 1-by-4 vector of 8-bit integers.
A = 1×4 int8 row vector
1 2 3 4
Compute the median value.
M is the mean of the middle two numbers in sorted order returned as an 8-bit integer.
Create a matrix containing NaN values.
A = [1.77 -0.005 NaN -2.95; NaN 0.34 NaN 0.19]
A = 2×4
1.7700 -0.0050 NaN -2.9500
NaN 0.3400 NaN 0.1900Compute the median values of the matrix, excluding missing values. For matrix columns that contain any NaN value, the median is computed over non-NaN elements. For matrix columns that contain all NaN values, the median is NaN.
M = median(A,"omitmissing")
M = 1×4
1.7700 0.1675 NaN -1.3800Since R2024a
Create a matrix and compute the weighted median of the matrix according to a weighting scheme specified by W. The median function applies the weighting scheme to each column in A.
A = [1 1; 7 9; 1 9; 1 9; 6 2]; W = [1 2 1 2 3]'; M = median(A,Weights=W)
For each column, the median value is the mean of the middle two numbers in sorted order.
Input Arguments
Input data, specified as a vector, matrix, multidimensional array, table, or timetable.
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | logical | categorical | datetime | duration | table | timetable
Dimension to operate along, specified as a positive integer scalar. If you do not specify the dimension, then the default is the first array dimension whose size does not equal 1.
Dimension dim indicates the dimension whose length reduces to 1. The size(M,dim) is 1, while the sizes of all other dimensions remain the same.
Consider an m-by-n input matrix,A:
median(A,1)computes the median of the elements in each column ofAand returns a1-by-nrow vector.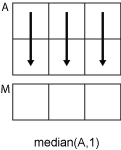
median(A,2)computes the median of the elements in each row ofAand returns anm-by-1column vector.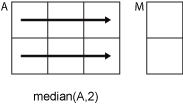
median returns A when dim is greater than ndims(A).
Vector of dimensions, specified as a vector of positive integers. Each element represents a dimension of the input array. The lengths of the output in the specified operating dimensions are 1, while the others remain the same.
Consider a 2-by-3-by-3 input array, A. Thenmedian(A,[1 2]) returns a 1-by-1-by-3 array whose elements are the medians of each page of A.

Missing value condition, specified as one of the values in this table.
| Value | Input Data Type | Description |
|---|---|---|
| "includemissing" | All supported data types | Include missing values inA when computing the median. If any element in the operating dimension is missing, then the corresponding element in M is missing. |
| "includenan" | double, single,duration | |
| "includenat" | datetime | |
| "includeundefined" | categorical | |
| "omitmissing" | All supported data types | Ignore missing values inA, and compute the median over fewer points. If all elements in the operating dimension are missing, then the corresponding element inM is missing. |
| "omitnan" | double, single,duration | |
| "omitnat" | datetime | |
| "omitundefined" | categorical |
Since R2024a
Weighting scheme, specified as a vector, matrix, or multidimensional array. The elements of W must be nonnegative.
If you specify a weighting scheme, median returns the weighted median, which is the value in A associated with a cumulative 50% of the weights specified by W [1]. The weighted median is less affected by extreme values compared to the standard median.
If W is a vector, it must have the same length as the operating dimension. Otherwise, W must have the same size as the input data.
If the input data A is a table or timetable, thenW must be a vector.
You cannot specify this argument if you specify vecdim or "all".
Data Types: double | single
Algorithms
For ordinal categorical arrays, MATLAB® interprets the median of an even number of elements as follows:
| If the number of categories between the middle two values is ... | Then the median is ... |
|---|---|
| zero (values are from consecutive categories) | larger of the two middle values |
| an odd number | value from category occurring midway between the two middle values |
| an even number | value from larger of the two categories occurring midway between the two middle values |
References
Extended Capabilities
Themedian function supports tall arrays with the following usage notes and limitations:
- Input
Amust be a column vector to computemedianin the first dimension. - The
Weightsname-value argument is not supported.
For more information, see Tall Arrays.
Usage notes and limitations:
- If used, the
dimandvecdimarguments must be constant at code generation time. - For input argument
A:- If you do not specify a dimension, the code generator operates along the first dimension of the input array that is variable size or whose size does not equal 1. If this dimension is variable size at code generation time and is 1 at run time, a run-time error can occur. To avoid this error, specify the dimension.
- If all dimensions of the input array are variable size at code generation time, this array cannot be empty at run time.
- In the generated code, the input array remains complex, even if all of its elements have zero-valued imaginary parts. Under these circumstances, the results produced by the generated code might differ from those produced by MATLAB. See Code Generation for Complex Data with Zero-Valued Imaginary Parts (MATLAB Coder).
Usage notes and limitations:
Refer to the usage notes and limitations in the C/C++ Code Generation section. The same limitations apply to GPU code generation.
The median function fully supports GPU arrays. To run the function on a GPU, specify the input data as a gpuArray (Parallel Computing Toolbox). For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).
Version History
Introduced before R2006a
GPU Coder™ now generates more optimized CUDA® code for median. You must haveMATLAB Coder™ and GPU Coder to generate CUDA code.
You can compute the weighted median for input data having thedatetime and ordinal categorical data types. Before R2024b, you could compute only the unweighted median for these data types.
The median function has improved performance when you specify a weighting scheme.
For example, this code computes the weighted median of a 600-by-10 matrix. The code is about 1.8x faster than in the previous release.
function timingTest A = rand(600,10); W = rand(600,1);
for i = 1:1:3e2 median(A,Weights=W); end end
The approximate execution times are:
R2024a: 1.00 s
R2024b: 0.55 s
The code was timed on a Windows® 11, AMD EPYC 74F3 24-Core Processor @ 3.19 GHz test system using thetimeit function.
Compute the weighted median by specifying the Weights parameter as the weighting scheme. You can compute the weighted median for input data having numeric, logical, and duration data types.
Include or omit all missing values in the input array when computing the median by using the "includemissing" or "omitmissing" options. Previously, "includenan", "omitnan","includenat", "omitnat","includeundefined", and "omitundefined" specified a missing value condition that was specific to the data type of the input array.
The median function can calculate on all variables within a table or timetable without indexing to access those variables. All variables must have data types that support the calculation. For more information, see Direct Calculations on Tables and Timetables.
Operate on multiple dimensions of the input array at a time. Specify a vector of operating dimensions, or specify the "all" option to operate on all array dimensions.