tan - Tangent of argument in radians - MATLAB (original) (raw)

Tangent of argument in radians

Syntax

Description

[Y](#bt5p42g-1-Y) = tan([X](#bt5p42g-1-X)) returns the tangent of each element of X. The tan function operates element-wise on arrays. The function accepts both real and complex inputs.

For real values of X, tan(X) returns real values in the interval [-∞, ∞].
For complex values of X,tan(X) returns complex values.

example

Examples

collapse all

Plot the tangent function over the domain -π/2≤x≤π/2.

x = (-pi/2)+0.01:0.01:(pi/2)-0.01; plot(x,tan(x)), grid on

Figure contains an axes object. The axes object contains an object of type line.

Calculate the tangent of the complex angles in vector x.

x = [-i pi+ipi/2 -1+i4]; y = tan(x)

y = 1×3 complex

0.0000 - 0.7616i -0.0000 + 0.9172i -0.0006 + 1.0003i

Input Arguments

collapse all

Input angle in radians, specified as a scalar, vector, matrix, multidimensional array, table, or timetable.

Data Types: single | double | table | timetable
Complex Number Support: Yes

Output Arguments

collapse all

Tangent of input angle, returned as a real-valued or complex-valued scalar, vector, matrix, multidimensional array, table, or timetable.

More About

collapse all

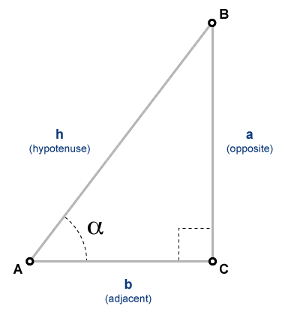
The tangent of an angle, α, defined with reference to a right triangle is

Right triangle with vertices A, B, and C. The vertex A has an angle α, and the vertex C has a right angle. The hypotenuse, or side AB, is labeled as h. The opposite side of α, or side BC, is labeled as a. The adjacent side of α, or side AC, is labeled as b. The tangent of α is defined as the opposite side a divided by the adjacent side b.

The tangent of a complex argument, α, is

Tips

In floating-point arithmetic, tan is a bounded function. That is, tan does not return values of Inf or-Inf at points of divergence that are multiples ofpi, but a large magnitude number instead. This stems from the inaccuracy of the floating-point representation of π.

Extended Capabilities

expand all

Thetan function fully supports tall arrays. For more information, see Tall Arrays.

The tan function fully supports GPU arrays. To run the function on a GPU, specify the input data as a gpuArray (Parallel Computing Toolbox). For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).

Version History

Introduced before R2006a

expand all

The tan function can calculate on all variables within a table or timetable without indexing to access those variables. All variables must have data types that support the calculation. For more information, see Direct Calculations on Tables and Timetables.