ilu - Incomplete LU factorization - MATLAB (original) (raw)

Incomplete LU factorization

Syntax

Description

[[L](#mw%5Faa0a5446-3e40-4986-af30-f061365c378f),[U](#mw%5F19b2c217-1da6-448a-940d-0a0c12ee7587)] = ilu([A](#mw%5Fb053ef4c-2b70-4832-adfe-b02c70ffeddd)) performs the incomplete LU factorization of a sparse matrix A with zero-fill, and returns the lower triangular matrix L and the upper triangular matrix U.

example

[[L](#mw%5Faa0a5446-3e40-4986-af30-f061365c378f),[U](#mw%5F19b2c217-1da6-448a-940d-0a0c12ee7587),[P](#mw%5F9318c26c-9146-4256-8b29-5d6988dbd2dc)] = ilu([A](#mw%5Fb053ef4c-2b70-4832-adfe-b02c70ffeddd)) also returns the permutation matrix P such that L and U are incomplete factors of P*A orA*P. By default, P is an identity matrix for the incomplete LU factorization without pivoting.

[W](#mw%5F5d261b66-3c7c-417b-91c7-65281935b934) = ilu([A](#mw%5Fb053ef4c-2b70-4832-adfe-b02c70ffeddd)) returns the nonzeros of the LU factors. The output W is equal to L + U - speye(size(A)).

example

[___] = ilu([A](#mw%5Fb053ef4c-2b70-4832-adfe-b02c70ffeddd),[options](#mw%5Fbe0d234f-6566-457b-b106-dbc6bf5e7d91)) performs the incomplete LU factorization of A with options specified by the structure options.

For example, you can perform an incomplete LU factorization with pivoting by setting the type field of options to"ilutp". You can then specify a row-sum or column-sum preserving modified incomplete LU factorization by setting the milu field to"row" or "col". This combination of options returns the permutation matrix P such that L andU are incomplete factors of A*P for the"row" option (where U is column permuted), orL and U are incomplete factors ofP*A for the "col" option (whereL is row permuted).

example

Examples

collapse all

The ilu function provides three types of incomplete LU factorizations: the zero-fill factorization (ILU(0)), the Crout version (ILUC), and the factorization with threshold dropping and pivoting (ILUTP).

By default, ilu performs the zero-fill incomplete LU factorization of a sparse matrix input. For example, find the complete and incomplete factorization of a sparse matrix with 7840 nonzeros. Its complete LU factors have 126,478 nonzeros, and its incomplete LU factors with zero-fill have 7840 nonzeros, the same number as A.

A = gallery("neumann",1600) + speye(1600); n = nnz(A)

Because the zero-fill factorization preserves the sparsity pattern of the input matrix in its LU factors, the relative error of the factorization is essentially zero on the pattern of nonzero elements of A.

[L,U] = ilu(A); e = norm(A-(L*U).*spones(A),"fro")/norm(A,"fro")

However, the product of these zero-fill factors is not a good approximation of the original matrix.

e = norm(A-L*U,"fro")/norm(A,"fro")

To improve the accuracy, you can use other types of incomplete LU factorization with fill-in. For example, use the Crout version with a 1e-6 drop tolerance.

options.droptol = 1e-6; options.type = "crout"; [L,U] = ilu(A,options);

The Crout version of the incomplete factorization has 51,482 nonzeros in its LU factors (less than the complete factorization). With fill-in, the product of the incomplete LU factors is a better approximation of the original matrix.

e = norm(A-L*U,"fro")./norm(A,"fro")

For comparison, for the same input matrix A, the incomplete factorization with threshold dropping and pivoting gives results similar to the Crout version.

options.type = "ilutp"; [L,U,P] = ilu(A,options); n = nnz(ilu(A,options))

norm(PA-LU,"fro")./norm(A,"fro")

Change the drop tolerance of incomplete LU factorization to factor a sparse matrix.

Load the west0479 matrix, which is a real-valued 479-by-479 nonsymmetric sparse matrix. Estimate the condition number of the matrix by using condest.

load west0479 A = west0479; c1 = condest(A)

Improve the condition number of the matrix by using equilibrate. Permute and rescale the original matrix A to create a new matrix B = R*P*A*C, which has a better condition number and diagonal entries of only 1 and –1.

[P,R,C] = equilibrate(A); B = RPA*C; c2 = condest(B)

Specify the options to perform the incomplete LU factorization of B with threshold dropping and pivoting that preserves the row sum. For comparison purposes, first specify a zero drop tolerance of fill-in, which produces the complete LU factorization.

options.type = "ilutp"; options.milu = "row"; options.droptol = 0; [L,U,P] = ilu(B,options);

This factorization is very accurate in approximating the input matrix B, but the factors are significantly more dense than B.

e = norm(BP-LU,"fro")/norm(B,"fro")

nLU = nnz(L)+nnz(U)-size(B,1)

You can change the drop tolerance to obtain incomplete LU factors that are more sparse but less accurate in approximating B. For example, the following plots show the ratio of the density of the incomplete factors to the density of the input matrix plotted against the drop tolerance, and the relative error of the incomplete factorization.

ntols = 20; tau = logspace(-6,-2,ntols); e = zeros(1,ntols); nLU = zeros(1,ntols); for k = 1:ntols options.droptol = tau(k); [L,U,P] = ilu(B,options); nLU(k) = nnz(L)+nnz(U)-size(B,1); e(k) = norm(BP-LU,"fro")/norm(B,"fro"); end figure semilogx(tau,nLU./nB,LineWidth=2) title("Ratio of nonzeros of LU factors with respect to B") xlabel("drop tolerance") ylabel("nnz(L)+nnz(U)-size(B,1)/nnz(B)",FontName="FixedWidth")

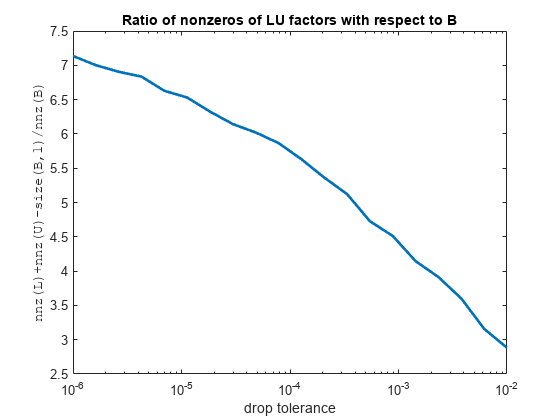
Figure contains an axes object. The axes object with title Ratio of nonzeros of LU factors with respect to B, xlabel drop tolerance, ylabel nnz(L)+nnz(U)-size(B,1)/nnz(B) contains an object of type line.

figure loglog(tau,e,LineWidth=2) title("Relative error of the incomplete LU factorization") xlabel("drop tolerance") ylabel("$||BP-LU||_F,/,||B||_F$",Interpreter="latex")

$Figure contains an axes object. The axes object with title Relative error of the incomplete LU factorization, xlabel drop tolerance, ylabel <math xmlns="http://www.w3.org/1998/Math/MathML"><semantics><mrow><mi mathvariant="normal">∣</mi><mi mathvariant="normal">∣</mi><mi>B</mi><mi>P</mi><mo>−</mo><mi>L</mi><mi>U</mi><mi mathvariant="normal">∣</mi><mi mathvariant="normal">∣</mi><mi>i</mi><mi>n</mi><mi>d</mi><mi>e</mi><mi>x</mi><mi>O</mi><mi>f</mi><mi>F</mi><mi>b</mi><mi>a</mi><mi>s</mi><mi>e</mi><mi>l</mi><mi>i</mi><mi>n</mi><mi>e</mi><mtext> </mtext><mi mathvariant="normal">/</mi><mtext> </mtext><mi mathvariant="normal">∣</mi><mi mathvariant="normal">∣</mi><mi>B</mi><mi mathvariant="normal">∣</mi><mi mathvariant="normal">∣</mi><mi>i</mi><mi>n</mi><mi>d</mi><mi>e</mi><mi>x</mi><mi>O</mi><mi>f</mi><mi>F</mi><mi>b</mi><mi>a</mi><mi>s</mi><mi>e</mi><mi>l</mi><mi>i</mi><mi>n</mi><mi>e</mi></mrow><annotation encoding="application/x-tex">||BP-LU|| indexOf F baseline \,/\,||B|| indexOf F baseline </annotation></semantics></math>∣∣BP−LU∣∣indexOfFbaseline/∣∣B∣∣indexOfFbaseline contains an object of type line.$

In this example, the relative error of the incomplete LU factorization with threshold dropping is on the same order of the drop tolerance (which does not always occur).

Use an incomplete LU factorization as a preconditioner for bicgstab to solve a linear system.

Load west0479, a real 479-by-479 nonsymmetric sparse matrix.

load west0479 A = west0479;

Define b so that the true solution to Ax=b is a vector of all ones.

Set the tolerance and maximum number of iterations.

Use bicgstab to find a solution at the requested tolerance and number of iterations. Specify five outputs to return information about the solution process:

x is the computed solution to A*x = b.
fl0 is a flag indicating whether the algorithm converged.
rr0 is the relative residual of the computed answer x.
it0 is the iteration number when x was computed.
rv0 is a vector of the residual history at each half iteration for ‖b-Ax‖.

[x,fl0,rr0,it0,rv0] = bicgstab(A,b,tol,maxit); fl0

fl0 is 1 because bicgstab does not converge to the requested tolerance 1e-12 within the requested 20 iterations. In fact, the behavior of bicgstab is so poor that the initial guess x0 = zeros(size(A,2),1) is the best solution and is returned, as indicated by it0 = 0.

To aid with the slow convergence, you can specify a preconditioner matrix. Because A is nonsymmetric, use ilu to generate the preconditioner M=L U. Specify a drop tolerance to ignore nondiagonal entries with values smaller than 1e-6. Solve the preconditioned system A M-1 M x=b by specifying L and U as inputs to bicgstab.

options = struct("type","ilutp","droptol",1e-6); [L,U] = ilu(A,options); [x_precond,fl1,rr1,it1,rv1] = bicgstab(A,b,tol,maxit,L,U); fl1

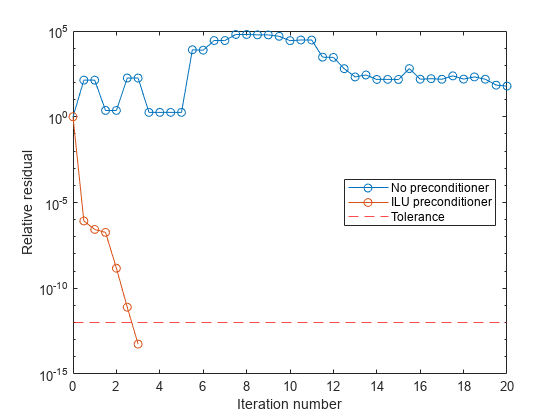
The use of an ilu preconditioner produces a relative residual rr1 less than the requested tolerance of 1e-12 at the third iteration. The output rv1(1) is norm(b), and the output rv1(end) is norm(b-A*x1).

You can follow the progress of bicgstab by plotting the relative residuals at each half iteration. Plot the residual history of each solution with a line for the specified tolerance.

semilogy((0:numel(rv0)-1)/2,rv0/norm(b),"-o") hold on semilogy((0:numel(rv1)-1)/2,rv1/norm(b),"-o") yline(tol,"r--"); legend("No preconditioner","ILU preconditioner","Tolerance",Location="East") xlabel("Iteration number") ylabel("Relative residual")

Figure contains an axes object. The axes object with xlabel Iteration number, ylabel Relative residual contains 3 objects of type line, constantline. These objects represent No preconditioner, ILU preconditioner, Tolerance.

Input Arguments

collapse all

Input matrix, specified as a sparse square matrix.

Data Types: single | double
Complex Number Support: Yes

LU factorization options, specified as a structure with up to five fields:

Field Name	Summary	Description
type	Type of incomplete LU factorization	Valid values for type are: "nofill"(default) — Perform ILU factorization with 0 level of fill in, known as ILU(0). With type set to"nofill", only the milu option is used; all other fields are ignored."crout" — Perform the Crout version of ILU factorization, known as ILUC. With type set to"crout", only the droptol andmilu options are used; all other fields are ignored."ilutp" — Perform ILU factorization with threshold and pivoting, known as ILUTP. Pivoting is performed only with this type.The default value is"nofill".
droptol	Drop tolerance of the incomplete LU factorization	Valid value for droptol is any nonnegative scalar. The nonzero entries of U satisfyabs(U(i,j)) >= droptolnorm(A(:,j)), with the exception of the diagonal entries, which are retained regardless of if they satisfy this criterion. The entries of L are tested against the local drop tolerance before being scaled by the pivot, so the nonzero entries of L satisfy abs(L(i,j)) >= droptolnorm(A(:,j))/U(j,j).The default value is0, which produces the complete LU factorization.
milu	Type of modified incomplete LU factorization	Valid values for milu are: "off" — No modified incomplete LU factorization is produced."row" — Produce the row-sum modified incomplete LU factorization. The diagonal elements of the upper triangular factor U are compensated so that row sums of the original matrix are preserved. That is, Ae = LUe, where e is the column vector of ones. "col" — Produce the column-sum modified incomplete LU factorization. The diagonal elements of the upper triangular factor U are compensated so that column sums of the original matrix are preserved. That is, e'A = e'LU.The default value is "off".
udiag	Whether to replace zero diagonal entries of U	Valid values for udiag are 0 and 1. If udiag is1, then any zero diagonal entries of the upper triangular factor U are replaced by the local drop tolerance in an attempt to avoid a singular factor.The default value is 0.
thresh	Pivot threshold	Valid values are between 0, where the algorithm selects the diagonal pivot, and 1, where the algorithm chooses the maximum magnitude entry in the column to be the pivot. Pivoting occurs when the diagonal entry in a column has a magnitude less thanthresh times the magnitude of any subdiagonal entry in that column.The default value is1.

Output Arguments

collapse all

Lower triangular factor, returned as a sparse square matrix.

When options.type is specified as"nofill" (by default) or "crout",L is returned as a unit lower triangular matrix (that is, a lower triangular matrix with 1s on the main diagonal).
When options.type is specified as"ilutp" and options.milu is specified as"col", L is returned as a row-permuted unit lower triangular matrix.

Upper triangular factor, returned as a sparse square matrix.

When options.type is specified as"nofill" (by default) or "crout",U is returned as an upper triangular matrix.
When options.type is specified as"ilutp" and options.milu is specified as"row", U is returned as a column-permuted upper triangular matrix.

Permutation matrix, returned as a sparse square matrix.

When options.type is specified as "nofill" (by default) or "crout", P is returned as an identity matrix of the same size as A because neither of these types performs pivoting.

Nonzeros of the LU factors, returned as a sparse square matrix, where W = L + U - speye(size(A)).

Tips

The incomplete factorizations returned by this function may be useful as preconditioners for a system of linear equations being solved by iterative methods, such as bicg, bicgstab, or gmres.

References

[1] Saad, Y. "Preconditioning Techniques", chap. 10 in Iterative Methods for Sparse Linear Systems. The PWS Series in Computer Science. Boston: PWS Pub. Co, 1996.

Version History

Introduced in R2007a

expand all

You can specify the input matrix A as single precision. IfA is single, the output arguments are alsosingle.