optimvalues - Create values for optimization problem - MATLAB (original) (raw)
Create values for optimization problem
Since R2022a
Syntax
Description
[val](#mw%5F50ec440d-9f92-4185-b258-12b34ed5fd5e) = optimvalues([prob](#mw%5F970b5cff-3e58-4554-bd85-d65b0f11e2c9),[dataname](#mw%5Fe174ae86-d1ea-41eb-9548-0886ad956b64)1,dataval1,...) creates an OptimizationValues object for the problem prob. Specify all variable names and their associated values, and optionally objective or constraint values, by using name-value arguments. For example, to specify that x takes odd values from 1 through 99,
val = optimvalues(prob,x=1:2:99);
Use val as an initial point or initial population forprob.
Examples
To create initial points for ga (genetic algorithm solver) in the problem-based approach, create an OptimizationValues object using optimvalues.
Create optimization variables for a 2-D problem with Rosenbrock's function as the fitness (objective) function.
x = optimvar("x",LowerBound=-5,UpperBound=5); y = optimvar("y",LowerBound=-5,UpperBound=5); rosenbrock = (10*(y - x.^2)).^2 + (1-x).^2; prob = optimproblem(Objective=rosenbrock);
Create 100 random 2-D points within the bounds. The points must be row vectors.
rng default % For reproducibility xval = -5 + 10rand(1,100); yval = -5 + 10rand(1,100);
Create the initial point values object. Because you do not calculate the fitness values, the values appear as NaN in the display.
vals = optimvalues(prob,x=xval,y=yval)
vals = 1×100 OptimizationValues vector with properties:
Variables properties: x: [3.1472 4.0579 -3.7301 4.1338 1.3236 -4.0246 -2.2150 0.4688 4.5751 4.6489 -3.4239 4.7059 4.5717 -0.1462 3.0028 -3.5811 -0.7824 4.1574 2.9221 4.5949 1.5574 -4.6429 3.4913 4.3399 1.7874 2.5774 2.4313 -1.0777 1.5548 -3.2881 … ] (1×100 double) y: [-3.3782 2.9428 -1.8878 0.2853 -3.3435 1.0198 -2.3703 1.5408 1.8921 2.4815 -0.4946 -4.1618 -2.7102 4.1334 -3.4762 3.2582 0.3834 4.9613 -4.2182 -0.5732 -3.9335 4.6190 -4.9537 2.7491 3.1730 3.6869 -4.1556 -1.0022 -2.4013 … ] (1×100 double)
Objective properties: Objective: [NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN … ] (1×100 double)
Solve the problem using ga starting from the initial point vals. Set ga options to have a population of 100.
opts = optimoptions("ga",PopulationSize=100); [sol,fv] = solve(prob,vals,Solver="ga",Options=opts)
Solving problem using ga. ga stopped because it exceeded options.MaxGenerations.
sol = struct with fields: x: 1.0551 y: 1.1133
ga returns a solution very near the true solution x = 1, y = 1 with a fitness value near 0.
To create initial points for surrogateopt in the problem-based approach, create an OptimizationValues object using optimvalues.
Create optimization variables for a 2-D problem with Rosenbrock's function as the objective function.
x = optimvar("x",LowerBound=-5,UpperBound=5); y = optimvar("y",LowerBound=-5,UpperBound=5); rosenbrock = (10*(y - x.^2)).^2 + (1 - x).^2; prob = optimproblem(Objective=rosenbrock);
Create constraints that the solution is in a disc of radius 2 about the origin and lies below the line y = 1 + x.
disc = x^2 + y^2 <= 2^2; prob.Constraints.disc = disc; line = y <= 1 + x; prob.Constraints.line = line;
Create 40 random 2-D points within the bounds. The points must be row vectors.
rng default % For reproducibility N = 40; xval = -5 + 10rand(1,N); yval = -5 + 10rand(1,N);
Evaluate Rosenbrock's function on the random points. The function values must be a row vector. This step is optional. If you do not provide the function values, surrogateopt evaluates the objective function at the points (xval,yval). When you have the function values, you can save time for the solver by providing the values as data.
fval = zeros(1,N); for i = 1:N p0 = struct('x',xval(i),'y',yval(i)); fval(i) = evaluate(rosenbrock,p0); end
Evaluate the constraints on the points. The constraint values must be row vectors. This step is optional. If you do not provide the constraint values, surrogateopt evaluates the constraint functions at the points (xval,yval).
discval = zeros(1,N); lineval = zeros(1,N); for i = 1:N p0 = struct('x',xval(i),'y',yval(i)); discval(i) = infeasibility(disc,p0); lineval(i) = infeasibility(line,p0); end
Create the initial point values object.
vals = optimvalues(prob,x=xval,y=yval,Objective=fval,disc=discval,line=lineval)
vals = 1×40 OptimizationValues vector with properties:
Variables properties: x: [3.1472 4.0579 -3.7301 4.1338 1.3236 -4.0246 -2.2150 0.4688 4.5751 4.6489 -3.4239 4.7059 4.5717 -0.1462 3.0028 -3.5811 -0.7824 4.1574 2.9221 4.5949 1.5574 -4.6429 3.4913 4.3399 1.7874 2.5774 2.4313 -1.0777 1.5548 -3.2881 … ] (1×40 double) y: [-0.6126 -1.1844 2.6552 2.9520 -3.1313 -0.1024 -0.5441 1.4631 2.0936 2.5469 -2.2397 1.7970 1.5510 -3.3739 -3.8100 -0.0164 4.5974 -1.5961 0.8527 -2.7619 2.5127 -2.4490 0.0596 1.9908 3.9090 4.5929 0.4722 -3.6138 -3.5071 … ] (1×40 double)
Objective properties: Objective: [1.1067e+04 3.1166e+04 1.2698e+04 1.9992e+04 2.3846e+03 2.6593e+04 2.9811e+03 154.8722 3.5498e+04 3.6362e+04 1.9515e+04 4.1421e+04 3.7452e+04 1.1541e+03 1.6457e+04 1.6510e+04 1.5914e+03 3.5654e+04 5.9109e+03 5.7015e+04 … ] (1×40 double)
Constraints properties: disc: [6.2803 13.8695 16.9638 21.8023 7.5568 12.2078 1.2024 0 21.3146 24.0987 12.7394 21.3751 19.3057 7.4045 19.5331 8.8248 17.7486 15.8313 5.2656 24.7413 4.7390 23.5542 8.1927 18.7982 14.4752 23.7379 2.1343 10.2207 10.7168 … ] (1×40 double) line: [0 0 5.3853 0 0 2.9222 0.6709 0 0 0 0.1841 0 0 0 0 2.5648 4.3798 0 0 0 0 1.1938 0 0 1.1217 1.0155 0 0 0 0 0.3467 1.2245 4.3736 0.9735 7.3213 0 0 0 0 3.3884]
Solve the problem using surrogateopt starting from the initial point vals.
[sol,fv] = solve(prob,vals,Solver="surrogateopt")
Solving problem using surrogateopt.
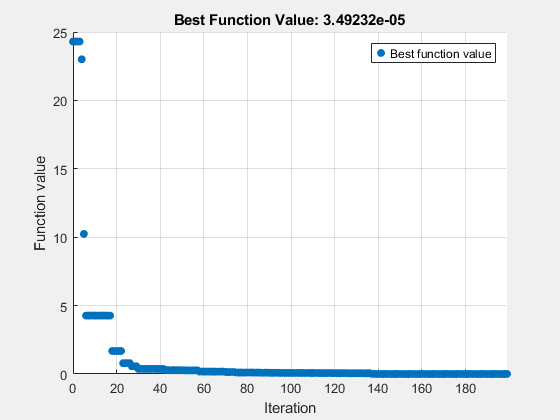
surrogateopt stopped because it exceeded the function evaluation limit set by 'options.MaxFunctionEvaluations'.
sol = struct with fields: x: 1.0031 y: 1.0057
surrogateopt returns a solution somewhat near the true solution x = 1, y = 1 with an objective function value near 0.
Input Arguments
Optimization problem, specified as an OptimizationProblem object. Create prob using optimproblem.
To obtain useful output from optimvalues, you must also include some data in name-value arguments.
Name-Value Arguments
Specify optional pairs of arguments asName1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.
Example: val = optimvalues(x=xvals,y=yvals)
Data for a variable, named objective, or named constraint, specified as a real double array. Specify all data names for the variables. The objective and constraint function names are optional.
When you specify nval points, the values for eachdataname argument must have the following dimensions.
| prob.property.name | size(value) |
|---|---|
| Scalar or vector | numel(prob.property.name)-by-nval |
| Matrix or array | size(prob.property.name)-by-nval |
In particular, if dataname is a vector, the value of thedataname argument is a matrix with nval columns. For example, if the 'x' variable is a row vector of length 2, and nval is 3, then the 'x' variable specification might be:
val = optimvalues(prob,'x',[1 2 3; 4 5 -6]);
This specification means that 'x' takes the three values[1,4], [2,5], and[3,-6].
Example: For scalar 'x' and two-element row vector'y' with nval = 2: val = optimvalues(prob,x=[5,3],y=[1 2;3 4]). The output val has two values: x = 5, y = [1 3] and x = 3, y = [2 4].
Data Types: double
Values for an unnamed objective function, specified as a real double array. The size of the values is the same as in dataname.
You can specify values of multiple objective functions for optimization problems in two ways:
- The
Objectiveproperty of the optimization problem is a function handle, where the function returns a vector or array. In this case, specify the value as a matrix. Each matrix row represents the values of one objective at the various points. Each column represents the values of the various objectives at one point. - The
Objectiveproperty of the optimization problem has multiple named objectives. In this case, specify the values for each named objective using its name as adatanameargument.
These solvers use any supplied objective function values:
gagamultiobjparetosearchparticleswarmsurrogateopt
Example: For one objective and two points, val = optimvalues(prob,x=[3,5],Objective=[exp(3)+1,exp(5)-1])
Data Types: double
Values for an unnamed constraint function, specified as a real double array. The size of the values is the same as in dataname.
You can specify values of multiple constraint functions for optimization problems in two ways:
- The
Constraintsproperty of the optimization problem is a function handle, where the function returns an array. In this case, specify the values as an array with one more dimension than the function returns. - The
'Constraints'property of the optimization problem has multiple named constraints. In this case, specify the values for each named constraint using its name as adatanameargument.
These solvers use any supplied nonlinear constraint function values:
paretosearchsurrogateopt
These solvers ensure that linear constraints are satisfied at all iterations or for all population members:
gagamultiobjparetosearchpatternsearchsurrogateopt
Example: For two points and three constraints, val = optimvalues(prob,x=[3,5],Objective=[exp(3)+1,exp(5)-1],Constraints=[4 5;-7 -2;0.2 12])
Data Types: double
Output Arguments
Point and function values, returned as a vector of OptimizationValues objects. The vector has nval entries, where nval is the number of points in val.
Version History
Introduced in R2022a
Use optimvalues to specify initial objective function values forparticleswarm in the problem-based approach. For example,
x = optimvar("x",1,2,LowerBound=[1 2],UpperBound=[11 13]); fun = sum(exp(x)); prob = optimproblem("Objective",fun); x0 = [3;5] + 7*rand([2 20]); % Twenty initial points val = optimvalues(prob,x=x0,Objective=sum(exp(x0),1)); % Twenty initial values sol = solve(prob,val,Solver="particleswarm")