Linear Algebra tutorial: Singular value decomposition (SVD) (original) (raw)
Singular value decomposition (SVD) is a factorization of a rectangular matrix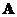 
into three matrices
, 
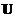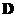and
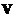. The two matrices 
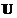and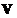 
are orthogonal matrices (
,
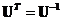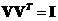) while 
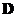is a diagonal matrix. The factorization means that we can multiply the three matrices to get back the original matrix
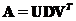. The transpose matrix is obtained through
.
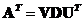Since both orthogonal matrix and diagonal matrix have many nice properties, SVD is one of the most powerful matrix decomposition that used in many applications such as least square (regression), feature selection (PCA, MDS), spectral clustering, image restoration and 3D computer vision (Fundamental matrix estimation), equilibrium of Markov Chain, and many others.
Matrices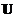 
and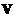 
are not unique, their columns come from the concatenation of eigenvectors of symmetric matrices 
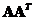and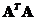
. Since eigenvectors of symmetric matrix are orthogonal (and linearly independent), they can be used as basis vectors (coordinate system) to span a multidimensional space. The absolute value of the determinant of orthogonal matrix is one, thus the matrix always has inverse. Furthermore, each column (and each row) of orthogonal matrix has unit norm.
The diagonal matrix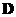 
contains the square of eigenvalues of symmetric matrix
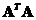. The diagonal elements are non-negative numbers and they are called singular values. Because they come from a symmetric matrix, the eigenvalues (and the eigenvectors) are all real numbers (no complex numbers).
Numerical computation of SVD is stable in term of round off error. When some of the singular values are nearly zero, we can truncate them as zero and it yields numerical stability.
Example:
Find SVD of matrix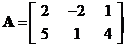
.
Solution:
First, we multiply the matrix 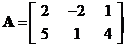by its transpose to produce symmetric matrices
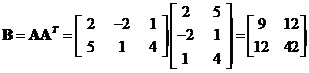and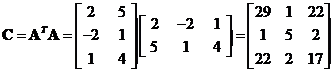
.
Then we find the eigenvalues and eigenvectors of the symmetric matrices. For matrix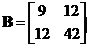
, the eigenvalues are 
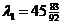and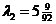
. The corresponding eigenvectors are
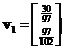and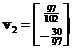 
respectively. Concatenating the eigenvectors produces matrix
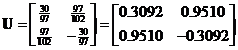. The diagonal matrix can be obtained from the square root of the eigenvalues
.
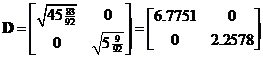For matrix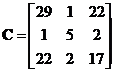
, the eigenvalues are 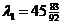and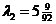. The third eigenvalue is zero as expected because the eigenvalues of 
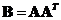are exactly the same as the eigenvalues of matrix
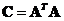. The corresponding eigenvectors are
, 
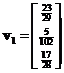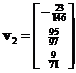and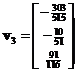 
respectively. Concatenating the eigenvectors produces matrix
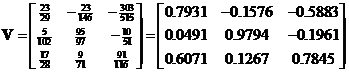. Since the Singular Value Decomposition factor matrix
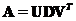, the diagonal matrix can also be obtained from
.
Remember, the eigenvectors are actually the many solutions of homogeneous equation. They are not unique and correct up to a scalar multiple. Thus, you can multiply an eigenvector with -1 and will still get the same correct result.
The interactive program below produces the factorization of a rectangular matrix using Singular Value Decomposition (SVD). You can also truncate the results by setting lower singular values to zero. This feature is useful for feature selection (such as PCA and MDS). Random example button will generate random rectangular matrix. Try to experiment with your own input matrix.
Yes, this program is a free educational program!! Please don't forget to tell your friends and teacher about this awesome program!
Properties
In one strike, Singular Value Decomposition (SVD) can reveal many things:
See also: Matrix Eigen Value & Eigen Vector for Symmetric Matrix, Similarity and Matrix Diagonalization, Symmetric Matrix, Spectral Decomposition
Rate this tutorial or give your comments about this tutorial
Preferable reference for this tutorial is
Teknomo, Kardi (2011) Linear Algebra tutorial. https:\\people.revoledu.com\kardi\tutorial\LinearAlgebra\