Rect - PyMuPDF 1.26.1 documentation (original) (raw)
Toggle table of contents sidebar
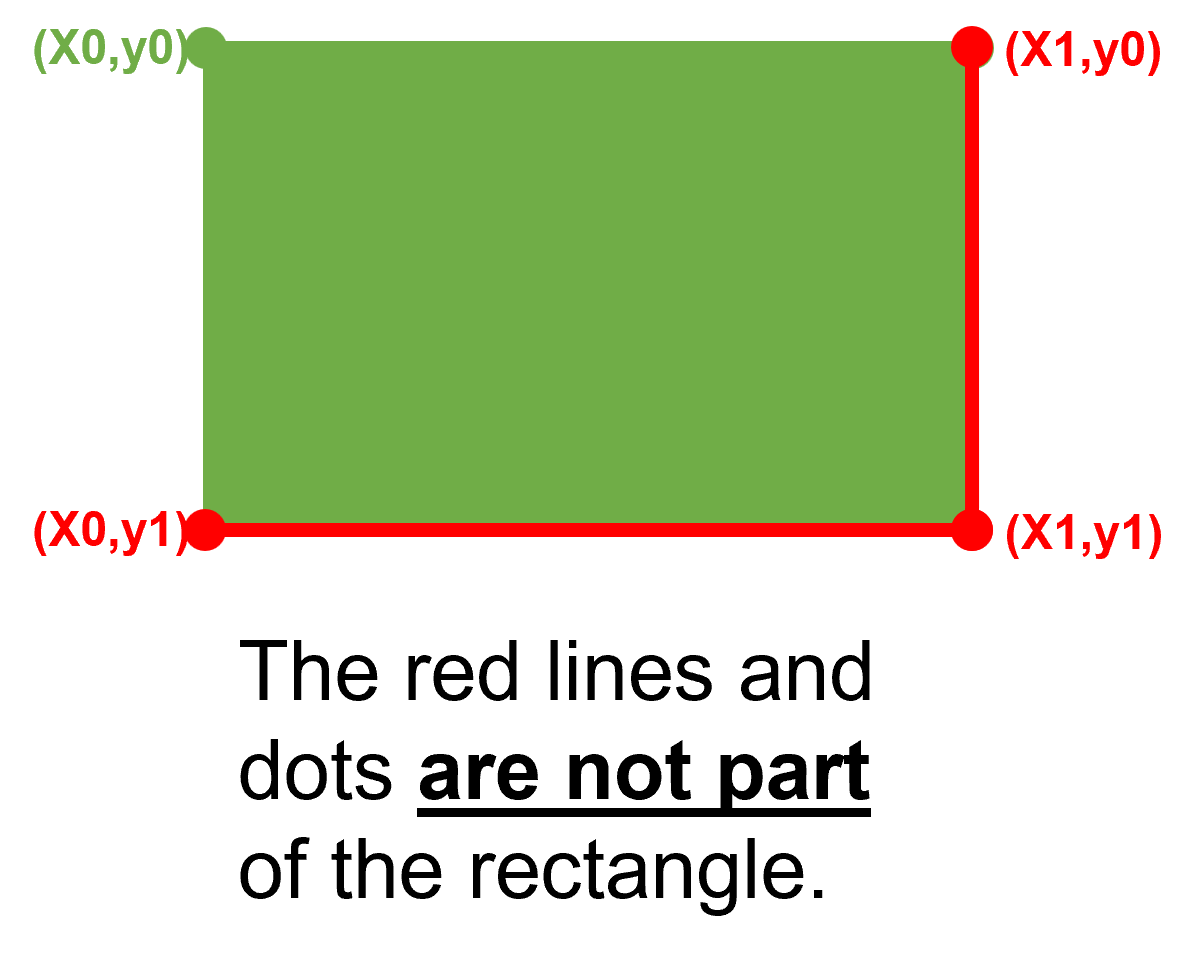
Rect represents a rectangle defined by four floating point numbers x0, y0, x1, y1. They are treated as being coordinates of two diagonally opposite points. The first two numbers are regarded as the “top left” corner P(x0,y0) and P(x1,y1) as the “bottom right” one. However, these two properties need not coincide with their intuitive meanings – read on.
The following remarks are also valid for IRect objects:
- A rectangle in the sense of (Py-) MuPDF (and PDF) always has borders parallel to the x- resp. y-axis. A general orthogonal tetragon is not a rectangle – in contrast to the mathematical definition.
- The constructing points can be (almost! – see below) anywhere in the plane – they need not even be different, and e.g. “top left” need not be the geometrical “north-western” point.
- Units are in points, where 72 points is 1 inch.
- For any given quadruple of numbers, the geometrically “same” rectangle can be defined in four different ways:
- Rect(P(x0,y0), P(x1,y1))
- Rect(P(x1,y1), P(x0,y0))
- Rect(P(x0,y1), P(x1,y0))
- Rect(P(x1,y0), P(x0,y1))
(Changed in v1.19.0) Hence some classification:
- A rectangle is called valid if
x0 <= x1andy0 <= y1(i.e. the bottom right point is “south-eastern” to the top left one), otherwise invalid. Of the four alternatives above, only the first is valid. Please take into account, that in MuPDF’s coordinate system, the y-axis is oriented from top to bottom. Invalid rectangles have been called infinite in earlier versions. - A rectangle is called empty if
x0 >= x1ory0 >= y1. This implies, that invalid rectangles are also always empty. And width (resp. height) is set to zero ifx0 > x1(resp.y0 > y1). In previous versions, a rectangle was empty only if one of width or height was zero. - Rectangle coordinates cannot be outside the number range from
FZ_MIN_INF_RECT = -2147483648toFZ_MAX_INF_RECT = 2147483520. Both values have been chosen, because they are the smallest / largest 32bit integers that survive C float conversion roundtrips. In previous versions there was no limit for coordinate values. - There is exactly one “infinite” rectangle, defined by
x0 = y0 = FZ_MIN_INF_RECTandx1 = y1 = FZ_MAX_INF_RECT. It contains every other rectangle. It is mainly used for technical purposes – e.g. when a function call should ignore a formally required rectangle argument. This rectangle is not empty. - Rectangles are (semi-) open: The right and the bottom edges (including the resp. corners) are not considered part of the rectangle. This implies, that only the top-left corner
(x0, y0)can ever belong to the rectangle - the other three corners never do. An empty rectangle contains no corners at all. - Here is an overview of the changes.
Notion Versions < 1.19.0 Versions 1.19.* empty x0 = x1 or y0 = y1 x0 >= x1 or y0 >= y1 – includes invalid rects valid n/a x0 <= x1 and y0 <= y1 infinite all rects where x0 > x1 or y1 > y0 exactly one infinite rect / irect! coordinate values all numbers FZ_MIN_INF_RECT <= number <= FZ_MAX_INF_RECT borders, corners are parts of the rectangle right and bottom corners and edges are outside - There are new top level functions defining infinite and standard empty rectangles and quads, see INFINITE_RECT() and friends.
| Methods / Attributes | Short Description |
|---|---|
| Rect.contains() | checks containment of point_likes and rect_likes |
| Rect.get_area() | calculate rectangle area |
| Rect.include_point() | enlarge rectangle to also contain a point |
| Rect.include_rect() | enlarge rectangle to also contain another one |
| Rect.intersect() | common part with another rectangle |
| Rect.intersects() | checks for non-empty intersections |
| Rect.morph() | transform with a point and a matrix |
| Rect.torect() | the matrix that transforms to another rectangle |
| Rect.norm() | the Euclidean norm |
| Rect.normalize() | makes a rectangle valid |
| Rect.round() | create smallest IRect containing rectangle |
| Rect.transform() | transform rectangle with a matrix |
| Rect.bottom_left | bottom left point, synonym bl |
| Rect.bottom_right | bottom right point, synonym br |
| Rect.height | rectangle height |
| Rect.irect | equals result of method round() |
| Rect.is_empty | whether rectangle is empty |
| Rect.is_valid | whether rectangle is valid |
| Rect.is_infinite | whether rectangle is infinite |
| Rect.top_left | top left point, synonym tl |
| Rect.top_right | top_right point, synonym tr |
| Rect.quad | Quad made from rectangle corners |
| Rect.width | rectangle width |
| Rect.x0 | left corners’ x coordinate |
| Rect.x1 | right corners’ x -coordinate |
| Rect.y0 | top corners’ y coordinate |
| Rect.y1 | bottom corners’ y coordinate |
Class API
class Rect#
__init__(self)#
__init__(self, x0, y0, x1, y1)#
__init__(self, top_left, bottom_right)#
__init__(self, top_left, x1, y1)#
__init__(self, x0, y0, bottom_right)#
__init__(self, rect)#
__init__(self, sequence)#
Overloaded constructors: top_left, bottom_right stand for point_like objects, “sequence” is a Python sequence type of 4 numbers (see Using Python Sequences as Arguments in PyMuPDF), “rect” means another rect_like, while the other parameters mean coordinates.
If “rect” is specified, the constructor creates a new copy of it.
Without parameters, the empty rectangle Rect(0.0, 0.0, 0.0, 0.0) is created.
round()#
Creates the smallest containing IRect. This is not the same as simply rounding the rectangle’s edges: The top left corner is rounded upwards and to the left while the bottom right corner is rounded downwards and to the right.
pymupdf.Rect(0.5, -0.01, 123.88, 455.123456).round() IRect(0, -1, 124, 456)
- If the rectangle is empty, the result is also empty.
- Possible paradox: The result may be empty, even if the rectangle is not empty! In such cases, the result obviously does not contain the rectangle. This is because MuPDF’s algorithm allows for a small tolerance (1e-3). Example:
r = pymupdf.Rect(100, 100, 200, 100.001) r.is_empty # rect is NOT empty False r.round() # but its irect IS empty! pymupdf.IRect(100, 100, 200, 100) r.round().is_empty True
Return type:
transform(m)#
Transforms the rectangle with a matrix and replaces the original. If the rectangle is empty or infinite, this is a no-operation.
Parameters:
m (matrix_like) – The matrix for the transformation.
Return type:
Rect
Returns:
the smallest rectangle that contains the transformed original.
intersect(r)#
The intersection (common rectangular area, largest rectangle contained in both) of the current rectangle and r is calculated and replaces the current rectangle. If either rectangle is empty, the result is also empty. If r is infinite, this is a no-operation. If the rectangles are (mathematically) disjoint sets, then the result is invalid. If the result is valid but empty, then the rectangles touch each other in a corner or (part of) a side.
Parameters:
r (rect_like) – Second rectangle
include_rect(r)#
The smallest rectangle containing the current one and r is calculated and replaces the current one. If either rectangle is infinite, the result is also infinite. If r is empty, the current rectangle remains unchanged. Else if the current rectangle is empty, it is replaced by r.
Parameters:
r (rect_like) – Second rectangle
include_point(p)#
The smallest rectangle containing the current one and point_like p is calculated and replaces the current one. The infinite rectangle remains unchanged. To create the rectangle that wraps a sequence of points, start with EMPTY_RECT() and successively include the members of the sequence.
Parameters:
p (point_like) – Point to include.
get_area([_unit_])#
Calculate the area of the rectangle and, with no parameter, equals abs(rect). Like an empty rectangle, the area of an infinite rectangle is also zero. So, at least one of pymupdf.Rect(p1, p2) and pymupdf.Rect(p2, p1) has a zero area.
Parameters:
unit (str) – Specify required unit: respective squares of px (pixels, default), in (inches), cm (centimeters), or mm (millimeters).
Return type:
float
contains(x)#
Checks whether x is contained in the rectangle. It may be an IRect, Rect, Point or number. If x is an empty rectangle, this is always true. If the rectangle is empty this is always False for all non-empty rectangles and for all points. x in rect and rect.contains(x) are equivalent.
Parameters:
x (rect_like or point_like.) – the object to check.
Return type:
bool
intersects(r)#
Checks whether the rectangle and a rect_like “r” contain a common non-empty Rect. This will always be False if either is infinite or empty.
Parameters:
r (rect_like) – the rectangle to check.
Return type:
bool
torect(rect)#
- New in version 1.19.3
Compute the matrix which transforms this rectangle to a given one.
Parameters:
rect (rect_like) – the target rectangle. Must not be empty or infinite.
Return type:
Returns:
a matrix mat such that self * mat = rect. Can for example be used to transform between the page and the pixmap coordinates. See an example use here How to Use Pixmaps: Checking Text Visibility.
morph(fixpoint, matrix)#
- New in version 1.17.0
Return a new quad after applying a matrix to the rectangle using the fixed point fixpoint.
Parameters:
- fixpoint (point_like) – the fixed point.
- matrix (matrix_like) – the matrix.
Returns:
a new Quad. This a wrapper for the same-named quad method. If infinite, the infinite quad is returned.
norm()#
- New in version 1.16.0
Return the Euclidean norm of the rectangle treated as a vector of four numbers.
normalize()#
Replace the rectangle with its valid version. This is done by shuffling the rectangle corners. After completion of this method, the bottom right corner will indeed be south-eastern to the top left one (but may still be empty).
irect#
Equals result of method round().
top_left#
tl#
Equals Point(x0, y0).
Type:
top_right#
tr#
Equals Point(x1, y0).
Type:
bottom_left#
bl#
Equals Point(x0, y1).
Type:
bottom_right#
br#
Equals Point(x1, y1).
Type:
quad#
The quadrilateral Quad(rect.tl, rect.tr, rect.bl, rect.br).
Type:
width#
Width of the rectangle. Equals max(x1 - x0, 0).
Return type:
float
height#
Height of the rectangle. Equals max(y1 - y0, 0).
Return type:
float
x0#
X-coordinate of the left corners.
Type:
float
y0#
Y-coordinate of the top corners.
Type:
float
x1#
X-coordinate of the right corners.
Type:
float
y1#
Y-coordinate of the bottom corners.
Type:
float
is_infinite#
True if this is the infinite rectangle.
Type:
bool
is_empty#
True if rectangle is empty.
Type:
bool
is_valid#
True if rectangle is valid.
Type:
bool
Note
- This class adheres to the Python sequence protocol, so components can be accessed via their index, too. Also refer to Using Python Sequences as Arguments in PyMuPDF.
- Rectangles can be used with arithmetic operators – see chapter Operator Algebra for Geometry Objects.