arviz.plot_bf — ArviZ dev documentation (original) (raw)

arviz.plot_bf(idata, var_name, prior=None, ref_val=0, colors=('C0', 'C1'), figsize=None, textsize=None, hist_kwargs=None, plot_kwargs=None, ax=None, backend=None, backend_kwargs=None, show=None)[source]#

Approximated Bayes Factor for comparing hypothesis of two nested models.

The Bayes factor is estimated by comparing a model (H1) against a model in which the parameter of interest has been restricted to be a point-null (H0). This computation assumes the models are nested and thus H0 is a special case of H1.

Parameters:

idataInferenceData

Any object that can be converted to an arviz.InferenceData object Refer to documentation of arviz.convert_to_dataset() for details.

var_namestr, optional

Name of variable we want to test.

priornumpy.array, optional

In case we want to use different prior, for example for sensitivity analysis.

ref_valint, default 0

Point-null for Bayes factor estimation.

colorstuple, default (‘C0’, ‘C1’)

Tuple of valid Matplotlib colors. First element for the prior, second for the posterior.

figsize(float, float), optional

Figure size. If None it will be defined automatically.

textsizefloat, optional

Text size scaling factor for labels, titles and lines. If None it will be auto scaled based on figsize.

plot_kwargsdict, optional

Additional keywords passed to matplotlib.pyplot.plot().

hist_kwargsdict, optional

Additional keywords passed to arviz.plot_dist(). Only works for discrete variables.

axaxes, optional

matplotlib.axes.Axes or bokeh.plotting.Figure.

backend{“matplotlib”, “bokeh”}, default “matplotlib”

Select plotting backend.

backend_kwargsdict, optional

These are kwargs specific to the backend being used, passed tomatplotlib.pyplot.subplots() or bokeh.plotting.figure. For additional documentation check the plotting method of the backend.

showbool, optional

Call backend show function.

Returns:

dictA dictionary with BF10 (Bayes Factor 10 (H1/H0 ratio), and BF01 (H0/H1 ratio).

axesmatplotlib Axes or Bokeh Figure

Notes

The bayes Factor is approximated as the Savage-Dickey density ratio algorithm presented in [1].

References

[1]

Heck, D., 2019. A caveat on the Savage-Dickey density ratio: The case of computing Bayes factors for regression parameters.

Examples

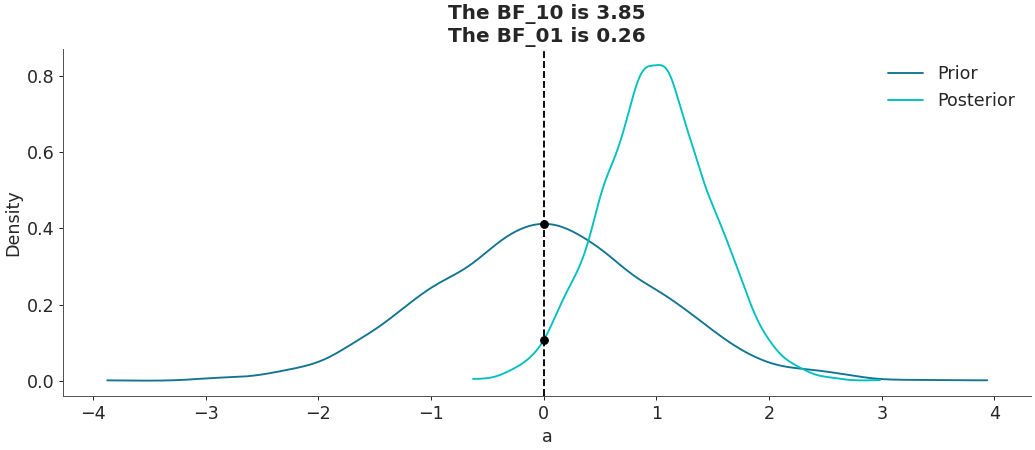
Moderate evidence indicating that the parameter “a” is different from zero.

import numpy as np import arviz as az idata = az.from_dict(posterior={"a":np.random.normal(1, 0.5, 5000)}, ... prior={"a":np.random.normal(0, 1, 5000)}) az.plot_bf(idata, var_name="a", ref_val=0)