dsp.Differentiator - Direct form FIR fullband differentiator filter - MATLAB (original) (raw)

Direct form FIR fullband differentiator filter

Description

The dsp.Differentiator System object™ applies a fullband differentiator filter on the input signal to differentiate all its frequency components. This object uses an FIR equiripple filter design to design the differentiator filter. The ideal frequency response of the differentiator is D(ω)=jω for −π≤ω≤π. You can design the filter with minimum order with a specified order. This object supports fixed-point operations.

To filter each channel of your input:

Create the dsp.Differentiator object and set its properties.
Call the object with arguments, as if it were a function.

To learn more about how System objects work, see What Are System Objects?

This object supports C/C++ code generation and SIMD code generation under certain conditions. For more information, see Code Generation.

Creation

Syntax

Description

`DF` = dsp.Differentiator returns a differentiator, DF, which independently filters each channel of the input over time using the given design specifications.

example

`DF` = dsp.Differentiator(`Name=Value`) sets properties using one or more name-value arguments. For example, to specify the order of the filter as 15, setFilterOrder to 15.

Properties

expand all

Unless otherwise indicated, properties are nontunable, which means you cannot change their values after calling the object. Objects lock when you call them, and therelease function unlocks them.

If a property is tunable, you can change its value at any time.

For more information on changing property values, seeSystem Design in MATLAB Using System Objects.

Option to design a minimum-order filter, specified as a logical scalar. The filter has 2 degrees of freedom. When you set this property to

true — The object designs the filter with the minimum order that meets the PassbandRipple value.
false — The object designs the filter with order that you specify in the FilterOrder property.

This property is not tunable.

Order of the filter, specified as an odd positive integer.

This property is not tunable.

Dependencies

You can specify the filter order only when"DesignForMinimumOrder" is set tofalse.

Maximum passband ripple in dB, specified as a positive real scalar.

This property is not tunable.

Dependencies

You can specify the passband ripple only when"DesignForMinimumOrder" is set totrue.

Option to scale the filter coefficients, specified as a logical scalar. When you set this property to true, the object scales the filter coefficients to preserve the input dynamic range.

This property is not tunable.

Fixed-Point Properties

Word and fraction lengths of coefficients, specified as a signed or unsignednumerictype object. The default,numerictype(1,16), corresponds to a signed numeric type object with 16-bit coefficients. To give the best possible precision, the fraction length is computed based on the coefficient values.

This property is not tunable.

The word length of the output is the same as the word length of the input. The object computes the fraction length of the output such that the entire dynamic range of the output can be represented without overflow. For details on how the object computes the fraction length of the output, see Fixed-Point Precision Rules for Avoiding Overflow in FIR Filters.

Rounding method for output fixed-point operations, specified as a character vector. For more information on the rounding modes, see Precision and Range.

This property is not tunable.

Usage

Syntax

Description

[y](#d126e266494) = DF([x](#d126e266439)) applies a fullband differentiator filter to the input signal, x.y is a differentiated version of x.

example

Input Arguments

expand all

Data input, specified as a vector or a matrix. If the input signal is a matrix, each column of the matrix is treated as an independent channel. The number of rows in the input signal denotes the channel length. The data type characteristics (double, single, or fixed-point) and the real-complex characteristics (real or complex valued) must be the same for the input data and output data.

Output Arguments

expand all

Differentiated signal, returned as a vector or matrix of the same size, data type, and complexity as the input signal, x.

Object Functions

To use an object function, specify the System object as the first input argument. For example, to release system resources of a System object named obj, use this syntax:

expand all

getFilter	Get underlying FIR filter
outputDelay	Determine output delay of single-rate or multirate filter

step	Run System object algorithm
release	Release resources and allow changes to System object property values and input characteristics
reset	Reset internal states of System object

Examples

collapse all

Estimate the group delay of a linear phase FIR filter using a dsp.TransferFunctionEstimator object followed by dsp.PhaseExtractor and dsp.Differentiator objects. The group delay of a linear phase FIR filter is given by 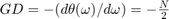$GD = -(d\theta(\omega)/d\omega) = - \frac{N}{2}$ , where 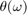$\theta(\omega)$ is the phase information of the filter, $\omega$ is the frequency vector, and N is the order of the filter.

Set Up the Objects

Create a linear phase FIR lowpass filter. Set the order to 200, the passband frequency to 255 Hz, the passband ripple to 0.1 dB, and the stopband attenuation to 80 dB. Specify a sample rate of 512 Hz.

Fs = 512; LPF = dsp.LowpassFilter(SampleRate=Fs,PassbandFrequency=255,... DesignForMinimumOrder=false,FilterOrder=200);

To estimate the transfer function of the lowpass filter, create a transfer function estimator. Specify the window to be Hann. Set the FFT length to 1024 and the number of spectral averages to 200.

TFE = dsp.TransferFunctionEstimator(FrequencyRange="twosided",... SpectralAverages=200,FFTLengthSource="Property",... FFTLength=1024);

To extract the unwrapped phase from the frequency response of the filter, create a phase extractor.

To differentiate the phase 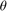$\theta$ , create a differentiator filter. This value is used in computing the group delay.

To smoothen the input, create a variable bandwidth FIR filter.

Gain1 = 512/pi; Gain2 = -1; VBFilter = dsp.VariableBandwidthFIRFilter(CutoffFrequency=10,... SampleRate=Fs);

To view the group delay of the filter, create an array plot object.

AP = dsp.ArrayPlot(PlotType="Line",YLimits=[-500 400],... YLabel="Amplitude",XLabel="Number of samples");

Run the Algorithm

The for-loop is the streaming loop that estimates the group delay of the filter. In the loop, the algorithm filters the input signal, estimates the transfer function of the filter, and differentiates the phase of the filter to compute the group delay.

Niter = 1000; % Number of iterations for k = 1:Niter x = randn(512,1); % Input signal = white Gaussian noise y = LPF(x); % Filter noise with Lowpass FIR filter H = TFE(x,y); % Compute transfer function estimate Phase = PE(H); % Extract the Unwrapped phase phaseaftergain1 = Gain1*Phase; DiffOut = DF(phaseaftergain1); % Differentiate the phase phaseaftergain2 = Gain2 * DiffOut; VBFOut = VBFilter(phaseaftergain2); % Smooth the group delay AP(VBFOut); % Display the group delay end

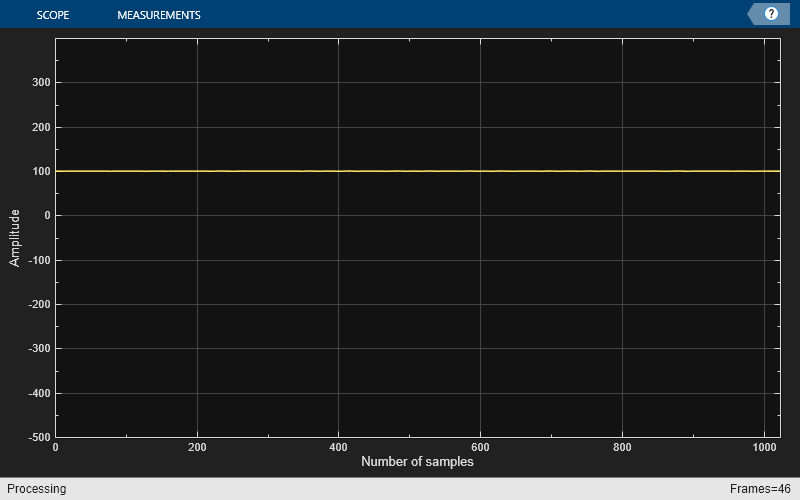
As you can see, the group delay of the lowpass filter is 100.

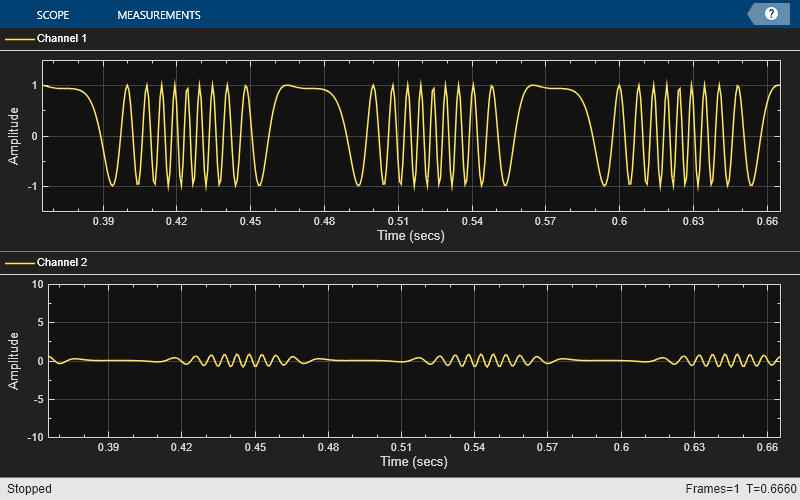
Create an FM wave on a 100 Hz carrier signal sampled at 1.5 kHz.

Fc = 1e2; % Carrier Fs = 1.5e3; % Sample rate sinewave = dsp.SineWave(Frequency=10,... SamplesPerFrame=1e3,... SampleRate=Fs);

Convert the FM signal to an AM signal.

ts = timescope(TimeSpanSource="Property",... TimeSpan=0.3,... BufferLength=10*Fs,... SampleRate=Fs,... ShowGrid=true,... YLimits=[-1.5 1.5],... LayoutDimensions=[2 1]);

df = dsp.Differentiator;

tic while toc<2.2 x = step(sinewave); fm_y = modulate(x,Fc,Fs,"fm"); am_y = step(df,fm_y); step(ts,fm_y,am_y); end

release(df); release(ts);

Algorithms

expand all

Differentiator computes the derivative of a signal. The frequency response of an ideal differentiator filter is given by D(ω)=jω, defined over the Nyquist interval −π≤ω≤π.

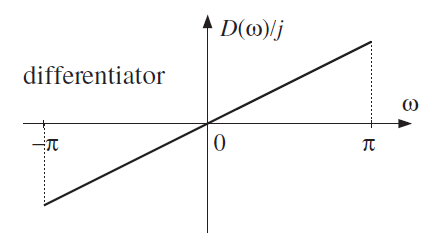
The frequency response is antisymmetric and is linearly proportional to the frequency.

dsp.Differentiator object acts as a differentiator filter. This object condenses the two-step process into one. For the minimum order design, the object uses generalized Remez FIR filter design algorithm. For the specified order design, the object uses the Parks-McClellan optimal equiripple FIR filter design algorithm. The filter is designed as a linear phase Type-IV FIR filter with a Direct form structure.

The ideal differentiator has an antisymmetric impulse response given by d(n)=−d(−n). Hence d(0)=0. The differentiator must have zero response at zero frequency.

Linear-Phase FIR Differentiator Filter

The impulse response of an antisymmetric linear-phase FIR filter is given by h(n)=−h(M−1−n), where M is the length of the filter. Because the filter is antisymmetric, you can use this type of FIR filter to design the linear-phase FIR differentiators.

Consider the design of linear-phase FIR differentiators based on the Chebyshev approximation criterion.

If M is odd, the real-valued frequency response of the FIR filter, Hr(ω), has the characteristics that Hr(0) = 0 and Hr(π) = 0. This filter satisfies the condition of zero response at zero frequency. However, it is not fullband because Hr(π) = 0. This differentiator has a linear response over the limited frequency range [0 2π_fp_], where fp is the bandwidth of the differentiator. The absolute error between the desired response and the Chebyshev approximation increases as ω increases from 0 to 2π_fp_.

If M is even, the real-valued frequency response of the FIR filter, Hr(ω), has the characteristics that Hr(0) = 0 and Hr(π) ≠ 0. This filter satisfies the condition of zero response at zero frequency. It is fullband and this design results in a significantly smaller approximation error than comparable odd-length differentiators. Hence, even-length (odd order) differentiators are preferred in practical systems.

References

[1] Orfanidis, Sophocles J. Introduction to Signal Processing. Upper Saddle River, NJ: Prentice-Hall, 1996.

Extended Capabilities

Version History

Introduced in R2016a