dsp.FarrowRateConverter - Polynomial sample rate converter with arbitrary conversion factor - MATLAB (original) (raw)

Polynomial sample rate converter with arbitrary conversion factor

Description

The dsp.FarrowRateConverter System object™ implements a polynomial-fit sample rate conversion filter using a Farrow structure. You can use this object to convert the sample rate of a signal up or down by an arbitrary factor. This object supports fixed-point operations.

To convert the sample rate of a signal:

Create the dsp.FarrowRateConverter object and set its properties.
Call the object with arguments, as if it were a function.

To learn more about how System objects work, see What Are System Objects?

Creation

Syntax

Description

`frc` = dsp.FarrowRateConverter creates a polynomial filter-based sample rate converter System object, frc. For each channel of an input signal,frc converts the input sample rate to the output sample rate.

`frc` = dsp.FarrowRateConverter(`Name=Value`) sets properties using one or more name-value arguments. For example, to specify a sample rate of the input signal to 45.2 kHz, setInputSampleRate to 45200.

Example: frc = dsp.FarrowRateConverter(Specification="Coefficients",Coefficients=[1 2; 3 4]) returns a filter that converts from 44.1 kHz to 48 kHz using custom coefficients that implement a 2nd-order polynomial filter.

example

Properties

expand all

Unless otherwise indicated, properties are nontunable, which means you cannot change their values after calling the object. Objects lock when you call them, and therelease function unlocks them.

If a property is tunable, you can change its value at any time.

For more information on changing property values, seeSystem Design in MATLAB Using System Objects.

Filter Properties

Sample rate of the input signal, specified as a positive scalar in Hz. The input sample rate must be greater than the bandwidth of interest.

Sample rate of the output signal, specified as a positive scalar in Hz. The output sample rate can represent an upsample or downsample of the input signal.

Maximum tolerance for the output sample rate, specified as a positive scalar from 0 through 0.5, inclusive.

The actual output sample rate varies but is within the specified range. For example, if OutputRateTolerance is specified as 0.01, then the actual output sample rate is in the range OutputSampleRate ± 1%. This flexibility often enables a simpler filter design.

Method for specifying filter coefficients for the interpolator filter, specified as one of the following:

"Polynomial order" — Use thePolynomialOrder property to specify the order of the Lagrange-interpolation-filter polynomial. The object calculates coefficients that meet the rate and tolerance properties.
"Coefficients" — Use theCoefficients property to specify the polynomial coefficients directly.

Order of the Lagrange-interpolation-filter polynomial, specified as a positive integer less than or equal to 4. The object calculates coefficients that meet the rate and tolerance properties.

Dependencies

This property applies only when you setSpecification to "Polynomial order".

Filter polynomial coefficients, specified as a real-valued_M_-by-M matrix, where M is the polynomial order.

The diagram shows the signal flow graph for adsp.FarrowRateConverter object with coefficients set to [1 2; 3 4].

Each branch of the FIR filter corresponds to a row of the coefficient matrix.

Dependencies

This property applies only when you setSpecification to"Coefficients".

Fixed-Point Properties

Rounding method for fixed-point operations, specified as a character vector. For more information on the rounding methods see Rounding Modes.

Overflow action for fixed-point operations, specified as either"Wrap" or "Saturate". For more details on the overflow actions, see Overflow Handling.

Data type of the filter coefficients, specified as a signed numerictype (Fixed-Point Designer) object. The default data type is a signed, 16-bitnumerictype object. You must specify anumerictype object without specific binary-point scaling. To maximize precision, the object determines the fraction length of this data type based on the coefficient values.

Data type of the fractional delay, specified as an unsignednumerictype object. The default data type is an unsigned, 8-bitnumerictype object. You must specify anumerictype object without specific binary-point scaling. To maximize precision, the object determines the fraction length of this data type based on the fractional delay values.

Data type of the multiplicand, specified as a signed numerictype object. The default data type is a signed 16-bit numerictype object with 13-bit fraction length. You must specify a numerictype object that has a specific binary point scaling.

Data type of the output, specified as one of the following:

"Same word length as input" — Output word length and fraction length are the same as the input.
"Same as accumulator" — Output word length and fraction length are the same as the accumulator.
numerictype object — Signed fixed-point output data type. If you do not specify a fraction length, the object computes the fraction length based on the input range. The object preserves the dynamic range of the input.

Usage

Syntax

Description

[y](#d126e273348) = `frc`([x](#d126e273325)) resamples input x to create output y according to the rate conversion defined by frc.

example

Input Arguments

expand all

Input signal, specified as a vector or a matrix. Each column of the input is treated as a separate channel.

Output Arguments

expand all

Resampled signal, returned as a vector or matrix.

Object Functions

To use an object function, specify the System object as the first input argument. For example, to release system resources of a System object named obj, use this syntax:

expand all

freqz	Frequency response of discrete-time filter System object
freqzmr	Compute DTFT approximation of impulse response of multirate or single-rate filter
filterAnalyzer	Analyze filters with Filter Analyzer app
info	Information about filter System object
cost	Estimate cost of implementing filter System object

step	Run System object algorithm
release	Release resources and allow changes to System object property values and input characteristics
reset	Reset internal states of System object

Examples

collapse all

Note: The dsp.AudioFileWriter System object™ is not supported in MATLAB Online.

Create a dsp.FarrowRateConverter System object™ to convert an audio signal from 44.1 kHz to 96 kHz. Set the polynomial order for the filter.

FsIn = 44.1e3; FsOut = 96e3; LagrangeOrder = 2; % 1 = linear interpolation frc = dsp.FarrowRateConverter(InputSampleRate=FsIn,... OutputSampleRate=FsOut,... PolynomialOrder=LagrangeOrder); ar = dsp.AudioFileReader("guitar10min.ogg",SamplesPerFrame=14700); aw = dsp.AudioFileWriter("guitar10min_96kHz.wav",SampleRate=FsOut);

Check the resulting interpolation and decimation factors.

[interp,decim] = getRateChangeFactors(frc)

Display the polynomial that the object uses to fit the input samples.

coeffs = getPolynomialCoefficients(frc)

coeffs = 3×3

0.5000   -0.5000         0

-1.0000 0 1.0000 0.5000 0.5000 0

Convert 100 frames of the audio signal. Write the result to a file.

for n = 1:1:100 x = ar();
y = frc(x); aw(y); end

Release the dsp.AudioFileWriter System object™ to complete creation of the output file.

Plot the input and output signals. The latency of the Farrow rate converter introduces a delay in the output signal.

tx = (0:length(x)-1)./FsIn; ty = (0:length(y)-1)./FsOut;

figure

subplot(2,1,1) plot(tx,x(:,1),".") hold on plot(ty,y(:,1),"--") xlim([0 0.005]) xlabel("Time (s)") legend("Input samples","Output samples","Location","best") title("Channel 1") subplot(2,1,2) plot(tx,x(:,2),".") hold on plot(ty,y(:,2),"--") xlim([0 0.005]) xlabel("Time (s)") legend("Input samples","Output samples","Location","best") title("Channel 2")

Use the outputDelay function to determine this delay value. To account for this delay, shift the output by this delay value.

[delay,,] = outputDelay(frc,Fc=0)

tx = (0:length(x)-1)./FsIn; ty = (0:length(y)-1)./FsOut;

figure

subplot(2,1,1) plot(tx,x(:,1),".") hold on plot(ty-delay,y(:,1),"--") xlim([0 0.005]) xlabel("Time (s)") legend("Input samples","Output samples","Location","best") title("Channel 1") subplot(2,1,2) plot(tx,x(:,2),".") hold on plot(ty-delay,y(:,2),"--") xlim([0 0.005]) xlabel("Time (s)") legend("Input samples","Output samples","Location","best") title("Channel 2")

Zoom in to see the difference in sample rates.

figure subplot(2,1,1) plot(tx,x(:,1),Color=[0.6 0.6 0.6]) hold on plot(tx,x(:,1),"ro") plot(ty-delay,y(:,1),"b.") xlim([0.0105 0.0107]) legend("Interpolated input","Input samples","Output samples") title("Channel 1") subplot(2,1,2) plot(tx,x(:,2),Color=[0.6 0.6 0.6]) hold on plot(tx,x(:,2),"ro") plot(ty-delay,y(:,2),"b.") xlim([0.0105 0.0107]) legend("Interpolated input","Input samples","Output samples") title("Channel 2")

Create a dsp.FarrowRateConverter System object™ with 0% tolerance. The output rate is equal to the OutputSampleRate property. The input size must be a multiple of the decimation factor, M. In this case M is 320.

frc = dsp.FarrowRateConverter(InputSampleRate=96e3,... OutputSampleRate=44.1e3); FsOut = getActualOutputRate(frc)

[L,M] = getRateChangeFactors(frc)

Allow a 1% tolerance on the output rate and observe the difference in decimation factor.

frc.OutputRateTolerance = 0.01; FsOut2 = getActualOutputRate(frc)

[L2,M2] = getRateChangeFactors(frc)

The decimation factor is now only 13. The lower the decimation factor, the more flexibility in input size. The output rate is within the range OutputSampleRate ± 1%.

Create a dsp.FarrowRateConverter System object™ with default properties. Compute and display the frequency response.

frc = dsp.FarrowRateConverter; [h,f] = freqz(frc); plot(f,20*log10(abs(h))) ylabel("Filter Response") xlabel("Frequency (rad/s)")

Figure contains an axes object. The axes object with xlabel Frequency (rad/s), ylabel Filter Response contains an object of type line.

Create a dsp.FarrowRateConverter System object™ with default values. Determine its computational cost: the number of coefficients, number of states, multiplications per input sample, and additions per input sample.

frc = dsp.FarrowRateConverter; cst = cost(frc)

cst = struct with fields: NumCoefficients: 16 NumStates: 3 MultiplicationsPerInputSample: 13.0612 AdditionsPerInputSample: 11.9728

Repeat the computation, allowing for a 10% tolerance in the output sample rate.

frc.OutputRateTolerance = 0.1; ctl = cost(frc)

ctl = struct with fields: NumCoefficients: 16 NumStates: 3 MultiplicationsPerInputSample: 12 AdditionsPerInputSample: 11

More About

expand all

If the input is fixed point, it must be a signed integer or a signed fixed point value with a power-of-two slope and zero bias.

The diagram shows the data types that the dsp.FarrowRateConverter object uses for fixed-point signals and floating-point signals. You can specify these data types using the properties of the object, see Fixed-Point Properties. If the input is floating point, all data types in filter are the same as the input data type,single or double.

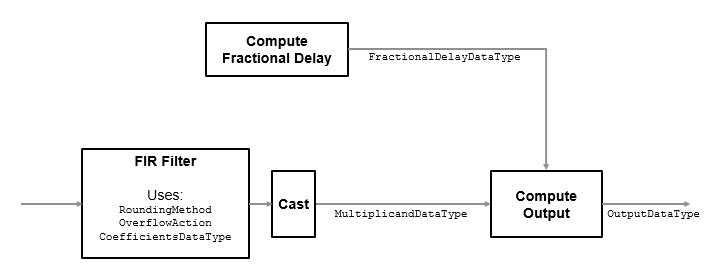
If the input is fixed point, the FIR filter defines internal data types using theRoundingMode, OverflowMode, andCoefficientsDataType properties. The accumulators and products within the FIR filter use full precision data types. The object casts the output of the FIR filter to MultiplicandDataType.

For a hardware-optimized Farrow rate converter algorithm that supports HDL code generation, use the dsphdl.FarrowRateConverter (DSP HDL Toolbox) System object. This object has hardware-friendly valid and reset control signals, and models exact hardware latency behavior. The object supports HDL code generation with HDL Coder™ tools.

Algorithms

Farrow filters implement piecewise polynomial interpolation using Horner’s rule to compute samples from the polynomial. The polynomial coefficients used to fit the input samples correspond to the Lagrange interpolation coefficients.

Once a polynomial is fitted to the input data, the value of the polynomial can be calculated at any point. Therefore, a polynomial filter enables interpolation at arbitrary locations between input samples.

You can use a polynomial of any order to fit to the existing samples. However, since large-order polynomials frequently oscillate, polynomials of order 1, 2, 3, or 4 are used in practice.

The algorithm computes interpolated values at the desired locations by varying only the fractional delay µ. This value is the interval between the previous input sample and the current output sample. All filter coefficients remain constant.

The input samples are filtered using M + 1 FIR filters, where_M_ is the polynomial order.
The outputs of these filters are multiplied by the fractional delay,µ.
The output is the sum of the multiplication results.

Here is the filter structure diagram of the Farrow filter with a polynomial order of 4.

$Input going through a sample buffer containing three delay blocks. Farrow coefficients matrix multiplied with the output of the sample buffer to form polynomial coefficients. The Horner method uses these coefficients and fractional delay to compute the output. The signals in the diagram are color coded based on their data types. Colored lines represent explicit (user-defined) data types. Input signals are color coded in blue. Farrow coefficients matrix cast is color coded in yellow and use the Coefficients data type. All the multiplicand data types are color coded in red. Fractional delay data types are color coded in green and output data type is color coded in purple. Black lines at the outputs of multipliers and adders represent implicit (derived) maximum precision data type.$

References

[1] Hentschel, T., and G. Fettweis. "Continuous-Time Digital Filters for Sample-Rate Conversion in Reconfigurable Radio Terminals." Frequenz. Vol. 55, Number 5-6, 2001, pp. 185–188.

Extended Capabilities

Version History

Introduced in R2014b

expand all

Starting in R2025a, the Filter Design HDL Coder™ product is discontinued. So, this object no longer supports HDL code generation by using the generatehdl function. For a hardware-optimized Farrow rate converter algorithm that supports HDL code generation, use the dsphdl.FarrowRateConverter (DSP HDL Toolbox) System object.