cosh - Hyperbolic cosine - MATLAB (original) (raw)

Main Content

Syntax

Description

Y = cosh([X](#d126e318171)) returns the hyperbolic cosine of the elements of X. The cosh function operates element-wise on arrays. The function accepts both real and complex inputs. All angles are in radians.

example

Examples

collapse all

Create a vector and calculate the hyperbolic cosine of each value.

X = [0 pi 2pi 3pi]; Y = cosh(X)

Y = 1×4 103 ×

0.0010    0.0116    0.2677    6.1958

Plot the hyperbolic cosine function over the domain -5≤x≤5.

x = -5:0.01:5; y = cosh(x); plot(x,y) grid on

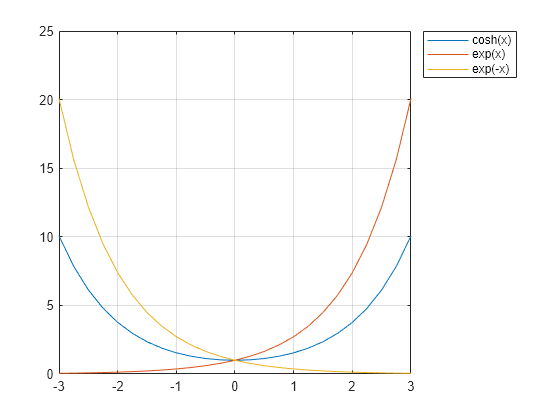
The hyperbolic cosine satisfies the identity cosh(x)=ex+e-x2. In other words, cosh(x) is the average of ex and e-x. Verify this by plotting the functions.

Create a vector of values between -3 and 3 with a step of 0.25. Calculate and plot the values of cosh(x), exp(x), and exp(-x). As expected, the curve for cosh(x) lies between the two exponential curves.

x = -3:0.25:3; y1 = cosh(x); y2 = exp(x); y3 = exp(-x); plot(x,y1,x,y2,x,y3) grid on legend('cosh(x)','exp(x)','exp(-x)','Location','bestoutside')

Input Arguments

collapse all

Input angles in radians, specified as a scalar, vector, matrix, multidimensional array, table, or timetable.

Data Types: single | double | table | timetable
Complex Number Support: Yes

More About

collapse all

The hyperbolic cosine of an angle x can be expressed in terms of exponential functions as

In terms of the traditional cosine function with a complex argument, the identity is

Extended Capabilities

expand all

Thecosh function fully supports tall arrays. For more information, see Tall Arrays.

The cosh function fully supports GPU arrays. To run the function on a GPU, specify the input data as a gpuArray (Parallel Computing Toolbox). For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).

Version History

Introduced before R2006a

expand all

The cosh function can calculate on all variables within a table or timetable without indexing to access those variables. All variables must have data types that support the calculation. For more information, see Direct Calculations on Tables and Timetables.