mean - Average or mean value of array - MATLAB (original) (raw)
Average or mean value of array
Syntax
Description
M = mean([A](#bt5b82t-1-A)) returns the mean of the elements ofA along the first array dimension whose size does not equal 1.
- If
Ais a vector, thenmean(A)returns the mean of the elements. - If
Ais a matrix, thenmean(A)returns a row vector containing the mean of each column. - If
Ais a multidimensional array, thenmean(A)operates along the first array dimension whose size does not equal 1, treating the elements as vectors. The size ofMin this dimension becomes1, while the sizes of all other dimensions remain the same as inA. - If
Ais a table or timetable, thenmean(A)returns a one-row table containing the mean of each variable. (since R2023a)
M = mean([A](#bt5b82t-1-A),`"all"`) returns the mean over all elements of A.
M = mean([A](#bt5b82t-1-A),[dim](#bt5b82t-1-dim)) returns the mean along dimension dim. For example, if A is a matrix, thenmean(A,2) returns a column vector containing the mean of each row.
M = mean([A](#bt5b82t-1-A),[vecdim](#mw%5F7e557632-72ff-44be-b891-c8646646387d)) returns the mean based on the dimensions specified in the vector vecdim. For example, ifA is a matrix, then mean(A,[1 2]) returns the mean of all elements in A because every element of a matrix is contained in the array slice defined by dimensions 1 and 2.
M = mean(___,[outtype](#bt5b82t-1-outtype)) returns the mean with a specified data type for any of the previous syntaxes. outtype can be"default", "double", or "native".
M = mean(___,[missingflag](#mw%5F44035159-4a67-4049-b7c3-b6903c5de7a7)) specifies whether to include or omit missing values in A. For example,mean(A,"omitmissing") ignores all missing values when computing the mean. By default, mean includes missing values.
M = mean(___,Weights=[W](#mw%5F2ccfc7be-2982-4dd2-88f6-5bd187b4fc88)) specifies a weighting scheme W and returns the weighted mean. (since R2024a)
Examples
Mean of Matrix Columns
Create a matrix and compute the mean of each column.
A = [0 1 1; 2 3 2; 1 3 2; 4 2 2]
A = 4×3
0 1 1
2 3 2
1 3 2
4 2 2M = 1×3
1.7500 2.2500 1.7500Mean of Matrix Rows
Create a matrix and compute the mean of each row.
A = [0 1 1; 2 3 2; 3 0 1; 1 2 3]
A = 4×3
0 1 1
2 3 2
3 0 1
1 2 3M = 4×1
0.6667
2.3333
1.3333
2.0000Mean of 3-D Array
Create a 4-by-2-by-3 array of integers between 1 and 10 and compute the mean values along the second dimension.
rng('default') A = randi(10,[4,2,3]); M = mean(A,2)
M = M(:,:,1) =
8.0000
5.5000
2.5000
8.0000M(:,:,2) =
10.0000 7.5000 5.5000 6.0000
M(:,:,3) =
6.0000
5.5000
8.500010.0000
Mean of Array Page
Create a 3-D array and compute the mean over each page of data (rows and columns).
A(:,:,1) = [2 4; -2 1]; A(:,:,2) = [9 13; -5 7]; A(:,:,3) = [4 4; 8 -3]; M1 = mean(A,[1 2])
M1 = M1(:,:,1) =
1.2500M1(:,:,2) =
6M1(:,:,3) =
3.2500To compute the mean over all dimensions of an array, you can either specify each dimension in the vector dimension argument, or use the "all" option.
Mean of Single-Precision Array
Create a single-precision vector of ones and compute its single-precision mean.
A = single(ones(10,1)); M = mean(A,"native")
The result is also in single precision.
Mean Excluding Missing Values
Create a matrix containing NaN values.
A = [1.77 -0.005 NaN -2.95; NaN 0.34 NaN 0.19]
A = 2×4
1.7700 -0.0050 NaN -2.9500
NaN 0.3400 NaN 0.1900Compute the mean values of the matrix, excluding missing values. For matrix columns that contain any NaN value, mean computes with the non-NaN elements. For matrix columns that contain all NaN values, the mean is NaN.
M = 1×4
1.7700 0.1675 NaN -1.3800Weighted Mean
Since R2024a
Create a matrix and compute the weighted mean of the matrix according to a weighting scheme specified by W. The mean function applies the weighting scheme to each column in A.
A = [1 1; 7 9; 1 9; 1 9; 6 2]; W = [1 2 1 2 3]'; M = mean(A,Weights=W)
Input Arguments
A — Input data
vector | matrix | multidimensional array | table | timetable
Input data, specified as a vector, matrix, multidimensional array, table, or timetable.
- If
Ais a scalar, thenmean(A)returnsA. - If
Ais an empty 0-by-0 matrix, thenmean(A)returnsNaN.
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | logical | datetime | duration | table | timetable
dim — Dimension to operate along
positive integer scalar
Dimension to operate along, specified as a positive integer scalar. If you do not specify the dimension, then the default is the first array dimension whose size does not equal 1.
Dimension dim indicates the dimension whose length reduces to 1. The size(M,dim) is 1, while the sizes of all other dimensions remain the same.
Consider an m-by-n input matrix,A:
mean(A,1)computes the mean of the elements in each column ofAand returns a1-by-nrow vector.
mean(A,2)computes the mean of the elements in each row ofAand returns anm-by-1column vector.
mean returns A when dim is greater than ndims(A) or when size(A,dim) is 1.
vecdim — Vector of dimensions
vector of positive integers
Vector of dimensions, specified as a vector of positive integers. Each element represents a dimension of the input data. The lengths of the output in the specified operating dimensions are 1, while the others remain the same.
Consider a 2-by-3-by-3 input data, A. Then mean(A,[1 2]) returns a 1-by-1-by-3 array whose elements are the means over each page ofA.
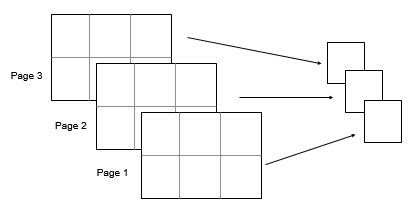
outtype — Output data type
"default" (default) | "double" | "native"
Output data type, specified as one of the values in this table. These options also specify the data type in which the operation is performed.
| outtype | Output data type |
|---|---|
| "default" | double, unless the input data type is single,duration,datetime, table, ortimetable, in which case, the output is "native" |
| "double" | double, unless the data input type is duration,datetime, table, or timetable, in which case,"double" is not supported |
| "native" | Same data type as the input, unless:Input data type is logical, in which case, the output isdoubleInput data type is char, in which case, "native" is not supportedInput data type istimetable, in which case, the output is table |
missingflag — Missing value condition
"includemissing" (default) | "includenan" | "includenat" | "omitmissing" | "omitnan" | "omitnat"
Missing value condition, specified as one of the values in this table.
| Value | Input Data Type | Description |
|---|---|---|
| "includemissing" | All supported data types | Include missing values inA when computing the mean. If any element in the operating dimension is missing, then the corresponding element in M is missing. |
| "includenan" | double, single,duration | |
| "includenat" | datetime | |
| "omitmissing" | All supported data types | Ignore missing values inA, and compute the mean over fewer points. If all elements in the operating dimension are missing, then the corresponding element inM is missing. |
| "omitnan" | double, single,duration | |
| "omitnat" | datetime |
W — Weighting scheme
vector | matrix | multidimensional array
Since R2024a
Weighting scheme, specified as a vector, matrix, or multidimensional array. The elements ofW must be nonnegative.
If you specify a weighting scheme, mean returns the weighted mean, which is useful when values in the input data have different levels of importance or the input data is skewed.
If W is a vector, it must have the same length as the operating dimension. Otherwise, W must have the same size as the input data.
If the input data A is a table or timetable, thenW must be a vector.
You cannot specify this argument if you specify vecdim or"all".
Data Types: double | single
More About
Mean
For a finite-length vector A made up of_N_ scalar observations, the mean is defined as
Weighted Mean
For a finite-length vector A made up of_N_ scalar observations and weighting scheme_W_, the weighted mean is defined as
μW=∑i=1NWiAi∑i=1NWi.
Extended Capabilities
Tall Arrays
Calculate with arrays that have more rows than fit in memory.
Themean function supports tall arrays with the following usage notes and limitations:
- The
Weightsname-value argument is not supported.
For more information, see Tall Arrays.
C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.
Usage notes and limitations:
- If you specify
dim, then it must be a constant. - The
outtypeandmissingflagoptions must be constant character vectors or strings. - Integer types do not support the
"native"output data type option. - See Variable-Sizing Restrictions for Code Generation of Toolbox Functions (MATLAB Coder).
GPU Code Generation
Generate CUDA® code for NVIDIA® GPUs using GPU Coder™.
Usage notes and limitations:
- If you specify
dim, then it must be a constant. - The
outtypeandmissingflagoptions must be constant character vectors or strings. - Integer types do not support the
"native"output data type option. - The
Weightsname-value argument is not supported.
Thread-Based Environment
Run code in the background using MATLAB® backgroundPool or accelerate code with Parallel Computing Toolbox™ ThreadPool.
This function fully supports thread-based environments. For more information, see Run MATLAB Functions in Thread-Based Environment.
GPU Arrays
Accelerate code by running on a graphics processing unit (GPU) using Parallel Computing Toolbox™.
The mean function supports GPU array input with these usage notes and limitations:
- The
"native"option is not supported.
For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).
Distributed Arrays
Partition large arrays across the combined memory of your cluster using Parallel Computing Toolbox™.
Usage notes and limitations:
- The
"native"option is not supported.
For more information, see Run MATLAB Functions with Distributed Arrays (Parallel Computing Toolbox).
Version History
Introduced before R2006a
R2024b: Compute weighted mean for datetime data type
You can compute the weighted mean for input data having thedatetime data type. Before R2024b, you could compute only the unweighted mean for this data type.
R2024a: Compute weighted mean
Compute the weighted mean by specifying the Weights parameter as the weighting scheme. You can compute the weighted mean for input data having numeric, logical, and duration data types.
R2023a: Perform calculations directly on tables and timetables
The mean function can calculate on all variables within a table or timetable without indexing to access those variables. All variables must have data types that support the calculation. For more information, see Direct Calculations on Tables and Timetables.
R2023a: Specify missing value condition
Include or omit all missing values in the input data when computing the mean by using the"includemissing" or "omitmissing" options. Previously,"includenan", "omitnan", "includenat", and"omitnat" specified a missing value condition that was specific to the data type of the input data.
R2023a: Improved performance with small group size
The mean function shows improved performance when computing over a real vector when the operating dimension is not specified. The function determines the default operating dimension more quickly in R2023a than in R2022b.
For example, this code computes the mean along the default vector dimension. The code is about 2.2x faster than in the previous release.
function timingMean A = rand(10,1); for i = 1:8e5 mean(A); end end
The approximate execution times are:
R2022b: 0.91 s
R2023a: 0.41 s
The code was timed on a Windows® 10, Intel® Xeon® CPU E5-1650 v4 @ 3.60 GHz test system using thetimeit function.
R2018b: Operate on multiple dimensions
Operate on multiple dimensions of the input data at a time. Specify a vector of operating dimensions, or specify the "all" option to operate on all array dimensions.