sin - Sine of argument in radians - MATLAB (original) (raw)

Main Content

Sine of argument in radians

Syntax

Description

[Y](#bt5p3vk-1-Y) = sin([X](#bt5p3vk-1-X)) returns the sine of the elements of X. The sin function operates element-wise on arrays. The function accepts both real and complex inputs.

• For real values of X, sin(X) returns real values in the interval [-1, 1].
• For complex values of X,sin(X) returns complex values.

example

Examples

collapse all

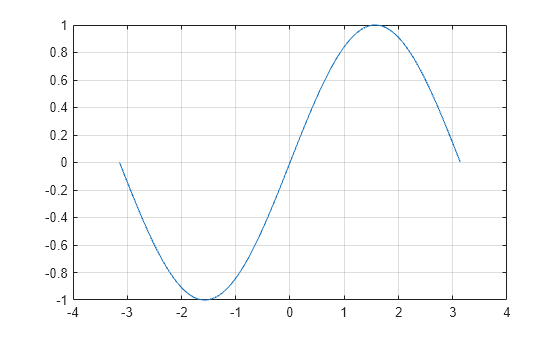
Plot Sine Function

Plot the sine function over the domain -π≤x≤π.

x = -pi:0.01:pi; plot(x,sin(x)), grid on

Sine of Vector of Complex Angles

Calculate the sine of the complex angles in vector x.

x = [-i pi+ipi/2 -1+i4]; y = sin(x)

y = 1×3 complex

0.0000 - 1.1752i 0.0000 - 2.3013i -22.9791 +14.7448i

Input Arguments

collapse all

X — Input angle in radians

scalar | vector | matrix | multidimensional array | table | timetable

Input angle in radians, specified as a scalar, vector, matrix, multidimensional array, table, or timetable.

Data Types: single | double | table | timetable
Complex Number Support: Yes

Output Arguments

collapse all

Y — Sine of input angle

scalar | vector | matrix | multidimensional array | table | timetable

Sine of input angle, returned as a real-valued or complex-valued scalar, vector, matrix, multidimensional array, table, or timetable.

More About

collapse all

Sine Function

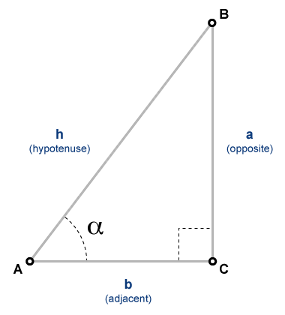
The sine of an angle, α, defined with reference to a right triangle is

sin(α)=opposite sidehypotenuse=ah .

The sine of a complex argument, α, is

Tips

• To compute sin(X*pi) accurately, without usingpi as a floating-point approximation of π, you can use the sinpi function instead. For example, sinpi(n) is exactly zero for integers n andsinpi(m/2) is +1 or –1 for odd integersm.

Extended Capabilities

Tall Arrays

Calculate with arrays that have more rows than fit in memory.

Thesin function fully supports tall arrays. For more information, see Tall Arrays.

C/C++ Code Generation

Generate C and C++ code using MATLAB® Coder™.

GPU Code Generation

Generate CUDA® code for NVIDIA® GPUs using GPU Coder™.

Thread-Based Environment

Run code in the background using MATLAB® backgroundPool or accelerate code with Parallel Computing Toolbox™ ThreadPool.

GPU Arrays

Accelerate code by running on a graphics processing unit (GPU) using Parallel Computing Toolbox™.

The sin function fully supports GPU arrays. To run the function on a GPU, specify the input data as a gpuArray (Parallel Computing Toolbox). For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).

Distributed Arrays

Partition large arrays across the combined memory of your cluster using Parallel Computing Toolbox™.

Version History

Introduced before R2006a

expand all

R2023a: Perform calculations directly on tables and timetables

The sin function can calculate on all variables within a table or timetable without indexing to access those variables. All variables must have data types that support the calculation. For more information, see Direct Calculations on Tables and Timetables.