var - Variance - MATLAB (original) (raw)

Syntax

Description

[V](#mw%5F574ac288-b828-4cd6-830a-85d986cf97bb) = var([A](#bum7s4o-1-A)) returns the variance of the elements of A along the first array dimension whose size does not equal 1. By default, the variance is normalized by N-1, where N is the number of observations.

• If A is a vector of observations, thenV is a scalar.
• If A is a matrix whose columns are random variables and whose rows are observations, then V is a row vector containing the variance corresponding to each column.
• If A is a multidimensional array, thenvar(A) operates along the first array dimension whose size does not equal 1, treating the elements as vectors. The size ofV in this dimension becomes 1, while the sizes of all other dimensions are the same as inA.
• If A is a scalar, then V is0.
• If A is a 0-by-0 empty array, then V is NaN.
• If A is a table or timetable, then var(A) returns a one-row table containing the variance of each variable. (since R2023a)

example

[V](#mw%5F574ac288-b828-4cd6-830a-85d986cf97bb) = var([A](#bum7s4o-1-A),[w](#bum7s4o-1-w)) specifies a weighting scheme. When w = 0 (default), the variance is normalized by N-1, where N is the number of observations. When w = 1, the variance is normalized by the number of observations. w can also be a weight vector containing nonnegative elements. In this case, the length of w must equal the length of the dimension over which var is operating.

example

[V](#mw%5F574ac288-b828-4cd6-830a-85d986cf97bb) = var([A](#bum7s4o-1-A),[w](#bum7s4o-1-w),`"all"`) returns the variance over all elements of A whenw is either 0 or 1.

[V](#mw%5F574ac288-b828-4cd6-830a-85d986cf97bb) = var([A](#bum7s4o-1-A),[w](#bum7s4o-1-w),[dim](#bum7s4o-1-dim)) returns the variance along dimension dim. To maintain the default normalization while specifying the dimension of operation, set w = 0 in the second argument.

example

[V](#mw%5F574ac288-b828-4cd6-830a-85d986cf97bb) = var([A](#bum7s4o-1-A),[w](#bum7s4o-1-w),[vecdim](#mw%5F97b9faf9-0e60-4e8e-9ac8-47f926514dea)) returns the variance over the dimensions specified in the vectorvecdim when w is 0 or 1. For example, ifA is a matrix, then var(A,0,[1 2]) returns the variance over all elements in A because every element of a matrix is contained in the array slice defined by dimensions 1 and 2.

example

[V](#mw%5F574ac288-b828-4cd6-830a-85d986cf97bb) = var(___,[nanflag](#mw%5Fa045058e-a680-46d9-a03c-80ec7e139dc7)) specifies whether to include or omit NaN values inA for any of the previous syntaxes. For example,var(A,"omitnan") ignores NaN values when computing the variance. By default, var includesNaN values.

example

Examples

collapse all

Create a matrix and compute its variance.

A = [4 -7 3; 1 4 -2; 10 7 9]; var(A)

ans = 1×3

21.0000 54.3333 30.3333

Create a 3-D array and compute its variance.

A(:,:,1) = [1 3; 8 4]; A(:,:,2) = [3 -4; 1 2]; var(A)

ans = ans(:,:,1) =

24.5000 0.5000

ans(:,:,2) =

 2    18

Create a matrix and compute its variance according to a weight vector w.

A = [5 -4 6; 2 3 9; -1 1 2]; w = [0.5 0.25 0.25]; var(A,w)

ans = 1×3

6.1875    9.5000    6.1875

Create a matrix and compute its variance along the first dimension.

A = [4 -2 1; 9 5 7]; var(A,0,1)

ans = 1×3

12.5000 24.5000 18.0000

Compute the variance of A along the second dimension.

Create a 3-D array and compute the variance over each page of data (rows and columns).

A(:,:,1) = [2 4; -2 1]; A(:,:,2) = [9 13; -5 7]; A(:,:,3) = [4 4; 8 -3]; V = var(A,0,[1 2])

V = V(:,:,1) =

6.2500

V(:,:,2) =

60

V(:,:,3) =

20.9167

Create a matrix containing NaN values.

A = [1.77 -0.005 NaN -2.95; NaN 0.34 NaN 0.19]

A = 2×4

1.7700   -0.0050       NaN   -2.9500
   NaN    0.3400       NaN    0.1900

Compute the variance of the matrix, excluding NaN values. For matrix columns that contain any NaN value, var computes with non-NaN elements. For matrix columns that contain all NaN values, the variance is NaN.

V = 1×4

     0    0.0595       NaN    4.9298

Create a matrix and compute the variance and mean of each column.

A = [4 -7 3; 1 4 -2; 10 7 9]; [V,M] = var(A)

V = 1×3

21.0000 54.3333 30.3333

M = 1×3

5.0000    1.3333    3.3333

Create a matrix and compute the weighted variance and weighted mean of each column according to a weight vector w.

A = [5 -4 6; 2 3 9; -1 1 2]; w = [0.5 0.25 0.25]; [V,M] = var(A,w)

V = 1×3

6.1875    9.5000    6.1875

M = 1×3

2.7500   -1.0000    5.7500

Input Arguments

collapse all

Input array, specified as a vector, matrix, multidimensional array, table, or timetable. IfA is a scalar, then var(A) returns0. If A is a0-by-0 empty array, thenvar(A) returns NaN.

Data Types: single | double | table | timetable
Complex Number Support: Yes

Weight, specified as one of:

• 0 — Normalize byN-1, where N is the number of observations. If there is only one observation, then the weight is 1.
• 1 — Normalize byN.
• Vector made up of nonnegative scalar weights corresponding to the dimension of A along which the variance is calculated.

Data Types: single | double

Dimension to operate along, specified as a positive integer scalar. If you do not specify the dimension, then the default is the first array dimension whose size does not equal 1.

Dimension dim indicates the dimension whose length reduces to 1. The size(V,dim) is 1, while the sizes of all other dimensions remain the same.

Consider an m-by-n input matrix,A:

• var(A,0,1) computes the variance of the elements in each column of A and returns a1-by-n row vector.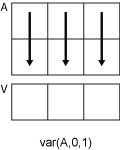
  
• var(A,0,2) computes the variance of the elements in each row of A and returns anm-by-1 column vector.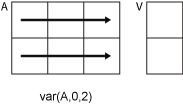
  

If dim is greater than ndims(A), then var(A) returns an array of zeros the same size asA.

Vector of dimensions, specified as a vector of positive integers. Each element represents a dimension of the input array. The lengths of the output in the specified operating dimensions are 1, while the others remain the same.

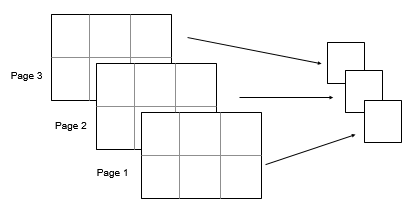
Consider a 2-by-3-by-3 input array, A. Thenvar(A,0,[1 2]) returns a 1-by-1-by-3 array whose elements are the variances computed over each page ofA.

Missing value condition, specified as one of these values:

• "includemissing" or"includenan" — IncludeNaN values in A when computing the variance. If any element in the operating dimension isNaN, then the corresponding element inV is NaN."includemissing" and"includenan" have the same behavior.
• "omitmissing" or "omitnan" — Ignore NaN values inA and w, and compute the variance over fewer points. If all elements in the operating dimension are NaN, then the corresponding element in V is NaN."omitmissing" and"omitnan" have the same behavior.

Output Arguments

collapse all

Variance, returned as a scalar, vector, matrix, multidimensional array, or table.

• If A is a vector of observations, thenV is a scalar.
• If A is a matrix whose columns are random variables and whose rows are observations, thenV is a row vector containing the variance corresponding to each column.
• If A is a multidimensional array, thenvar(A) operates along the first array dimension whose size does not equal 1, treating the elements as vectors. The size of V in this dimension becomes 1, while the sizes of all other dimensions are the same as in A.
• If A is a scalar, then V is 0.
• If A is a0-by-0 empty array, then V is NaN.
• If A is a table or timetable, then V is a one-row table. If the variables of A have units, then the variables of V do not have those units. (since R2023a)

Mean, returned as a scalar, vector, matrix, multidimensional array, or table.

• If A is a vector of observations, thenM is a scalar.
• If A is a matrix whose columns are random variables and whose rows are observations, thenM is a row vector containing the mean corresponding to each column.
• If A is a multidimensional array, thenvar(A) operates along the first array dimension whose size does not equal 1, treating the elements as vectors. The size of M in this dimension becomes 1, while the sizes of all other dimensions are the same as in A.
• If A is a scalar, then M is equal to A.
• If A is a0-by-0 empty array, then M is NaN.
• If A is a table or timetable, then M is a one-row table. If the variables of A have units, then the variables of M have the same units. (since R2023a)

If V is the weighted variance, thenM is the weighted mean.

More About

collapse all

For a random variable vector A made up of_N_ scalar observations, the variance is defined as

where μ is the mean of A,

Some definitions of variance use a normalization factor_N_ instead of N – 1. You can use a normalization factor of N by specifying a weight of1, producing the second moment of the sample about its mean.

Regardless of the normalization factor for the variance, the mean is assumed to have the normalization factor N.

For a finite-length vector A made up of_N_ scalar observations and weighting schemew, the weighted variance is defined as

where μw is the weighted mean of A.

For a finite-length vector A made up of_N_ scalar observations and weighting schemew, the weighted mean is defined as

Extended Capabilities

expand all

Usage notes and limitations:

• Code generation does not support the output argumentM.
• If used, the arguments dim,vecdim, and nanflag must be constant at code generation time.
• For input argument A:
  • If you do not specify a dimension, the code generator operates along the first dimension of the input array that is variable size or whose size does not equal 1. If this dimension is variable size at code generation time and is 1 at run time, a run-time error can occur. To avoid this error, specify the dimension.
  • If all dimensions of the input array are variable size at code generation time, this array cannot be empty at run time.

Usage notes and limitations:

• If specified, dim must be a constant.
• GPU code generation supports the following syntaxes:
  • V = var(A)
  • V = var(A,w)
  • V = var(A,w,"all")
  • V = var(A,w,dim)
  • V = var(A,w,vecdim)
  • V = var(__,nanflag)

The var function fully supports GPU arrays. To run the function on a GPU, specify the input data as a gpuArray (Parallel Computing Toolbox). For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).

Version History

Introduced before R2006a

expand all

The var function can calculate on all variables within a table or timetable without indexing to access those variables. All variables must have data types that support the calculation. For more information, see Direct Calculations on Tables and Timetables.

Include or omit missing values in the input arrays when computing the variance by using the "includemissing" or "omitmissing" options. These options have the same behavior as the "includenan" and "omitnan" options, respectively.

The var function shows improved performance when computing over a real vector when the operating dimension is not specified. The function determines the default operating dimension more quickly in R2023a than in R2022b.

For example, this code computes the variance along the default vector dimension. The code is about 1.6x faster than in the previous release.

function timingVar A = rand(10,1); for i = 1:8e5 var(A); end end

The approximate execution times are:

R2022b: 1.29 s

R2023a: 0.79 s

The code was timed on a Windows® 10, Intel® Xeon® CPU E5-1650 v4 @ 3.60 GHz test system using thetimeit function.

The var function can now return the mean of the input elements used to calculate the variance by using a second output argumentM. If a weighting scheme is specified, thenvar returns the weighted mean.

Operate on multiple dimensions of the input array at a time. Specify a vector of operating dimensions, or specify the "all" option to operate on all array dimensions.