meshgrid - 2-D and 3-D grids - MATLAB (original) (raw)
Syntax
Description
[[X](#bvblp7l-X),[Y](#bvblp7l-Y)] = meshgrid([x](#bvblp7l-x),[y](#bvblp7l-y)) returns 2-D grid coordinates based on the coordinates contained in vectors x and y. X is a matrix where each row is a copy of x, and Y is a matrix where each column is a copy of y. The grid represented by the coordinates X and Y has length(y) rows and length(x) columns.
[[X](#bvblp7l-X),[Y](#bvblp7l-Y)] = meshgrid([x](#bvblp7l-x)) is the same as [X,Y] = meshgrid(x,x), returning square grid coordinates with grid size length(x)-by-length(x).
[[X](#bvblp7l-X),[Y](#bvblp7l-Y),[Z](#bvblp7l-Z)] = meshgrid([x](#bvblp7l-x),[y](#bvblp7l-y),[z](#bvblp7l-z)) returns 3-D grid coordinates defined by the vectors x, y, and z. The grid represented by X, Y, and Z has size length(y)-by-length(x)-by-length(z).
[[X](#bvblp7l-X),[Y](#bvblp7l-Y),[Z](#bvblp7l-Z)] = meshgrid([x](#bvblp7l-x)) is the same as [X,Y,Z] = meshgrid(x,x,x), returning 3-D grid coordinates with grid size length(x)-by-length(x)-by-length(x).
Examples
2-D Grid
Create 2-D grid coordinates with _x_-coordinates defined by the vector x and _y_-coordinates defined by the vector y.
x = 1:3; y = 1:5; [X,Y] = meshgrid(x,y)
X = 5×3
1 2 3
1 2 3
1 2 3
1 2 3
1 2 3Y = 5×3
1 1 1
2 2 2
3 3 3
4 4 4
5 5 5Evaluate the expression x2+y2 over the 2-D grid.
ans = 5×3
2 5 10
5 8 13
10 13 18
17 20 25
26 29 34Plot Surface
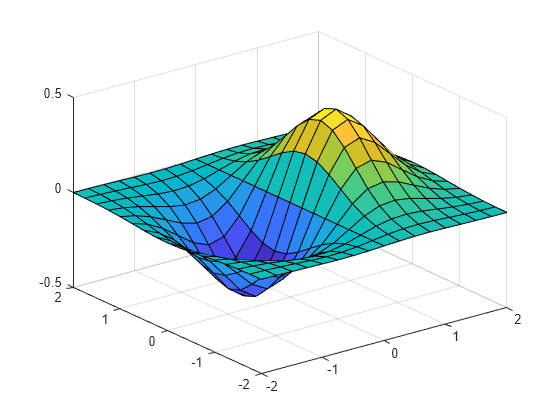
Create a 2-D grid with uniformly spaced _x_-coordinates and _y_-coordinates in the interval [-2,2].
x = -2:0.25:2; y = x; [X,Y] = meshgrid(x);
Evaluate and plot the function f(x,y)=xe-x2-y2 over the 2-D grid.
F = X.*exp(-X.^2-Y.^2); surf(X,Y,F)
Starting in R2016b, it is not always necessary to create the grid before operating over it. For example, computing the expression xe-x2-y2 implicitly expands the vectors x and y. For more information on implicit expansion, see Array vs. Matrix Operations.
surf(x,y,x.*exp(-x.^2-(y').^2))

3-D Grid
Create 3-D grid coordinates from _x_-, _y_-, and _z_-coordinates defined in the interval [0,6], and evaluate the expression x2+y2+z2.
x = 0:2:6; y = 0:1:6; z = 0:3:6; [X,Y,Z] = meshgrid(x,y,z); F = X.^2 + Y.^2 + Z.^2;
Determine the size of the grid. The three coordinate vectors have different lengths, forming a rectangular box of grid points.
Use the single-input syntax to generate a uniformly spaced 3-D grid based on the coordinates defined in x. The new grid forms a cube of grid points.
[X,Y,Z] = meshgrid(x); G = X.^2 + Y.^2 + Z.^2; gridsize = size(G)
Input Arguments
x — x-coordinates of points
vector
x-coordinates of points, specified as a vector.
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
y — y-coordinates of points
vector
y-coordinates of points, specified as a vector.
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
z — z-coordinates of points
vector
z-coordinates of points, specified as a vector.
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
Output Arguments
X — x-coordinates over grid
2-D or 3-D array
x-coordinates over a grid, returned as a 2-D (two inputs) or 3-D array (three inputs).
Y — y-coordinates over grid
2-D or 3-D array
y-coordinates over a grid, returned as a 2-D (two inputs) or 3-D array (three inputs).
Z — z-coordinates over grid
3-D array
z-coordinates over a grid, returned as a 3-D array.
More About
Convert Between meshgrid and ndgrid Formats
meshgrid and ndgrid create grids using different output formats. Specifically, the first two dimensions of a grid created using one of these functions are swapped when compared to the other grid format. Some MATLAB® functions use grids in meshgrid format, while others usendgrid format, so it is common to convert grids between the two formats.
You can convert between these grid formats using pagetranspose (as of R2020b) or permute to swap the first two dimensions of the grid arrays. For example, create a 3-D grid with meshgrid.
[X,Y,Z] = meshgrid(1:4,1:3,1:2);
Now transpose the first two dimensions of each grid array to convert the grid to ndgrid format, and compare the results against the outputs from ndgrid.
Xt = pagetranspose(X); Yt = pagetranspose(Y); Zt = pagetranspose(Z); [Xn,Yn,Zn] = ndgrid(1:4,1:3,1:2); isequal(Xt,Xn) & isequal(Yt,Yn) & isequal(Zt,Zn)
Using pagetranspose is equivalent to permuting the first two dimensions while leaving other dimensions the same. You can also perform this operation using permute(X,[2 1 3:ndims(X)]).
Extended Capabilities
C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.
GPU Code Generation
Generate CUDA® code for NVIDIA® GPUs using GPU Coder™.
Thread-Based Environment
Run code in the background using MATLAB® backgroundPool or accelerate code with Parallel Computing Toolbox™ ThreadPool.
This function fully supports thread-based environments. For more information, see Run MATLAB Functions in Thread-Based Environment.
GPU Arrays
Accelerate code by running on a graphics processing unit (GPU) using Parallel Computing Toolbox™.
The meshgrid function supports GPU array input with these usage notes and limitations:
- The inputs must be floating-point double or single.
For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).
Distributed Arrays
Partition large arrays across the combined memory of your cluster using Parallel Computing Toolbox™.
Usage notes and limitations:
- The inputs must be floating-point double or single.
For more information, see Run MATLAB Functions with Distributed Arrays (Parallel Computing Toolbox).
Version History
Introduced before R2006a