stabilization of lasers (original) (raw)
Definition: measures applied to lasers to improve their stability in terms of output power, optical frequency, or other quantities
Categories:  laser devices and laser physics,
laser devices and laser physics,  fluctuations and noise,
fluctuations and noise,  methods
methods
Related: frequency-stabilized laserslaser noiseintensity noisespikingphase noiselinewidthnoise eaterslasersinjection lockingcarrier–envelope offsetfrequency combsfrequency metrology
Page views in 12 months: 3248
DOI: 10.61835/fkd Cite the article: BibTex BibLaTex plain textHTML Link to this page! LinkedIn
Content quality and neutrality are maintained according to our editorial policy.
📦 For purchasing laser stabilization, use the RP Photonics Buyer's Guide — an expert-curated directory for finding all relevant suppliers, which also offers advanced purchasing assistance.
Contents
Introduction
As lasers exhibit various kinds of laser noise, which can be detrimental in applications, it is sometimes necessary to use techniques for suppressing noise and stabilizing certain laser parameters. There are active and passive stabilization schemes, as discussed in the following. Concerning frequency stabilization, see the article on frequency-stabilized lasers for more details.
See also the article on synchronization of lasers, which treats both timing and phase synchronization.
Active Laser Stabilization
Active stabilization schemes usually involve some kind of electronic feedback (or sometimes feedforward) system, where fluctuations in some parameters are converted to an electronic signal, which is then used to act on the laser in some way.
Examples are:
- The output power of a laser may be stabilized with a scheme as shown in Figure 1. The laser power is monitored with a photodiode and corrected e.g. via control of the pump power or the losses in or outside the laser resonator. In this way, both spiking after turn-on and the intensity noise under steady-state conditions can be reduced.
- Note that it is also possible to reduce intensity noise by acting on the output beam instead of the laser itself; see the article on noise eaters.

Figure 1: Diode-pumped solid-state laser with a feedback system stabilizing the output power.
- The optical frequency of a single-frequency laser, or the frequency of one line of the frequency comb from a mode-locked laser, can be stabilized via resonator length control. The feedback signal can be obtained e.g. by recording a beat note with a second laser, by measuring the power which is transmitted or reflected at a very stable reference cavity or another kind of interferometer, or by measuring the transmission of a gas cell (e.g. an iodine cell), possibly using Doppler-free laser absorption spectroscopy. A frequently used technique for generating an error signal with a reference cavity is the Pound–Drever–Hall method [3, 4], using a weak phase modulation of the light which is sent to the reference cavity. A scheme not requiring such modulation is the Hänsch–Couillaud method [2]. Another method is tilt locking, where spatial mode interference is utilized [12, 16, 30]. (See the article on frequency-stabilized lasers.)
- The stabilization of the carrier–envelope offset phase or frequency of a mode-locked laser (CEO stabilization) can be based on, e.g., a phase measurement with an ($f-2f$) interferometer and feedback via some wedge or tilted mirror in the laser resonator. This kind of stabilization is important for frequency metrology.
- The timing of the pulses (→ timing jitter) from a mode-locked laser can be monitored by comparing the phases of a photodiode signal and of an electronic reference oscillator, and stabilized e.g. via cavity length control.
- Stabilization of the pointing direction of the output beam is possible via a beam position measurement (e.g. with a four-quadrant photodiode) and correction via piezo-controlled resonator mirrors.
The stability which is achieved with such active systems is determined by factors such as photodetection noise, the bandwidth of control elements, the design of the feedback electronics, and the stability of the reference standards (e.g. optical reference cavities).
Passive Laser Stabilization
Passive schemes do not involve electronics and are based on purely optical effects. Examples are:
- The frequency of a laser can be stabilized via optical feedback from a stable reference cavity. (This may also be considered as using an extended laser resonator, being a kind of composite cavity.)
- Synchronization of two mode-locked lasers is possible via cross-phase modulation in a Kerr medium, in which the intracavity pulses of both lasers meet.
- One may also employ nonlinear optical effects such as frequency doubling, which causes higher losses for higher powers [33].
The optical frequency of a laser may also be stabilized by injection locking, i.e., injecting a beam with a highly stable optical frequency from another laser.
Frequently Asked Questions
This FAQ section was generated with AI based on the article content and has been reviewed by the article’s author (RP).
What is the difference between active and passive laser stabilization?
Active stabilization schemes use an electronic feedback system to measure fluctuations in a laser parameter and actively correct them. Passive schemes are based on purely optical effects and do not involve electronics.
How can the output power of a laser be stabilized?
Laser output power can be actively stabilized by monitoring it with a photodiode and using the signal in a feedback loop to control the pump power or the losses within or outside the laser resonator.
Which laser parameters are commonly stabilized?
How can a laser's optical frequency be stabilized?
A laser's frequency can be stabilized by locking it to a highly stable reference, such as an optical reference cavity or a gas cell. An electronic feedback system then typically adjusts the laser's resonator length to correct for frequency drift.
Suppliers
Sponsored content: The RP Photonics Buyer's Guide contains 18 suppliers for laser stabilization. Among them:
⚙ hardware
Menlo Systems offers ultrastable, frequency stabilized lasers at basically any wavelength. We supply fully characterized systems with linewidths < 1 Hz and Allan deviations of 2 × 10−15 (in 1 s) as well as modules and components allowing for state-of-the-art systems tailored to your requirements.
⚙ hardware
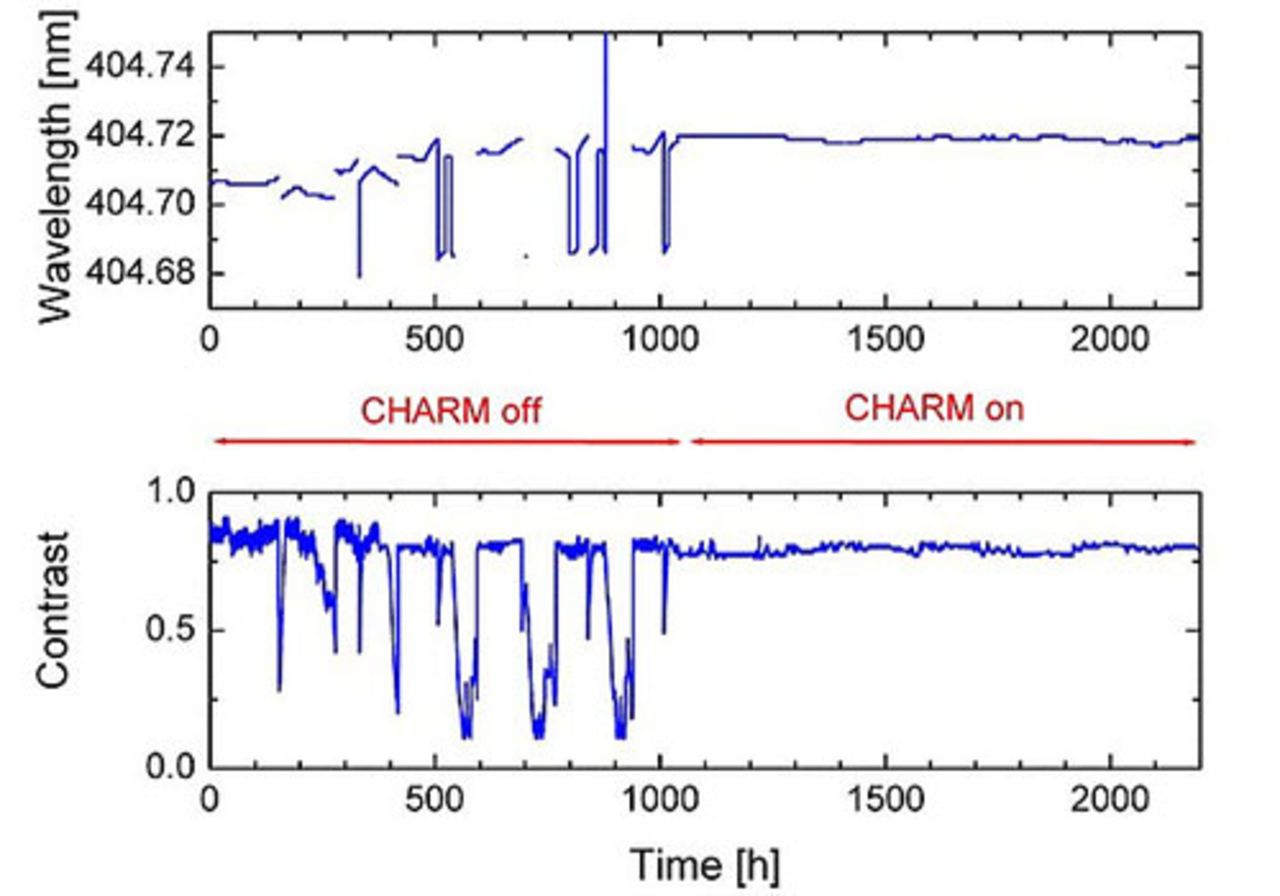
TOPTICA’s unique CHARM technology (Coherence-advanced regulation method) provides an active stabilization of the laser’s coherence. An integral feature of the TopMode laser family, this scheme ensures excellent long-term stability of the lasing wavelength and output power, as well as an extremely low intensity noise.
⚙ hardware
The SLICE-OPL tightly locks frequencies from as low as 10 MHz up to > 9.3 GHz, making it well-suited for stabilizing frequency combs. A built-in touchscreen GUI allows the user to manipulate the error signal and engage the lock — all without an oscilloscope.
Ideal for precision spectroscopy and metrology applications, the SLICE-DLC Dual Laser Controller is an ultra-low-noise, two-channel current source, each channel with two temperature controls for sub-millikelvin diode stability to minimize frequency fluctuations and drift. A current servo input gives high-speed (≥10 MHz) control of the laser.
The D2-125 Laser Servo with Lock Guard auto-relocking enables low-noise servo control of lasers and other experimental systems. The PI2D loop filter, with two-stage integral feedback, provides tight locking to cavities and atomic/molecular transitions with full user control over the loop-filter parameters.
The D2-135 Offset Phase Lock Servo precisely controls and quickly adjusts the frequency detuning between a master and a follower laser, from 250 MHz to 9.3 GHz. The D2-135 forms a complete offset lock system when combined with the D2-250 Heterodyne Module and D2-260 Beat Note Detector.
⚙ hardware
The optical frequency discriminator (OFD) system of SILENTSYS smartly delivers a voltage signal that is proportional to the fluctuations of the optical frequency of the input laser beam. This turn-key module is suitable for laser frequency noise characterization and/or for laser frequency stabilization to drastically reduce its optical linewidth. The OFD features ultralow noise performances being successful in achieving frequency noise level as low as 0.01 Hz²/Hz with >60 dB noise reduction, and that is achieved in a compact and user-friendly package. This product is available in a huge wavelength range from UV, VIS to NIR, with one or two optical modules inside to be a very versatile tool.
The optical frequency correlator (OFC) system contains a common 2-input optical frequency discriminator (OFD). This makes it possible to frequency.stabilize two wavelength distant lasers onto the same optical reference in order to reduce their frequency fluctuations and to correlate them precisely.
Based on this fact, the optical beat frequency between the two stabilized lasers generates THz or GHz signals that reach a very low frequency noise level and are easily frequency tunable. Moreover, as a standard OFD, it smartly delivers a voltage signal that is proportional to the frequency fluctuations of the input laser beam. This turn-key device is suitable for laser frequency noise characterization and/or for laser frequency stabilization.
⚙ hardware
Our sensitive and compact, HighFinesse/Ångstrom’ wavelength meters deliver high speed wavelength measurements of pulsed and continuous laser with absolute accuracy down to 2 MHz. A wide variety of models is available, covering wavelength ranges from 192 nm up to 11000 nm. The devices can not only accurately measure wavelengths, but can with their output used to stabilize a laser such that its emission wavelength remains very stable.
To fully meet the increasing demand of flexibility and integration of laser test equipment, the HighFinesse world famous WS wavemeters are available as rack and standalone systems. The latter do not require an external computer. They can be controlled locally by connecting screen, keyboard, mouse or via touch screen (not available for all models) and using Ethernet connection via the DLL-based API or SCPI commands.
Bibliography
| [1] | A. D. White, “Frequency stabilization of gas lasers”, IEEE J. of Quantum Electronics 1 (8), 349 (1965); doi:10.1109/JQE.1965.1072246 |
|---|---|
| [2] | T. W. Hänsch and B. Couillaud, “Laser frequency stabilization by polarization spectroscopy of a reflecting reference cavity”, Opt. Commun. 35 (3), 441 (1980) (Hänsch–Couillaud technique); doi:10.1016/0030-4018(80)90069-3 |
| [3] | R. W. P. Drever, J. L. Hall et al., “Laser phase and frequency stabilization using an optical resonator”, Appl. Phys. B 31, 97 (1983); doi:10.1007/BF00702605 |
| [4] | G. C. Bjorklund et al., “Frequency-modulation (FM) spectroscopy”, Appl. Phys. B 32 (3), 145 (1983); doi:10.1007/BF00688820 |
| [5] | C. Salomon et al., “Laser stabilization at the millihertz level”, J. Opt. Soc. Am. B 5 (8), 1576 (1988); doi:10.1364/JOSAB.5.001576 |
| [6] | J. Dirscherl et al., “A dye laser spectrometer for high resolution spectroscopy”, Opt. Commun. 91, 131 (1992); doi:10.1016/0030-4018(92)90114-7 |
| [7] | T. Day et al., “Sub-hertz relative frequency stabilization of two diode laser-pumped Nd:YAG lasers locked to a Fabry–Pérot interferometer”, IEEE J. Quantum Electron. 28 (4), 1106 (1992); doi:10.1109/3.135234 |
| [8] | N. Uehara and K. I. Ueda, “193-mHz beat linewidth of frequency-stabilized laser-diode-pumped Nd:YAG ring lasers”, Opt. Lett. 18 (7), 505 (1993); doi:10.1364/OL.18.000505 |
| [9] | C. C. Harb et al., “Suppression of the intensity noise in a diode-pumped neodymium:YAG nonplanar ring laser”, IEEE J. Quantum Electron. 30 (12), 2907 (1994); doi:10.1109/3.362718 |
| [10] | S. Seel et al., “Cryogenic optical resonators: a new tool for laser frequency stabilization at the 1 Hz level”, Phys. Rev. Lett. 78 (25), 4741 (1997); doi:10.1103/PhysRevLett.78.4741 |
| [11] | Y. Shevy and H. Deng, “Frequency-stable and ultranarrow-linewidth semiconductor laser locked directly to an atom-cesium transition”, Opt. Lett. 23 (6), 472 (1998); doi:10.1364/OL.23.000472 |
| [12] | D. A. Shaddock, M. B. Gray and D. E. McClelland, “Frequency locking a laser to an optical cavity using spatial mode interference”, Opt. Lett. 24 (21), 1499 (1999); doi:10.1364/OL.24.001499 |
| [13] | B. C. Young et al., “Visible lasers with subhertz linewidths”, Phys. Rev. Lett. 82 (19), 3799 (1999); doi:10.1103/PhysRevLett.82.3799 |
| [14] | S. Kasapi et al., “Sub-shot-noise frequency-modulation spectroscopy by use of amplitude-squeezed light from semiconductor lasers”, J. Opt. Soc. Am. B 17 (2), 275 (2000); doi:10.1364/JOSAB.17.000275 |
| [15] | E. D. Black, “An introduction to Pound–Drever–Hall laser frequency stabilization”, Am. J. Phys. 69 (1), 79 (2001); doi:10.1119/1.1286663 |
| [16] | B. J. J. Slagmolen et al., “Frequency stability of spatial mode interference (tilt) locking”, IEEE Journal of Quantum Electronics 38 (11), 1521 (2002); doi:10.1109/JQE.2002.804267 |
| [17] | F. W. Helbing et al., “Carrier–envelope offset phase-locking with attosecond timing jitter”, J. Sel. Top. Quantum Electron. 9 (4), 1030 (2003); doi:10.1109/JSTQE.2003.819104 |
| [18] | St. A. Webster et al., “Subhertz-linewidth Nd:YAG laser”, Opt. Lett. 29 (13), 1497 (2004); doi:10.1364/OL.29.001497 |
| [19] | J. Rollins et al., “Solid-state laser intensity stabilization at the 10−8 level”, Opt. Lett. 29 (16), 1876 (2004); doi:10.1364/OL.29.001876 |
| [20] | H. Stoehr et al., “Diode laser with 1 Hz linewidth”, Opt. Lett. 31 (6), 736 (2006); doi:10.1364/OL.31.000736 |
| [21] | F. Seifert et al., “Laser power stabilization for second-generation gravitational wave detectors”, Opt. Lett. 31 (13), 2000 (2006); doi:10.1364/OL.31.002000 |
| [22] | F. Kéfélian et al., “Ultralow-frequency-noise stabilization of a laser by locking to an optical fiber-delay line”, Opt. Lett. 34 (7), 914 (2009); doi:10.1364/OL.34.000914 |
| [23] | P. Kwee et al., “Shot-noise-limited laser power stabilization with a high-power photodiode array”, Opt. Lett. 34 (19), 2912 (2009); doi:10.1364/OL.34.002912 |
| [24] | N. Satyan et al., “Phase noise reduction of a semiconductor laser in a composite optical phase-locked loop”, Opt. Eng. 49 (12), 124301 (2010); doi:10.1117/1.3518077 |
| [25] | Y. Zhao et al., “Sub-Hertz frequency stabilization of a commercial diode laser”, Opt. Commun. 283, 4696 (2010); doi:10.1016/j.optcom.2010.06.079 |
| [26] | P. Kwee, B. Willke and K. Danzmann, “New concepts and results in laser power stabilization”, Appl. Phys. B 102 (3), 515 (2011); doi:10.1007/s00340-011-4399-1 |
| [27] | M. Jing et al., “High bandwidth laser frequency locking for wideband noise suppression”, Opt. Express 29 (5), 7916 (2021); doi:10.1364/OE.419832 |
| [28] | M. T. Nery et al., “Laser power stabilization via radiation pressure”, Opt. Lett. 46 (8), 1946 (2021); doi:10.1364/OL.422614 |
| [29] | W. Jin et al., “Hertz-linewidth semiconductor lasers using CMOS-ready ultra-high-Q microresonators”, Nature Photonics 15, 346 (2021); doi:10.1038/s41566-021-00761-7 (correction: doi:10.1038/s41566-021-00805-y) |
| [30] | N. Chabbra et al., “High stability laser locking to an optical cavity using tilt locking”, Opt. Lett. 46 (13), 3199 (2021); doi:10.1364/OL.427615 |
| [31] | B. Li et al., “Reaching fiber-laser coherence in integrated photonics”, Opt. Lett. 46 (20), 5201 (2021); doi:10.1364/OL.439720 |
| [32] | T. Cullen et al., “Passive laser power stabilization via an optical spring”, Opt. Lett. 47 (11), 2746 (2022); doi:10.1364/OL.456535 |
| [33] | N. Jiao et al., “Passive laser power stabilization in a broadband noise spectrum via a second-harmonic generator”, Opt. Lett. 49 (13), 3568 (2024); doi:10.1364/OL.524119 |
| [34] | N. Kolodzie, I. Mirgorodskiy, C. Nölleke and P. O. Schmidt, “Ultra-low frequency noise external cavity diode laser systems for quantum applications”, Opt. Express 32 (17), 29781 (2024); doi:10.1364/OE.530087 |
| [35] | J. Zenner, K. U. Schreiber and S. Stellmer, “Stabilizing the free spectral range of a large ring laser”, Opt. Lett. 50 (6), 1763 (2025); doi:10.1364/OL.550265 |
| [36] | R. Paschotta, “Noise in Laser Technology”. Part 1 — Intensity and Phase Noise; Part 2: Fluctuations in Pulsed Lasers; Part 3: Beam Pointing Fluctuations |
(Suggest additional literature!)
Questions and Comments from Users
Here you can submit questions and comments. As far as they get accepted by the author, they will appear above this paragraph together with the author’s answer. The author will decide on acceptance based on certain criteria. Essentially, the issue must be of sufficiently broad interest.
Please do not enter personal data here. (See also our privacy declaration.) If you wish to receive personal feedback or consultancy from the author, please contact him, e.g. via e-mail.
By submitting the information, you give your consent to the potential publication of your inputs on our website according to our rules. (If you later retract your consent, we will delete those inputs.) As your inputs are first reviewed by the author, they may be published with some delay.