A partnership between dynamin and lipids defines dynamics and intermediates of membrane fission (original) (raw)
. Author manuscript; available in PMC: 2009 Dec 26.
SUMMARY
The GTPase dynamin is critically involved in membrane fission during endocytosis. How does dynamin use the energy of GTP hydrolysis for membrane remodeling? By monitoring the ionic permeability through lipid nanotubes (NT) interacting with dynamin and GTP we detected cyclic localized squeezing and relaxation of NT, ultimately yielding leak-free fission stochastically. Our calculations revealed that critical local narrowing of NT induces cooperative lipid tilting, leading to self-merger of the inner monolayer of NT (hemi-fission), consistent with the absence of leakage. We found that dynamin pre-assembled on NT without GTP produces stable curvature which, depending upon lipid composition, approaches the hemi-fission threshold. GTP addition causes gradual disassembly of dynamin, triggering either spontaneous fission or curvature relaxation. We propose that dynamin transmits GTP’s energy to periodic curvature stress caused by an assembly of a limited curvature scaffold, which next relaxes and rewinds to its initial state upon cooperative GTP hydrolysis.
INTRODUCTION
Formation of an endocytic vesicle is completed by scission of a thin membrane neck connecting the vesicle and the plasma membrane (De Camilli et al., 1995; Eliasson et al., 1996; Frolov et al., 2003b; Rosenboom and Lindau, 1994). Though scission is intuitively associated with cutting and resealing, even transient permeabilization of cellular membranes could be damaging, especially for small vesicles whose content quickly escape through even minute pores (Frolov et al., 2003a). Thus, fission of neck membranes is more likely to proceed via “hemi-fission” to avoid leakage (Chernomordik and Kozlov, 2003). The neck fission involves extensive bending deformations (Kozlovsky and Kozlov, 2003) conducted by a specialized protein machinery assembled on the membrane neck, where the GTPase dynamin is a key component (Conner and Schmid, 2003; Hinshaw, 2000; Hinshaw and Schmid, 1995). Crucial for many cell processes featuring fission, dynamin family members form dense collars around necks of budding vesicles and dividing organelles (Hinshaw and Schmid, 1995; Praefcke and McMahon, 2004). Assembly of this collar triggers cooperative GTP hydrolysis, which is thought to force membrane remodeling (Marks et al., 2001; Sweitzer and Hinshaw, 1998). However, the pathway that links the GTPase activity of dynamin and membrane rearrangements during fission is obscure.
The strongest experimental data supporting the hypothesis of a direct mechano-chemical action of dynamin are based upon analysis of dynamin’s interaction with pure lipid membranes. Isolated dynamin remains mechanically active in vitro: it causes tubulation of charged lipid bilayers via self-assembly into long cylindrical superstructures, showing a pronounced helical pattern of dynamin packing (Marks et al., 2001; Stowell et al., 1999; Zhang and Hinshaw, 2001), and fragmentation of such tubes upon GTP hydrolysis (Roux et al., 2006; Sweitzer and Hinshaw, 1998). Tube fragmentation is generally linked to the cooperative reorganization of the helix upon GTP hydrolysis: constriction, extension and twisting of the dynamin helix have all been proposed to impose curvature and tensile stresses on the tube membrane (Roux et al., 2006; Stowell et al., 1999). Whether similar long-range transformations of dynamin helices catalyze rearrangements of cellular membrane necks remains unclear.
In the presence of GTP, dynamin polymerizes only transiently on liposome templates: cooperative GTP hydrolysis, triggered by polymerization (Warnock et al., 1996) leads to disordering and disassembly of the dynamin scaffold preventing formation of extended structures (Stowell et al., 1999; Ramachandran and Schmid, 2008). In cells, dynamin is efficiently and transiently targeted to membrane necks, where it is thought to quickly mediate their scission (Rappoport et al., 2008; Merrifield et al., 2005; Praefcke and McMahon, 2004). Long membrane necks covered by dynamin are only seen when the fission activity of dynamin is suppressed, e.g. by addition of non-hydrolysable analogues of GTP or by overexpression of specific mutants of dynamin (Takei et al., 1995). These observations suggest that a short dynamin collars formed when GTP is constantly present, suffice to mediate membrane fission.
The dynamics of membrane remodeling by short dynamin assemblies formed in the presence of GTP is difficult to characterize as the corresponding membrane transformations are expected to be fast and highly localized. In cellular systems similar membrane transformations are studied by electrophysiology revealing a rich dynamic behavior of membrane necks of endocytic vesicles (Frolov et al., 2003b; Eliasson et al., 1996; Suss-Toby et al., 1996; Rosenboom and Lindau, 1994). Here we resolved dynamin’s interaction with cylindrical nanotubes pulled from lipid membranes (Frolov et al., 2003b). We measured the permeability of the tube’s interior to estimate average changes in the diameter of the tube and to resolve the kinetics of tube fission. We discovered that the dynamin coat was capable of squeezing membrane tubes to extremely small radii, depending on the tube rigidity. However, long dynamin scaffolds did not trigger fission: instead fission followed GTPase-dependent cycles of assembly and disassembly of short dynamin coats and involved a stochastic process dependent on the curvature stress imposed by dynamin. These results suggest that dynamin acts as a catalyst of membrane remodeling bringing lipids to an unstable intermediate via creation of regulated curvature constraints.
RESULTS
Voltage-clamp conductance measurements on lipid nanotubes
Lipid nanotubes were pulled from planar phospholipid bilayers using a glass pipette so that the nanotube extended between the bilayer and the pipette tip (Figure 1A; Frolov et al., 2003b). The nanotubes were formed in ionic buffer and the integral ionic permeability (hereafter conductance, G) of the tube interior was monitored in real time. The luminal radius (RL) of a nanotube pulled from a lipid bilayer is defined by mechanical equilibrium between the lateral tension (σ) and the bending rigidity (B) of the tube membrane (RL~√B/σ) and thus does not depend on the tube length L (Evans and Yeung, 1994; Supp. Data). Measuring the dependence of G on L gives RL (Figure 1B). To obtain different RL, we used lipid compositions which differ substantially in their bending rigidity. The first produced narrow nanotubes (NT) (RL=6.0±1.2 nm, SD, n=21). The second produced wide nanotubes (wNT) (RL=20.5±2.2 nm, SD n=6) (Figure 1B). We estimated lateral tension of NT as 0.7±0.2 dyn/cm and of wNT as 0.4±0.2 dyn/cm (Supp. Figure 1). This difference and ~6 times higher bending rigidity of wNT membrane containing lysolipids and cholesterol (Supp. Data, “Estimation of the lateral tension of the NT and wNT membranes”; Frolov et al., 2003b) account for larger value of the wNT radius. Both NT and wNT were used as templates for dynamin.
Figure 1. Formation of NT and wNT from a planar phospholipid bilayer.
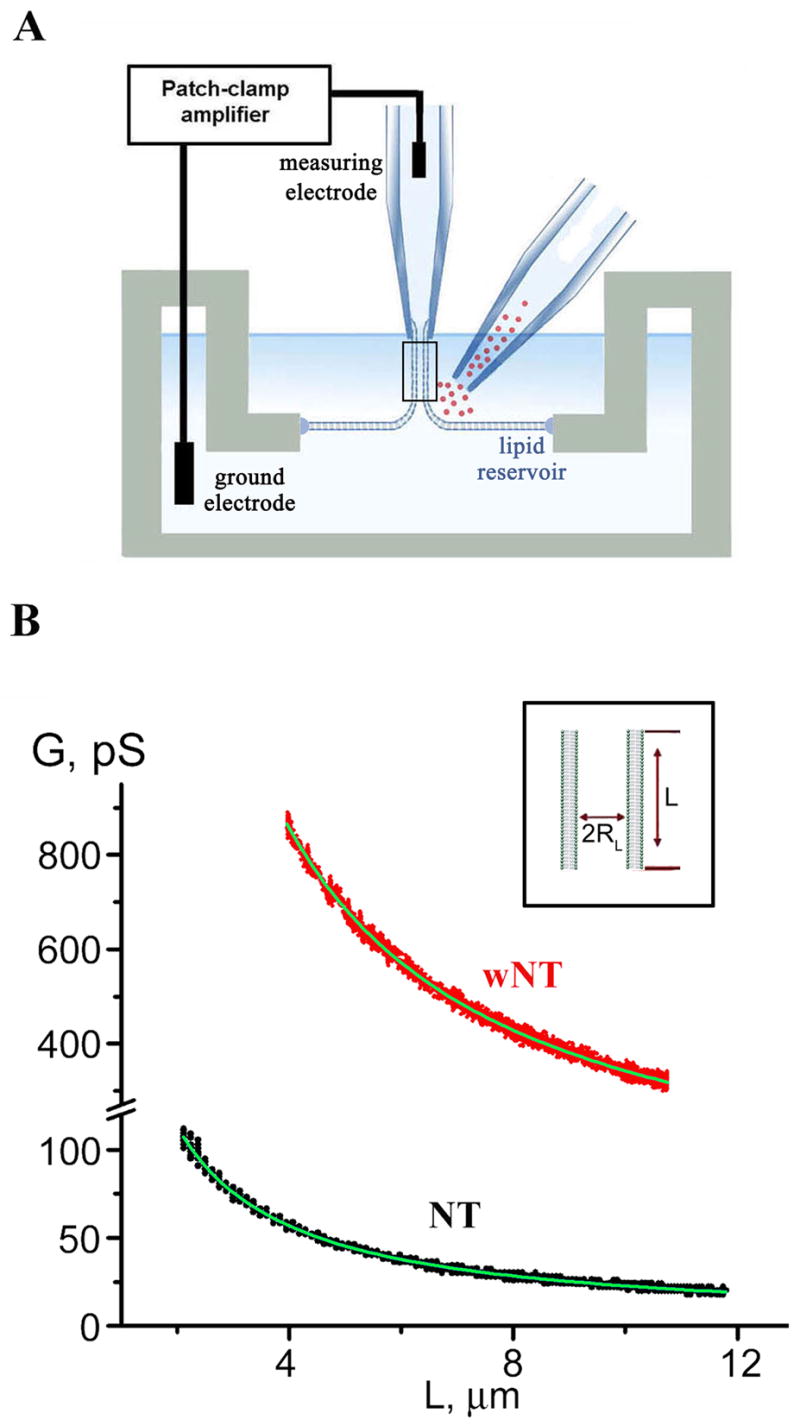
A. Illustration of a nanotube formation from planar bilayer by patch-pipette. Nanotube conductance (GNT) is determined by measuring the current resulting from application of a constant potential between measuring and ground electrodes (Frolov et al., 2003b); a pipette used to deliver chemicals directly to the nanotube is shown on the right. B. GNT measured in picosiemens (pS), depends hyperbolically on nanotube length (L); the fitting function G(L)=π_RL_2/(σ·(L+Loffset)) (where σ=100 Ohm·cm is the specific resistance of the ionic buffer used and Loffset is the length offset due to pipette positioning) was used to determine the luminal radius (RL) of nanotubes of different lipid composition (NT, black, and wNT, red; the fit results shown in green); insert outlines nanotube geometry.
Lipid-dependent generation of membrane curvature by dynamin
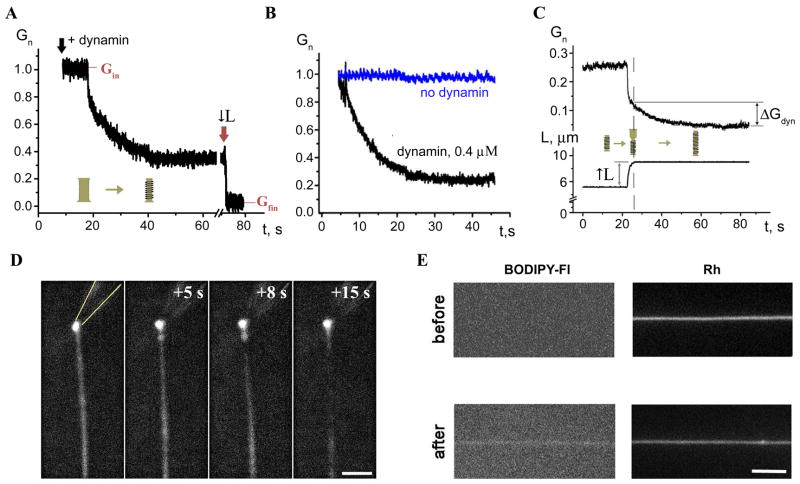
Shortly after application of 4 μM dynamin solution from a delivery pipette (Figure 1A), the NT conductance gradually decreased reaching a new stationary level (Figure 2A, in 5 out of 5 experiments). The conductance decrease indicates narrowing of NT, presumably caused by assembling of dynamin helices. Removal of the delivery pipette did not lead to restoration of the NT conductance, thus dynamin binds strongly to the tube wall. We interpret the subsequent resistance to NT shortening as the assembly of an extended dynamin scaffold. Unlike the bare NT, that could be shortened and extended freely, the NT coated by dynamin was usually severed upon shortening, detected by an instant and irreversible drop of the NT conductance to background level (Figure 2A, ↓L-arrow).
Figure 2. Interaction of dynamin with NT.
A. Decrease of normalized conductance (Gn) of NT upon application of dynamin. Gn=(G−G0)/(Ginit−Go), where Ginit is the nanotube conductance before dynamin application, G0 is the background conductance and G is the measured conductance; upon reaching steady-state, an attempt to shorten NT (↓L arrow) resulted in NT breakage. B. Immediate decrease of the NT conductance (black) formed in the presence of dynamin; blue curve illustrates the behavior of NT without dynamin. C. Extension of NT “squeezed” by dynamin (↑L) caused two effects: first, a new piece of a bare NT was added seen as initial conductance drop; second, this new part of NT was slowly squeezed by dynamin producing additional conductance decrease (ΔGdyn). D. Fluorescence micrographs showing outcomes of dynamin adsorption on a nanotube pulled from a GUV containing 0.5 mol% of Rh-DOPE. The pulling pipette is outlined in the first panel; t=0 corresponds to the dynamin application; bar 5 μm. E. Fluorescent micrographs showing adsorption of BODIPY-Fl-labeled dynamin on a nanotube pulled from a GUV containing Rh-DOPE; images of BODIPY-Fl (left) and Rh (right) fluorescence taken before and 5 minutes after protein application; bar 5 μm.
To minimize the concentration variability, we pulled NT in the constant presence of dynamin (0.4 μM) in solution. Immediately after NT formation, dynamin assembling on the tubule caused a gradual reduction of the NT conductance (Figure 2B, 12 experiments in total). After reaching a new steady-state, further extension of the NT was still possible: when a new piece of the bare NT was pulled out, dynamin quickly bound and squeezed it (Figure 2C, 3 experiments in total).
Figure 3. Lipid dependence and critical character of the squeezing of lipid nanotubes by dynamin.
A. Dynamin-induced decrease of normalized conductance (Gn, see Figure 2) of NT and NT containing 1 mol% PI(4,5)P2 (black and brown curves respectively, lower time scale) and wNT (red, upper time scale). B. Histogram showing characteristic times of nanotube squeezing by dynamin (black bars for NT, n=17; red bars for wNT, n=6; brown bars for NT with PI(4,5)P2, n=3) and hydrostatic pressure (blue bar for NT, n=5); error bars represent SD. C. Histogram demonstrating the averaged luminal radius of bare nanotubes and nanotubes squeezed by dynamin or osmotic pressure estimated from their conductance (black bars for NT, n=12; red bars for wNT, n=6; brown bars for NT with PI(4,5)P2, n=3; blue bar for NT squeezed by osmotic pressure, n=5), error bars show SD; insert demonstrates scaled shapes of NT and wNT squeezed by dynamin. Geometrical parameters of the dynamin spiral are from Sweitzer and Hinshaw, 1998, bilayer thickness is 4nm. D. Effect of osmotic pressure on NT conductance; blue curve –negative pressure inside tube (~0.8 Osm), green curve – positive pressure (~0.2 Osm).
To verify that dynamin can bind to the NT membrane containing no PI(4,5)P2, we monitored dynamin interaction with membrane tubes pulled from giant unilamellar vesicles (GUV) containing a moderate amount of PS (20 mol%). Dynamin produced visible squeezing of such tubes as detected by reduction of the peak fluorescence averaged over the tube length (1.9±0.8-fold, SD, n=4; Figure 2D). Furthermore, fluorescently labeled dynamin densely covers the membrane tubes containing 20 mol% PS (Figure 2E). The increase of the BODIPY fluorescence associated with the tube (at least 3 times higher than the background noise) was detected in 5 out of 5 trials. Thus, dynamin indeed interacts with lipid nanotubes containing a moderate amount of PS.
However, the action of dynamin on lipid nanotubes was strongly modulated by PI(4,5)P2 and membrane rigidity. Figure 3A shows representative recordings demonstrating the dynamin-induced decrease of the conductance of NT, NT doped with PI(4,5)P2 and wNT. PI(4,5)P2 greatly accelerated the squeezing process (Figure 3A, B; brown). The wNT conductance, on the other hand, decreased much slower (Figure 3A, B; red), likely reflecting dynamin’s binding preference for highly curved PI(4,5)P2-containing membranes (Ramachandran and Schmid, 2008).
The conductance of the nanotube, normalized to its initial value, reached a similar steady-state value independently on the lipid composition (Figure 3A). However, the luminal radius corresponding to this new steady-state was substantially different for NT and wNT (Figure 3C). Assuming that the nanotubes were uniformly covered and squeezed by dynamin (Figure 2E), we found that the NT RL decreased to 2.6±0.4 nm (Figure 3B, black columns) while the wNT was squeezed to 12±2 nm (Figure 3C, red columns). Addition of PI(4,5)P2 caused only minor effect on RL (Figure 3C, brown columns). The scaled images illustrating the geometry of NT and wNT squeezed by dynamin are shown in the insert, Figure 3C. The outer diameter of the squeezed NT (~ 40 nm) and wNT (~60 nm) are not substantially different, comparable to those from structural studies (Sweitzer and Hinshaw, 1998; Zhang and Hinshaw, 2001), confirming the validity of these measurements. However, the luminal diameters of NT and wNT are drastically different. This difference demonstrates that the curvature-driven activity of dynamin can be strongly modulated by membrane lipid composition. Thus, the dynamin scaffold cannot impose the same geometry on every lipid membrane (Kozlov, 2001): more rigid membranes bend less.
The inner diameter of the NT squeezed by dynamin was comparable with the membrane thickness, indicating possible curvature instabilities (Allain et al., 2004; Kozlovsky and Kozlov, 2003; Jan Bukman et al., 1996). To examine stability of NT at high curvatures, we used osmotic pressure. High and low salt solutions were applied to the NT (Figure 1A, Supp. Figure 2). External application of hypotonic solutions to NT led to a moderate expansion of the NT (Figure 3D, green curve). Hypertonic solutions caused a gradual squeezing, mimicking the action of dynamin (Figure 3D, blue curve). Upon reaching RL comparable with those of the NT squeezed by dynamin (see histogram in Figure 3C), osmotically stressed NT collapsed (in 5 out of 8 experiments; Figure 3D, blue curve,). These data establish that a curvature stress close to that imposed by the dynamin scaffold destabilizes the bare lipid NT (Jan Bukman et al., 1996). Thus, while the dynamin scaffold can generate potentially destabilizing high membrane curvature it unexpectedly stabilizes narrow NT from fission.
Non-leaky fission of lipid nanotubes by dynamin and GTP
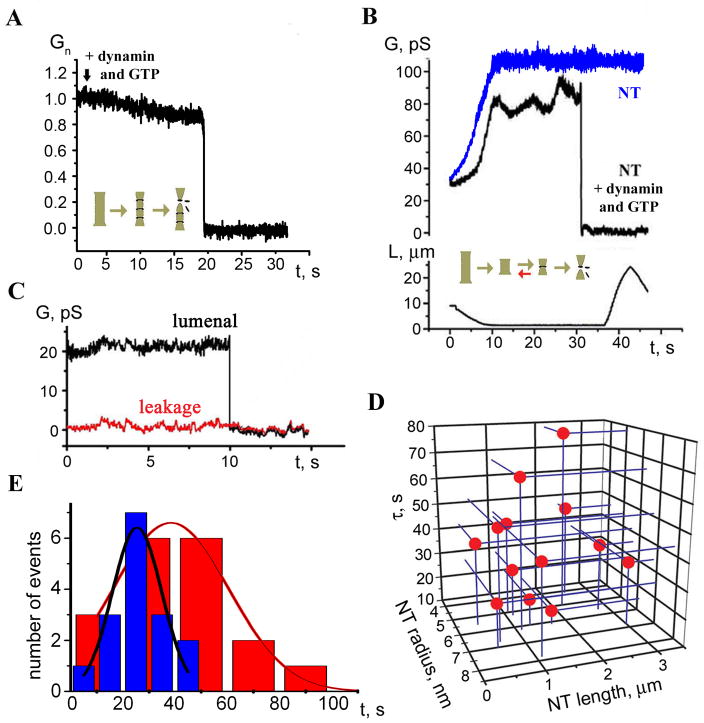
In cells, dynamin acts in the presence of GTP required for the fission activity, so we next investigated the effects of GTP NTs formed in the presence of dynamin (0.4 μM) and GTP (1 mM) behaved differently from NTs generated without GTP: we observed only a minor gradual decrease in GNT terminated by an instantaneous drop to background level (Figure 4A, 14 out of 17 experiments). We interpret these acute conductance drops as a complete loss of connectivity through NT because i) their kinetics were much faster than dynamin-induced tube squeezing (Figure 2A); ii) the NT conductance did not change when the patch pipette was moved to impose different lengths (Figure 4B). When GTPγS replaced GTP, a gradual conductance decrement was detected instead of the instantaneous conductance drops (4 experiments, not shown), confirming that the NT closure required GTP hydrolysis. This irreversible closure of the NT indicates complete fission rather than merger of only the inner monolayer of the NT membrane (stable hemi-fission), as the hemi-fission intermediate is expected to spontaneously decay to complete fission for NTs under high lateral tension (Kozlovsky and Kozlov, 2003).
Figure 4. Non-leaky fission of NT by dynamin and GTP.
A. Simultaneous addition of dynamin and GTP to NT caused a small gradual decrease of NT normalized conductance followed by instantaneous NT breakage. B. Waves of conductance fluctuations preceding the fission of NT shortened to ~1 μm length in the presence of dynamin and GTP; fission is seen as an abrupt conductance drop; NT shortened to similar length without dynamin was stable (blue curve). C. Simultaneous measurements of the GNT (integral conductance through NT lumen, black curve) and the conductance of its membrane corresponding to leakage through NT wall (red curve). D. Scatter plot showing the dependence of NT lifetime (upon the dynamin and GTP application) on NT length and radius. E. Life time distribution of shortened NT (as in 4B) in the presence of dynamin and GTP (red), compared to the distribution of the characteristic time of NT squeezing by dynamin (blue).
We further monitored whether NT closure was accompanied by leakage. The NT conductance was measured simultaneously with the current through the NT membrane. In previous studies (Frolov et al., 2003a), the sensitivity of such measurements (background noise of 20–50 pS r.m.s. at ~0.5 ms time resolution) allowed us to detect small and transient pores in the membrane during leaky membrane fusion. No such pores were detected during the dynamin-driven closure of the NT in 5 out of 5 experiments (Figure 4C). The lack of detectable leakage strongly indicates that the dynamin-driven fission of the NT involves the hemi-fission intermediate. Interestingly, no spikes in the NT conductance accompanied the osmotic-driven fission of the NT (in 5 out of 5 cases, see Figure 3D) while such spikes, indicating the membrane leakage, were routinely detected when the NT was severed mechanically (Supp. Figure 3). Thus, the absence of the leakage during fission seemingly correlates with the critical squeezing of NT.
Lack of pronounced narrowing of the NT prior to fission suggests that in the presence of GTP dynamin acts in small assemblies. To explore this possibility, we performed experiments on short NTs formed in the presence of dynamin (0.4 μM) and GTP (1 mM). The NTs were first pulled and then quickly shortened before dynamin-mediated fission had occurred. The shortening is seen as an increase of the NT conductance coinciding with the decrease of the NT length (Figure 4B). With no dynamin present, the NT shortened up to 0.5 μm had the conductance stable in time (Figure 4B, blue curve). When the NTs were shortened to less than 0.8 μm in the presence of dynamin and GTP (5 cases in total), we detected slow wave-like conductance fluctuations followed by fission (Figure 4B, black curve). For longer NTs such fluctuations were not resolved.
There are two characteristic time scales for the NT conductance (Figure 4B). Slow wave-like events reflect reversible changes in the NT geometry. Fast conductance drops indicate the fission exclusively. The distribution of the life-time of shortened NT (the lag time before the fission) was rather broad (Figure 4D) and showed no apparent correlation with NT length or radius, indicating the probabilistic nature of the NT fission. We further compared the life-time of the shortened NT with the characteristic time of squeezing of long (> 3 μm) NTs by dynamin in the absence of GTP (Figure 4E, red and blue respectively). This comparison shows that the lifetime of a short NT is often longer than the time needed to completely encage a long NT by dynamin. Yet, only minor narrowing of the NT was detected prior to the fission (Figure 4A, B, see also the histogram in Figure 5C). Thus, we deduce that GTP hydrolysis, triggered by self-assembly of a short dynamin scaffold, can result in either fast irreversible fission or slower reversible disassembly of dynamin without producing fission. Only a part of the NT membrane is covered by assembled dynamin scaffolds in each particular moment. Such an incomplete coverage of NT in the presence of GTP would well correspond to the “loose” and fragmented dynamin spirals seen by electron microscopy (Stowell et al., 1999).
Figure 5. Relaxation of pre-assembled dynamin scaffold by GTP.
A. Simultaneous addition of dynamin and GTP caused a slight gradual narrowing of wNT (red). At the new steady-state a decrease of wNT length (black) leads to the increase of its normalized conductance (Gn) indicating that wNT is not constrained by dynamin (see Figure 1C); B. Addition of GTP to “squeezed” nanotubes triggers an increase of both NT (black) and wNT (red) conductances. NT broke after a period of expansion, while wNT remained stable and was rapidly squeezed upon removal of GTP. C. Histogram showing steady-state conductance of NT (black) and wNT (red) upon addition of dynamin alone (dyn), GTP to nanotubes squeezed by dynamin (dyn, then GTP), dynamin and GTP (dyn+GTP) and dynamin and GDP (dyn+GDP); for dynamin and GTP the NT conductance was averaged near the fission point, error bars show SE. D. Effect of dynamin on the NT conductance is nucleotide-dependent: GTP stimulates fast fission of NT (black); GDP impairs both fission and curvature activities of dynamin.
The transient formation of short dynamin scaffolds is expected to cause periodic variations of the nanotube conductance, and these were observed (Figure 4B). We calculated that localized squeezing of the NT lumen to 2 nm by a short collar-like dynamin structure (corresponding roughly to 3 rungs of a dynamin spiral or 40 nm length (Zhang and Hinshaw, 2001)) would result in ~ 10 pS change in GNT, providing that NT length is diminished to ~1 μm. Changes of this magnitude were seen (Figure 4B). Thus, when GTP is present in solution, dynamin operates in short and transient assemblies, each attempting to mediate a localized fission reaction.
Dynamin mediates membrane fission in a nucleotide and lipid dependent manner
To explore the effect of lipid composition on fission by short dynamin assemblies and GTP, we applied dynamin and GTP to wNT. We detected no breakage of wNT but only a moderately slow decrease of its conductance to a new steady-state level (Figure 5A) in 6 out of 6 experiments where dynamin (0.4 μM) and GTP (1 mM) were added together. The corresponding steady-state conductance was twice higher with GTP than without it (Figure 3A, 5B), suggesting that the assembled structures were short and did not cover the wNT completely. Indeed, under these conditions dynamin did not restrict the wNT geometry and its conductance could be experimentally manipulated (Figure 5A). This behavior further supports that, in the presence of GTP, dynamin molecules acted in small assemblies, as no extended curvature scaffold was formed.
The stationary conductance of wNT in the presence of dynamin and GTP is expected to be the same, regardless of the direction of approach to the steady state. To confirm this conjecture, wNT were pulled in the presence of dynamin (0.4 μM) and then, after the wNT squeezing by dynamin was completed, GTP (1 mM) was applied via a delivery pipette. Subsequently, the wNT conductance increased to the new stationary value similar to that achieved upon simultaneous addition of dynamin and GTP to wNT (Figure 5B, red curve). After removal of the delivery pipette, the wNT conductance returned to the level characteristic for dynamin squeezing in the absence of GTP (Figure 5B, C). Thus GTP regulates dynamin’s function not only in membrane fission, but also in curvature scaffolding.
Upon addition of GTP to dynamin preassembled onto NT, we observed the conductance increase indicating, as with wNT, the curvature relaxation (Figure 5B, black curve). In contrast to wNT, however, the relaxation was followed by the NT fission (5 of 5 experiments). This difference in NT and wNT response to GTP establishes that dynamin-mediated fission is lipid dependent.
The NT conductance, right before the drop, reached a level about twice higher than the conductance of dynamin-coated NT (Figure 5C). Thus, the primary response to GTP addition is the destabilization of the assembled dynamin scaffold. The scaffold becomes softer, presumably due to weakening of the stacking interactions between the dynamin molecules (Ramachandran and Schmid, 2008). Interestingly, we found that in the presence of GDP dynamin produces only moderate squeezing of the NT (Figure 5C, D). Thus the softening of the dynamin scaffold upon GTP hydrolysis could be related to impaired curvature activity of dynamin in GDP-bound state.
Theoretical analysis of the fission pathway
To explore the detected probabilistic nature of the fission events and the apparent need for localized, GTP-dependent dynamin assembly and disassembly, we further analyzed theoretically four of our findings: 1) Dynamin produces high membrane curvature comparable to that generated by non-enzymatic protein domains (e.g. N-BAR, Gallop et al., 2006). Thus it does not need GTP hydrolysis to bring NT close to the point of curvature instability where no more bending is required to initiate fission (as compared with osmotic-driven fission, Figure 3). 2) GTP hydrolysis causes almost no additional thinning of NT or wNT squeezed by dynamin (Figure 5C). 3) GTP hydrolysis results in either fission or tube expansion (Figure 5C). 4) Fission is a local event as no long curvature scaffolds are formed when dynamin and GTP are added together (Figure 4A, 5A).
Accordingly, we consider a short piece of NT encaged by a dynamin scaffold (Figure 6A). This configuration is stable until GTP is added. Recent kinetic studies have shown that upon GTP hydrolysis the membrane is released from dynamin scaffolds more rapidly than they disassemble (Ramachandran and Schmid, 2008). Thus, it is possible that for some time the dynamin scaffold preserves its integrity, while the encaged membrane detaches and is free to find a way to release the curvature stress so as to minimize energy (Figure 6A).
Figure 6. Theoretical analysis of local membrane rearrangements by dynamin.
A. The pathway of membrane rearrangement leading to the fission of a short membrane neck detached from a dynamin scaffold (blue) upon GTP hydrolysis; upper half of the neck membrane is shown. The neck constriction is followed by rearrangement of the thinnest part of the neck: lipids, by synchronous tilting, expose a small part of the hydrophobic membrane interior (hydrophobic belt). If the radius of the neck at the mid-point (Rmid) is small enough, expansion of the belt correlated with thinning of the neck (see 6D) becomes possible and the neck closes completely. The neutral surface (Kozlovsky and Kozlov, 2003) of the inner monolayer of the neck membrane is shown by the red line. The function R(L) describes the shape of this surface in the coordinate system (R, L); the coordinate center is placed in the midst of the neck (where Rmid is measured), so that the total length of the detached neck is 2_L0_. This length and the radius of the neck at both ends (R0) are fixed by the dynamin scaffold (note that R0 equals the radius of the nanotube in the dynamin-squeezed state and is about 0.5nm bigger than the luminal radius, R_L_). B. Calculated shapes of necks (R(L)) detached from the dynamin scaffold of different initial length (L0). Necks shorter than a critical length Lc (see 6C) narrow (Rmid<R0) while longer necks bulge; calculated 3D shapes of shortest and longest necks are shown. C. Numerically calculated dependence of the Rmid of the neck length L0 for NT and wNT. From this dependence the minimal radius of the neck (Rmin) and the critical length Lc (at which _Rmid_=R0) are determined. D. Energy diagram showing the dependence of free energy of the neck (_R0_=2nm) upon the width (H) and the radius (Rmid) of the hydrophobic belt. The energy barrier along the pathway indicated by the red arrow is ~35kBT. E. Dependence of the critical length, Lc, (blue) and the neck radius in the narrowest place, Rmin, (black) on R0.
The new stationary shape which the detached membrane piece, the neck, attempts to acquire is calculated by minimization of the total energy of the neck, taking into account the energies of bending and tilt deformations as well as the lateral tension of the neck membrane (details in Supp. Data, “Calculations of the nanotube shape”). Our analysis showed that the neck tends to either thin further or bulge, depending on the length of the detachment (Figure 6B). We found that for NT the necks shorter than the critical length (half-length, _Lc_~6.5 nm, Figure 6C) narrow, while longer necks tend to bulge out (Figure 6B). These calculations immediately suggest an explanation of why long dynamin assemblies are less effective in producing NT fission: progression of the membrane detachment for more than a couple of rungs favors bulging of the neck out of the dynamin scaffold.
The dependence of the calculated radius of the neck in its mid-point (Rmid) on the neck length is shown in Figure 6C. Rmid becomes equal to the luminal radius R0 at Lc, and attains its minimal value, Rmin, when the neck length approaches the neck diameter (i.e. when _L_~R0, Figure 6C), as expected from the general proportionality between the length and the radius of a fission neck (Fourcade et al., 1994). For NT, Rmin is less than 2 nm. Generally, when the neck diameter approaches the thickness of the lipid bilayer, conversion of a narrow membrane neck to hemi-fission intermediate is expected (Kozlovsky and Kozlov, 2003). We further analyze how the hemi-fission is achieved.
We propose that the neck transformation involve tilting of the lipids at the center of the inner monolayer of the neck. The tilting results in formation of a narrow hydrophobic “belt” leading the neck closure at the mid-point (Figure 6A). We estimated the changes in the free energy of the neck caused by the formation and expansion of such a belt for necks of different geometry (details of the calculations are described in Supp. Data, “Estimation of the possibility of the hemifission transformation for the NT”). Figure 6D shows how the calculated energy of a short (~ 9 nm) neck depends on the width (H) and radius (Rmid) of the belt. With the neck narrowing, the belt width increases reaching the monolayer thickness at the point of merger. The energy barrier along this pathway is ~ 35 kBT (Figure 6D), comparable to those reported for membrane fusion (Kuzmin et al., 2001). Thus, the merger of the inner monolayer of a neck detached from the short dynamin scaffold is energetically feasible.
Membrane rearrangements leading to merger are mainly driven by high curvature stress in the neck inner monolayer. Accordingly, the energy barrier depends sharply on the minimal radius of the thinned neck, Rmin, which should approach ~1–2 nm for the fission to occur, corroborating previous estimations (Kozlovsky and Kozlov, 2003). Formation of the hydrophobic belt becomes energetically unfavorable for even slightly wider necks (e.g. for the NT the barrier approaching 70 kBT at _Rmin_=2 nm). Rmin depends on the luminal radius (R0) of the nanotube set by the dynamin scaffold. This dependence defines a narrow range of geometrical parameters of necks where the energy barrier is less than 45 kBT (outlined by the red square, Figure 6E). For wNT (_R0_~10 nm) the neck width is always larger than 6 nm. Spontaneous fission of such thick necks is unlikely, as the corresponding energy barrier approaches hundreds of kBT. Thus, only short (~10 nm, comparable to a mean distance between the rungs of the dynamin spiral) necks progress to hemi-fission.
DISCUSSION
The pathway of membrane fission
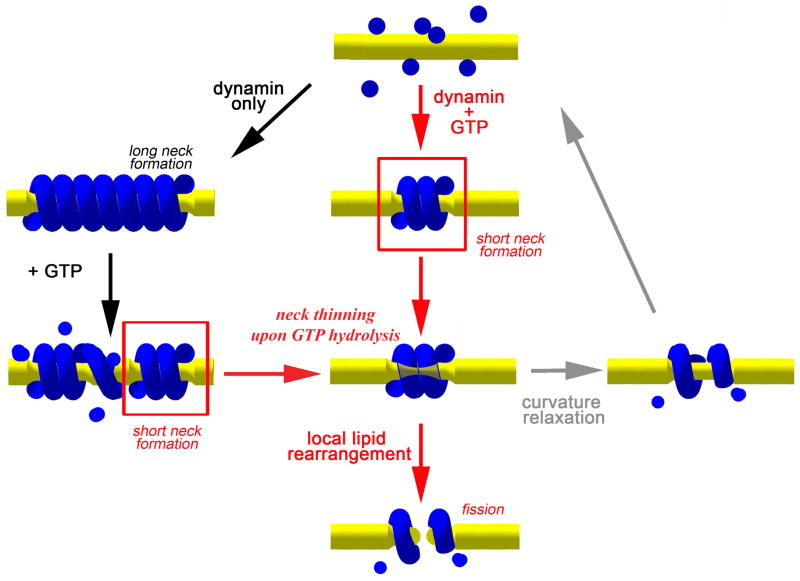
Membrane fission converges to a highly localized and fast restructuring of the lipid bilayer. Using sensitive time-resolved conductance measurements, we identified the key steps for fission of NT mediated by dynamin. Theoretical analysis of these data revealed that the fission is catalyzed in two critical steps: GTP-independent scaffolding of membrane curvature by dynamin followed by GTP-dependent disassembly of the scaffold, allowing lipid to complete membrane remodeling. This fission pathway is summarized in Figure 7. Self-assembly of dynamin scaffold induces NT narrowing until the scaffold reaches a length sufficient to trigger GTP hydrolysis. Depending on the curvature imposed to the NT, membrane detachment from the dynamin scaffold quickly following GTP hydrolysis can cause spontaneous hemi-fission followed by complete fission. This step is apparently stochastic: hemi-fission probability depends on the energy barrier for the hemi-fission transformation (Figure 6D) and on the timeframe during which the dynamin scaffold holds its rigidity upon GTP hydrolysis. On NT the scaffold softens ~10 s after the hydrolysis (Figure 5B). If fission does not happen within this time, NT expands with the softening of the scaffold and then a new squeezing cycle is initiated (Figure 7, grey arrows). Consistent with this scheme, cyclic assembly of fluorescently labeled dynamin in the presence of GTP has been visualized directly (Pucadyil and Schmid, 2008). Thus, several sequential squeezing attempts might be needed to trigger hemi-fission of the NT (Figure 4B).
Figure 7. Pathway of non-leaky membrane fission mediated by dynamin.
Dynamin polymerizes into a cylindrical scaffold: short in the presence of GTP (red arrows) and long when preassembled in the absence of GTP (black arrows). GTP hydrolysis causes detachment of the nanotube membrane from the dynamin scaffold so that fission becomes possible, but only for short membrane necks held by a dynamin scaffold. If fission is not immediate, the scaffold ultimately softens and disassembles allowing expansion of the nanotube (grey arrows). Thus, multiple rounds of assembly and disassembly of the scaffold can produce cyclic squeezing and relaxation of the nanotube.
Hemi-fission is a hypothetical transient stage in the fission pathway when the inner monolayer of a membrane neck coalesces effectively breaking the inner volume into two, while the outer monolayer remains continuous (Figure 6A). The fission of the outer monolayer completes neck scission (Kozlovsky and Kozlov, 2003). Topologically, hemi-fission is stipulated by leak-less fission, as the synchronous rupture of both monolayers inevitably yields a hole. Thus the lack of detectable membrane permeabilization (Figure 4C) strongly supports the involvement of a hemi-fission intermediate in the NT fission. Our theoretical analysis further substantiates the hemi-fission pathway demonstrating that by tight squeezing of the NT, dynamin drives merger of the inner monolayers of the NT membrane (Figure 6D).
If dynamin is pre-assembled on NT (Figure 7, black arrows), addition of GTP causes partial relaxation of the dynamin scaffold before fission occurs (Figure 5B), This relaxation likely corresponds to breaking of a long dynamin scaffold into short necks (Figure 7) identified as the most potent structures in producing NT fission by our theoretical analysis (Figure 6). Consistent with our conclusions, preassembled dynamin scaffolds are destabilized upon GTP addition and impair membrane fission, whereas a short dynamin assembly, localized to the necks of membrane buds, is sufficient to mediate membrane fission (Pucadyil and Schmid, 2008).
Membrane tubulation and fission
Dynamin tubulates lipid membranes by polymerizing into a tight cylindrical scaffold encaging the membrane (Roux et al., 2006; Praefcke and McMahon, 2004; Sweitzer and Hinshaw, 1998). This polymerization is featured as a step leading to the cooperative hydrolysis of GTP (Warnock et al., 1996; Stowell et al., 1999), hypothesized to provide most of the energy for the membrane deformations leading to fission in previous models (Warnock and Schmid, 1996; Praefcke and McMahon, 2004). However, the amount of energy that dynamin supplies to the membrane during scaffold formation had not been previously considered. We crudely estimate that ~10 kBT per dynamin molecule is consumed in tight squeezing of NT (Figure 3C), assuming complete surface membrane coverage by the dynamin spiral (Zhang and Hinshaw, 2001). This energy scale immediately suggests that dynamin is a molecule designed to bring about high curvature in a highly cooperative manner as do other membrane-tubulating proteins (Frolov and Zimmerberg, 2008). Furthermore, dynamin can produce curvature stress seemingly sufficient to cause spontaneous NT fission (Figure 2B). Then how is the energy of GTP hydrolysis used?
Our data indicate that the dynamin scaffold strongly holds the encaged NTs, likely, through membrane insertion and interactions between dynamin’s PH domain and the lipid bilayer (Ramachandran et al., 2007; Zheng et al., 1996). GTP hydrolysis quickly causes weakening of dynamin-membrane interactions followed by overall disassembly of the dynamin scaffold (Figure 5B; Ramachandran and Schmid, 2008; Pucadyil and Schmid, 2008). Thus, the energy of GTP hydrolysis is used primarily to pull the dynamin off the membrane, so that short membrane necks can further narrow and close (Figure 6A, D) and to weaken lateral interactions between dynamin molecules (Ramachandran and Schmid, 2008; Ramachandran et al., 2007; Stowell et al., 1999). It is tempting to assume that the disassembled dynamin is capable of storing the energy released upon GTP hydrolysis and membrane curvature relaxation. This energy can then be transferred back to curvature stress upon dynamin assembly into a new tight scaffold holding a membrane. This way multiple rounds of dynamin assembly provide a steady rate of GTP hydrolysis Stowell et al., 1999) directly coupled to periodic curvature creation.
Our observations argue that nanotube fission is not directly coupled to global structural rearrangements of assembled dynamin caused by GTP, generally associated with further narrowing and stressing, but not relaxation of the nanotube (Kozlov, 2001; Stowell et al., 1999; Sweitzer and Hinshaw, 1998). We can also exclude that dynamin causes some global instability of nanotube shape, e.g. pearling of the tube (Bar-Ziv Moses, 1994), which might impair the integrity of the NT membrane. Changes in the NT conductance induced by dynamin are relatively slow, ~10 s (e.g. see Figure 4B). This is substantially slower than lipid diffusion (~1s) or shape relaxation (~0.1–2s, Supp. Data) of shortened micron length NTs. Thus, short NT can adjust its shape in a quasistationary manner so that no tension gradients leading to pearling occur. Accordingly, the stress imposed by dynamin is localized to the places where the dynamin scaffolds are. In this respect, the reconstituted fission transformation is relevant to its intracellular archetype driven by short dynamin assemblies.
Despite its localized nature, dynamin-driven membrane fission is sensitive to the bulk properties of the membrane, such as lateral tension (Roux et al., 2006; Kozlov, 2001). We emphasize two main contributions of tension. First, it directly affects the curvature of a membrane cylinder as its radius is inversely proportional to tension (see Figure 1 above). Consequently, curvature stresses imposed by dynamin and tension on a cylindrical lipid nanotube sum up. Second, by increasing the mean curvature of a nanotube, tension also stimulates dynamin adsorption (Ramachandran and Schmid, 2008; Yoshida et al., 2004). Thus an increase of lateral membrane tension can stimulate fission of a cylindrical nanotube.
However, uniform squeezing of the nanotube down to radii characteristic for spontaneous fission requires particularly high lateral tensions (several dyn/cm, Supp. Figure 4) known to produce membrane leakage and rupture (e.g. Melikov et al., 2001). To minimize these complications, dynamin appears to apply membrane stress by gradual assembly of a scaffold, limited in length in the presence of GTP: dynamin does not produce a force stroke but rather a gradual and highly localized deformation sensitive to the lipid response. The membrane curvature produced by dynamin is substantially higher than those caused by relatively large lateral tension of the NT membrane (Figure 3C). Thus, the lateral tension helps but is not critical in dynamin-mediated membrane fission. We propose that in vivo accessory factors could stimulate the fission reaction externally, via augmenting lateral tension to assist dynamin in constriction and scission of a vesicle neck (Merrifield et al, 2005; Slepnev and De Camilli 2000).
Dynamin and lipids
Our experiments reveal that dynamin activity is crucially modulated by lipid composition: final diameters of dynamin-coated tubes (without GTP) are not dictated by dynamin alone, but also depend on lipid composition. If dynamin scaffold had completely dominated the energetics of tube formation, then it would have satisfied its optimal protein packing constraints by forming the same diameter tube. If, however, the energy of scaffold polymerization is comparable to the energy of membrane bending, then the final tubule diameter will depend on lipid composition. Hence, dynamin-like proteins may function as GTP-dependent curvature agents (e.g. see Pitts et al, 1999).
Since membranes bearing a high density of negatively charged PS can be tubulated without PI(4,5)P2 (Sweitzer and Hinshaw, 1998), the effect of multivalent lipid species is probably electrostatic. Our results are consistent with this view, as the PI(4,5)P2 requirement is related to the efficiency and speed of dynamin adsorption, expected to be extremely sensitive to local electrostatic interactions (Zimmerberg and McLaughlin, 2004). On highly curved NT surface, local charge density becomes less crucial, since curvature itself stimulates protein adsorption (Ramachandran and Schmid, 2008; Yoshida et al., 2004). Thus, PI(4,5)P2 enhances (Figure 3A, B), but is not essential for either the intrinsic curvature or fission activities of dynamin.
To summarize, our results reveal a tight coupling between dynamin and the lipid template. Dynamin is designed to selectively target highly curved membrane necks and probe their mechanical stability by repetitive squeezing. Fission critically depends on the geometry and mechanical parameters of the neck membrane. This dependence has a clear physiological significance: dynamin effectively cuts only those necks that are prone to fission, such as narrow necks formed at the final stages of vesicle detachment. On wider and/or more rigid necks dynamin is expected to operate as a GTP-dependent curvature regulator. Hence, cooperation of dynamin and the lipid membrane provides a universal tool to control the behavior of the neck of a vesicle.
EXPERIMENTAL PROCEDURES
Materials
Purified dynamin and dynamin conjugated to the thiol-reactive BODIPY-Fl-C1-IA probe were obtained as described (Ramachandran et al. 2007). 1,2-Dioleoyl-_sn_-Glycero-3-Phosphocholine (DOPC), 1,2-Dioleleoyl-_sn_-Glycero-3-Phospoethanolamine (DOPE), 1,2-Dioleoyl-_sn_-Glycero-3-Phospho-L-Serine (DOPS); cholesterol (Chol), Oleoyl-_sn_-Glycero-3-Phospho-L-Serine (OPS), 1,2-Dioleoyl-sn-Glycero-3-Phosphoinositol-4,5-Bisphosphate (PI(4,5)P2) and 1,2-Dioleoyl-sn-Glycero-3-Phosphoethanolamine-N-(Lissamine Rhodamine B sulfonyl) (Rh-DOPE) were from Avanti Polar Lipids (Alabaster, AL). Sodium salts of GTP, GDP, and GTPγS were from Sigma (St. Louis, MO). Buffer A contains 100 mM KCl, 10 mM HEPES pH 7.0 was used in all experiments (supplemented with 0.2 mM MgCl2 when nucleotides were used); buffer B contains sucrose and 10 mM HEPES (pH 7.0), osmotically equilibrated with Buffer A, was used for electroformation.
Phospholipid membranes
Planar phospholipid membranes were formed as described (Frolov et al., 2003b) from DOPC:DOPE:Chol:DOPS, 27.5:27.5:30:15 mol% in squalane (20 g/L, total lipid) in experiments with NT; and from DOPC:DOPE:Chol:OPS 30:30:20:20 mol% in squalane (50–100 g/L, total lipid) in experiments with wNT. Giant unilamellar vesicles (GUV) were prepared by electroformation (Angelova and Dimitrov, 1988) from DOPC:DOPE:Chol:DOPS:Rh-DOPE 30:29.5:20:15:0.5 mol/mol (for dynamin application) and POPC:DOPS:chol:RhDOPE 74.5:20:5:0.5 mol/mol (for monitoring BODIPY-dynamin adsorption) in chloroform:methanol:diethyl ether 4:1:5 vol/vol (0.1 g/L, total lipid). An electroformation chamber was mounted on the stage of the inverted fluorescence microscope (Zeiss Observer D1, 100X, 1.45NA objective lens), vesicle formation was monitored and the process stopped upon appearance of close-to-spherical vesicles, so that vesicles remained attached to the electrodes. The chamber was then perfused with buffer A.
Membrane nanotubes
Membrane nanotubes were prepared by “patch-clamping” a planar phospholipid bilayer as described (Frolov et al., 2003b, Figure 1A). The length of the nanotube was varied by micromanipulations performed by a calibrated piezo-manipulator (Newport; 30μm travel). GNT was measured at 100 mV holding potential using Axopatch 200B (Axon Instruments) or EPC-8 (HEKA Inc.) amplifiers and a PC-44 acquisition board (Signalogic); sampling frequencies f were 1 kHz and 10 kHz (for leakage measurements), signals were passed through 8-pole Bessel filters (Frequency Devices) set at _f/_2 corner frequency. Leakage measurements were performed as described (Frolov et al., 2003b).
GUVs were approached using narrow glass pipettes or carbon fibers (diameter 5 μm). Upon touching a GUV, the pipette/fiber was slowly moved away pulling the membrane nanotube. Tube formation was monitored using Olympus IX-70 inverted microscope (150X, 1.45NA objective), Cascade II camera (Photometrics), and the ImageJ-μManager software package (http://rsb.info.nih.gov/ij/). 550/590 nm excitation/emission wavelengths were used for Rh-DOPE, 505/525 nm – for BODIPY-Fl, with a halogen lamp (5–10 W) as the excitation source providing minimal photobleaching. Images were despeckled and the image background was corrected using the ImageJ software; the peak intensity of nanotube fluorescence was obtained by averaging the profiles of fluorescence intensity across the nanotube image using the Plot profile function of ImageJ.
Supplementary Material
01
02
Acknowledgments
This work was partially supported by the NIH intramural program (NICHD), and grants NIH R01GM42455 and R37.MH61345, RFBR 08-04-00085, CRDF GAP RUB1–1297(5)–MO–05, Russian Federal Agency for Science and Innovations 02.512.11.0010, and the grant for State Support of Leading Scientific Schools of Russian Federation 4181.2008.4. The BODIPY-labeled dynamin was generously provided by Rajesh Ramachandran. We are grateful to Vladimir Lizunov and Gennady Kushnir for their technical help, and Thomas Pucadyil, Anna Shnyrova and Yuri Chizmadzhev for a careful reading of the manuscript and fruitful discussions.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Allain JM, Storm C, Roux A, Ben Amar M, Joanny JF. Fission of a multiphase membrane tube. Phys Rev Lett. 2004;93:158104. doi: 10.1103/PhysRevLett.93.158104. [DOI] [PubMed] [Google Scholar]
- Angelova MI, Dimitrov DS. A mechanism of liposome electroformation. Prog Colloid Polym Sci. 1988;76:59–67. [Google Scholar]
- Bar-Ziv R, Moses E. Instability and “pearling” states produced in tubular membranes by competition of curvature and tension. Phys Rev Lett. 1994;73:1392–1395. doi: 10.1103/PhysRevLett.73.1392. [DOI] [PubMed] [Google Scholar]
- Bashkirov PV. Membrane nanotubes in the electric field as a model for measurement of mechanical parameters of the lipid bilayer. Biochemistry (Moscow) Supplement Series A: Membrane and Cell Biology. 2007;1:176–184. [Google Scholar]
- Chernomordik LV, Kozlov MM. Protein-lipid interplay in fusion and fission of biological membranes. Annu Rev Biochem. 2003;72:175–207. doi: 10.1146/annurev.biochem.72.121801.161504. [DOI] [PubMed] [Google Scholar]
- Conner SD, Schmid SL. Regulated portals of entry into the cell. Nature. 2003;422:37–44. doi: 10.1038/nature01451. [DOI] [PubMed] [Google Scholar]
- De Camilli P, Takei K, McPherson PS. The function of dynamin in endocytosis. Curr Opin Neurobiol. 1995;5:559–565. doi: 10.1016/0959-4388(95)80059-x. [DOI] [PubMed] [Google Scholar]
- Eliasson L, Proks P, Ammala C, Ashcroft FM, Bokvist K, Renstrom E, Rorsman P, Smith PA. Endocytosis of secretory granules in mouse pancreatic beta-cells evoked by transient elevation of cytosolic calcium. J Physiol. 1996;493(Pt 3):755–767. doi: 10.1113/jphysiol.1996.sp021420. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Evans E, Yeung A. Hidden dynamics in rapid changes of bilayer shape. Chem Phys Lipids. 1994;73:39–56. [Google Scholar]
- Fourcade B, Miao L, Rao M, Wortis M, Zia RK. Scaling analysis of narrow necks in curvature models of fluid lipid-bilayer vesicles. Phys Rev E Stat Phys Plasmas Fluids Relat Interdiscip Topics. 1994;49:5276–5286. doi: 10.1103/physreve.49.5276. [DOI] [PubMed] [Google Scholar]
- Frolov VA, Dunina-Barkovskaya AY, Samsonov AV, Zimmerberg J. Membrane permeability changes at early stages of influenza hemagglutinin-mediated fusion. Biophys J. 2003a;85:1725–1733. doi: 10.1016/S0006-3495(03)74602-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frolov VA, Lizunov VA, Dunina-Barkovskaya AY, Samsonov AV, Zimmerberg J. Shape bistability of a membrane neck: a toggle switch to control vesicle content release. Proc Natl Acad Sci U S A. 2003b;100:8698–8703. doi: 10.1073/pnas.1432962100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frolov VA, Zimmerberg J. Flexible scaffolding made of rigid BARs. Cell. 2008;132:727–729. doi: 10.1016/j.cell.2008.02.025. [DOI] [PubMed] [Google Scholar]
- Gallop JL, Jao CC, Kent HM, Butler PJ, Evans PR, Langen R, McMahon HT. Mechanism of endophilin N-BAR domain-mediated membrane curvature. EMBO J. 2006;25:2898–2910. doi: 10.1038/sj.emboj.7601174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Henriksen J, Rowat AC, Ipsen JH. Vesicle fluctuation analysis of the effects of sterols on membrane bending rigidity. Eur Biophys J. 2004;33:732–741. doi: 10.1007/s00249-004-0420-5. [DOI] [PubMed] [Google Scholar]
- Hinshaw JE. Dynamin and its role in membrane fission. Annu Rev Cell Dev Biol. 2000;16:483–519. doi: 10.1146/annurev.cellbio.16.1.483. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hinshaw JE, Schmid SL. Dynamin self-assembles into rings suggesting a mechanism for coated vesicle budding. Nature. 1995;374:190–192. doi: 10.1038/374190a0. [DOI] [PubMed] [Google Scholar]
- Jan Bukman D, Hua Yao J, Wortis M. Stability of cylindrical vesicles under axial tension. Phys Rev E Stat Phys Plasmas Fluids Relat Interdiscip Topics. 1996;54:5463–5468. doi: 10.1103/physreve.54.5463. [DOI] [PubMed] [Google Scholar]
- Kozlov MM. Fission of biological membranes: interplay between dynamin and lipids. Traffic. 2001;2:51–65. doi: 10.1034/j.1600-0854.2001.020107.x. [DOI] [PubMed] [Google Scholar]
- Kozlovsky Y, Kozlov MM. Membrane fission: model for intermediate structures. Biophys J. 2003;85:85–96. doi: 10.1016/S0006-3495(03)74457-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuzmin PI, Zimmerberg J, Chizmadzhev YA, Cohen FS. A quantitative model for membrane fusion based on low-energy intermediates. Proc Natl Acad Sci U S A. 2001;98:7235–7240. doi: 10.1073/pnas.121191898. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marks B, Stowell MH, Vallis Y, Mills IG, Gibson A, Hopkins CR, McMahon HT. GTPase activity of dynamin and resulting conformation change are essential for endocytosis. Nature. 2001;410:231–235. doi: 10.1038/35065645. [DOI] [PubMed] [Google Scholar]
- Merrifield CJ, Perrais D, Zenisek D. Coupling between clathrin-coated-pit invagination, cortactin recruitment, and membrane scission observed in live cells. Cell. 2005;121:593–606. doi: 10.1016/j.cell.2005.03.015. [DOI] [PubMed] [Google Scholar]
- Pitts KR, Yoon Y, Krueger EW, McNiven MA. The dynamin-like protein DLP1 is essential for normal distribution and morphology of the endoplasmic reticulum and mitochondria in mammalian cells. Mol Biol Cell. 1999;10:4403–4417. doi: 10.1091/mbc.10.12.4403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Praefcke GJ, McMahon HT. The dynamin superfamily: universal membrane tubulation and fission molecules? Nat Rev Mol Cell Biol. 2004;5:133–147. doi: 10.1038/nrm1313. [DOI] [PubMed] [Google Scholar]
- Ramachandran R, Schmid SL. Real-time detection reveals that effectors couple dynamin’s GTP-dependent conformational changes to the membrane. EMBO J. 2008;27:27–37. doi: 10.1038/sj.emboj.7601961. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramachandran R, Surka M, Chappie JS, Fowler DM, Foss TR, Song BD, Schmid SL. The dynamin middle domain is critical for tetramerization and higher-order self-assembly. EMBO J. 2007;26:559–566. doi: 10.1038/sj.emboj.7601491. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rappoport JZ, Heyman KP, Kemal S, Simon SM. Dynamics of dynamin during clathrin mediated endocytosis in PC12 cells. PLoS ONE. 2008;3:e2416. doi: 10.1371/journal.pone.0002416. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosenboom H, Lindau M. Exo-endocytosis and closing of the fission pore during endocytosis in single pituitary nerve terminals internally perfused with high calcium concentrations. Proc Natl Acad Sci U S A. 1994;91:5267–5271. doi: 10.1073/pnas.91.12.5267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roux A, Uyhazi K, Frost A, De Camilli P. GTP-dependent twisting of dynamin implicates constriction and tension in membrane fission. Nature. 2006;441:528–531. doi: 10.1038/nature04718. [DOI] [PubMed] [Google Scholar]
- Slepnev VI, De Camilli P. Accessory factors in clathrin-dependent synaptic vesicle endocytosis. Nat Rev Neurosci. 2000;1:161–172. doi: 10.1038/35044540. [DOI] [PubMed] [Google Scholar]
- Stowell MH, Marks B, Wigge P, McMahon HT. Nucleotide-dependent conformational changes in dynamin: evidence for a mechanochemical molecular spring. Nat Cell Biol. 1999;1:27–32. doi: 10.1038/8997. [DOI] [PubMed] [Google Scholar]
- Suss-Toby E, Zimmerberg J, Ward GE. Toxoplasma invasion: the parasitophorous vacuole is formed from host cell plasma membrane and pinches off via a fission pore. Proc Natl Acad Sci U S A. 1996;93:8413–8418. doi: 10.1073/pnas.93.16.8413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sweitzer SM, Hinshaw JE. Dynamin undergoes a GTP-dependent conformational change causing vesiculation. Cell. 1998;93:1021–1029. doi: 10.1016/s0092-8674(00)81207-6. [DOI] [PubMed] [Google Scholar]
- Takei K, McPherson PS, Schmid SL, De Camilli P. Tubular membrane invaginations coated by dynamin rings are induced by GTP-gamma S in nerve terminals. Nature. 1995;374:186–190. doi: 10.1038/374186a0. [DOI] [PubMed] [Google Scholar]
- Warnock DE, Hinshaw JE, Schmid SL. Dynamin self-assembly stimulates its GTPase activity. J Biol Chem. 1996;271:22310–22314. doi: 10.1074/jbc.271.37.22310. [DOI] [PubMed] [Google Scholar]
- Warnock DE, Schmid SL. Dynamin GTPase, a force-generating molecular switch. Bioessays. 1996;18:885–893. doi: 10.1002/bies.950181107. [DOI] [PubMed] [Google Scholar]
- Yoshida Y, Kinuta M, Abe T, Liang S, Araki K, Cremona O, Di Paolo G, Moriyama Y, Yasuda T, De Camilli P, Takei K. The stimulatory action of amphiphysin on dynamin function is dependent on lipid bilayer curvature. EMBO J. 2004;23:3483–3491. doi: 10.1038/sj.emboj.7600355. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang P, Hinshaw JE. Three-dimensional reconstruction of dynamin in the constricted state. Nat Cell Biol. 2001;3:922–926. doi: 10.1038/ncb1001-922. [DOI] [PubMed] [Google Scholar]
- Zheng J, Cahill SM, Lemmon MA, Fushman D, Schlessinger J, Cowburn D. Identification of the binding site for acidic phospholipids on the pH domain of dynamin: implications for stimulation of GTPase activity. J Mol Biol. 1996;255:14–21. doi: 10.1006/jmbi.1996.0002. [DOI] [PubMed] [Google Scholar]
- Zimmerberg J, McLaughlin S. Membrane curvature: how BAR domains bend bilayers. Curr Biol. 2004;14:R250–252. doi: 10.1016/j.cub.2004.02.060. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
01
02