Using deep sequencing to characterize the biophysical mechanism of a transcriptional regulatory sequence (original) (raw)
Abstract
Cells use protein-DNA and protein-protein interactions to regulate transcription. A biophysical understanding of this process has, however, been limited by the lack of methods for quantitatively characterizing the interactions that occur at specific promoters and enhancers in living cells. Here we show how such biophysical information can be revealed by a simple experiment in which a library of partially mutated regulatory sequences are partitioned according to their in vivo transcriptional activities and then sequenced en masse. Computational analysis of the sequence data produced by this experiment can provide precise quantitative information about how the regulatory proteins at a specific arrangement of binding sites work together to regulate transcription. This ability to reliably extract precise information about regulatory biophysics in the face of experimental noise is made possible by a recently identified relationship between likelihood and mutual information. Applying our experimental and computational techniques to the Escherichia coli lac promoter, we demonstrate the ability to identify regulatory protein binding sites de novo, determine the sequence-dependent binding energy of the proteins that bind these sites, and, importantly, measure the in vivo interaction energy between RNA polymerase and a DNA-bound transcription factor. Our approach provides a generally applicable method for characterizing the biophysical basis of transcriptional regulation by a specified regulatory sequence. The principles of our method can also be applied to a wide range of other problems in molecular biology.
Keywords: gene regulation, lac promoter, mutual information, thermodynamic models, parallel tempering Monte Carlo
Cells regulate transcription primarily through the binding of proteins to DNA-binding sites within transcriptional regulatory sequences (TRSs). Understanding how TRSs use different arrangements of binding sites to encode regulatory programs remains a major challenge for molecular biology. High-throughput methods have spurred great progress in cataloging the genome-wide distribution of binding sites (1 and 2), and many techniques exist for characterizing the sequence specificity of individual regulatory proteins (3–6). However, determining how a specific TRS integrates information from multiple DNA-bound proteins still requires a laborious series of biochemical experiments that typically provide only qualitative information (reviewed in ref. 7).
The E. coli lac promoter (8 and 9) is one of the few TRSs whose function is well understood at the biophysical level (10 and 11). Kuhlman et al. (11) were the first to prove that a certain aspect of this system—the up-regulation of transcription by the protein CRP (12)—could be quantitatively explained by a simple energetic interaction between CRP and the _σ_70-dependent RNA polymerase holoenzyme (henceforth RNAP). To do this, Kuhlman et al. measured transcriptional activity resulting from different in vivo concentrations of active CRP and showed that the resulting functional form of this activity was consistent with a simple thermodynamic model (13). By fitting the defining parameters of this model to their data, Kuhlman et al. were then able to measure the in vivo interaction energy between CRP and RNAP.
Despite its success, Kuhlman et al.’s approach is not feasible as a general method for studying TRSs. First, it requires quantitative control over the in vivo concentrations of all of the proteins that bind the TRS of interest. Secondly, TRSs typically contain multiple binding sites for each operative regulatory protein, making it difficult to determine the specific role of each site simply by varying the concentration of the regulator. This latter fact has created difficulty for similar studies of eukaryotic enhancers (14).
We hypothesized that measuring the activities of a large number of TRSs containing scattered point mutations could provide information similar to that produced by Kuhlman et al.’s method. This approach would be feasible for studying arbitrary TRSs, and would allow the effect of each individual binding site to be characterized. Because point mutations tend to preserve the spatial arrangement of binding sites, such measurements would allow one to interrogate the same protein-DNA complexes that allow the wild-type TRS to function. A similar approach had been tried by Schneider and Stormo in 1989 (15), but the recent advent of ultra-high-throughput sequencing, together with new techniques in machine learning (16) led us to believe that this approach could be much more powerful than had previously been realized.
In this article we report the application of this mutagenesis-based approach to the E. coli lac promoter. FACS (17) and 454 pyrosequencing (18) were used to characterize the activities of ∼200,000 lac promoters mutagenized in a 75 bp region containing the CRP and RNAP binding sites (Fig. 1A). The resulting sequence data allowed us to identify these binding sites de novo, determine the sequence-dependent binding energy of both CRP and RNAP, and measure the in vivo interaction energy between these two proteins in their native DNA-bound configuration. We note that previous attempts to determine in vivo protein-protein interaction energies from sequence data (19 and 20) required unproven assumptions about how arbitrary arrangements of DNA-bound proteins interact; our approach does not.
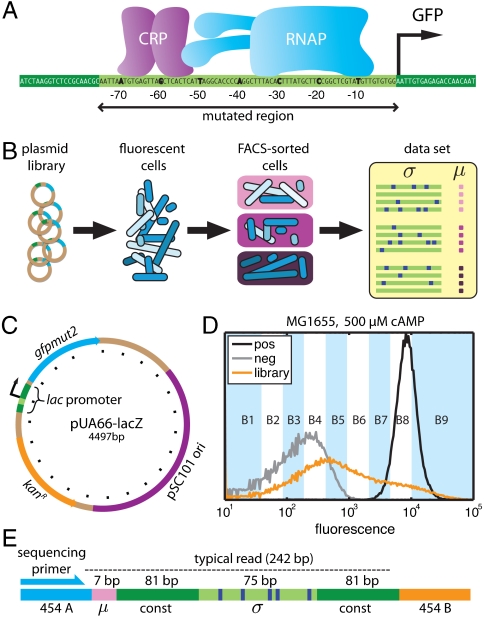
Fig. 1.
Overview of the experiments. A) We used lac promoters mutagenized in region [-75∶-1] to drive the expression of GFP. B) Plasmids containing mutant lac promoters driving GFP expression were transformed into E. coli. Induced cells were then partitioned using FACS. Deep sequencing of the mutant promoters in each FACS batch yielded a long list of sequences σ with corresponding measurements μ. C) Plasmid pUA66-lacZ (21), a very-low-copy-number plasmid on which the wild-type lac promoter drives the expression of GFP; tick mark spacing is 200 bp. D) Fluorescence distributions of MG1655 cells containing the full-wt plasmid library (orange), the pUA66-lacZ plasmid (black), or a negative control plasmid pJK10 (SI Appendix: Fig. S1) in which region [-75∶-1] of the lac promoter was deleted (gray). In the full-wt experiment, batches B1–B9 received cells from the indicated fluorescence ranges, while batch B0 received cells randomly sampled from the initial library. E) Each PCR amplicon contained a 7 bp DNA barcode indicating the batch μ in which the sequence σ was found. 454 pyrosequencing (18) yielded reads of about 242 bp covering the indicated regions.
In this way, we demonstrate how deep sequencing can be used to measure protein-DNA and protein-protein interaction energies in living cells. This ability should be useful for addressing many different questions in molecular biology.
Interrogating a TRS with Flow Cytometry and Deep Sequencing
We performed six experiments on region [-75∶-1] of the E. coli lac promoter (Fig. 1 A and B). These experiments, summarized in Table 1, differed in the positions within region [-75∶-1] that were mutagenized, the strain of E. coli used, and the physiological conditions under which lac promoter function was characterized.
Table 1.
Shown for each of our six experiments are the mutagenized region of the lac promoter, the per-position substitution rate, the E. coli strain used, the cAMP concentration used for induction, the number of batches into which cells were sorted, and the final number of filtered, nonredundant reads
| Dataset | Mut. region | Mut. rate | Strain | cAMP (μM) | No. μ | No. reads |
|---|---|---|---|---|---|---|
| full-wt | [-75∶-1] | 12% | MG1655 | 500 | 10 | 51,835 |
| crp-wt | [-74∶-49] | 24% | MG1655 | 500 | 10 | 46,986 |
| rnap-wt | [-39∶-4] | 15% | MG1655 | 500 | 10 | 45,461 |
| full-500 | [-75∶-1] | 12% | TK310 | 500 | 5 | 23,431 |
| full-150 | [-75∶-1] | 12% | TK310 | 150 | 5 | 24,334 |
| full-0 | [-75∶-1] | 12% | TK310 | 0 | 5 | 28,544 |
The full-wt experiment used a library of reporter constructs, derived from pUA66-lacZ (Fig. 1C; ref. 21), in which region [-75∶-1] of the lac promoter was mutagenized at 12% per nucleotide, yielding 9 ± 3 substitution mutations per sequence. Wild-type E. coli (strain MG1655) were transformed with this plasmid library, after which GFP expression was induced during exponential growth in minimal media supplemented with glucose, cAMP, and 1 mM isopropyl β-D-1-thiogalactopyranoside (IPTG). FACS (17) was used to sort induced cells into 10 different batches, each cell according to its measured fluorescence (Fig. 1D). PCR was then used to tag mutant TRSs according to the batch in which each TRS was found (Fig. 1E). 454 pyrosequencing (18) of the resulting PCR amplicons yielded a list of 51,835 mutant TRSs and corresponding batches. The batch μ associated with each TRS σ serves as a noisy and qualitative measurement of that TRS’s in vivo transcriptional activity. Experiments crp-wt and rnap-wt were performed the same way, but using mutant TRSs in which only the CRP or RNAP binding site was mutagenized (Table 1).
The full-500, full-150, and full-0 experiments were performed using the same plasmid library as in full-wt, but with transcriptional activity assayed in E. coli strain TK310 (11) grown in 500 μM, 150 μM, or 0 μM cAMP, respectively. Cells were also sorted into five batches instead of 10. Strain TK310 lacks adenlyate cyclase (cyaA, needed for cAMP synthesis) and phosphodiesterase (cpdA, which degrades cAMP) and is therefore unable to control its intracellular cAMP levels (11). Growing TK310 cells in media supplemented with different concentrations of cAMP thus allowed us to control the active intracellular concentration of CRP (just as Kuhlman et al. did). Importantly, though, the mechanism of lac promoter function is the same in both MG1655 and TK310 cells.
In total we obtained 220,591 mutant TRSs, with each TRS σ assigned a noisy, qualitative measurement μ of its transcriptional activity (Fig. 1B). These sequences σ and measurements μ comprise the only data used in the analysis that follows.
Information Footprints Reveal Functional Binding Sites
Our first goal was to identify nucleotide positions that affect expression, thereby locating all functional binding sites within the probed region of the lac promoter. For this purpose we used mutual information, a fundamental quantity from information theory that provides the most general measure of dependence between any two variables (22). For each nucleotide position i, we computed the number of sequences in each batch μ having each of the four possible bases b i. We then used this information to compute the mutual information I(b i; μ) between b i and μ (see SI Appendix: Computing mutual information for details), thereby quantifying the effect of the base at position i on our measurements. Plotting the mutual information I(b i; μ) for each position i produced what we call an “information footprint.”
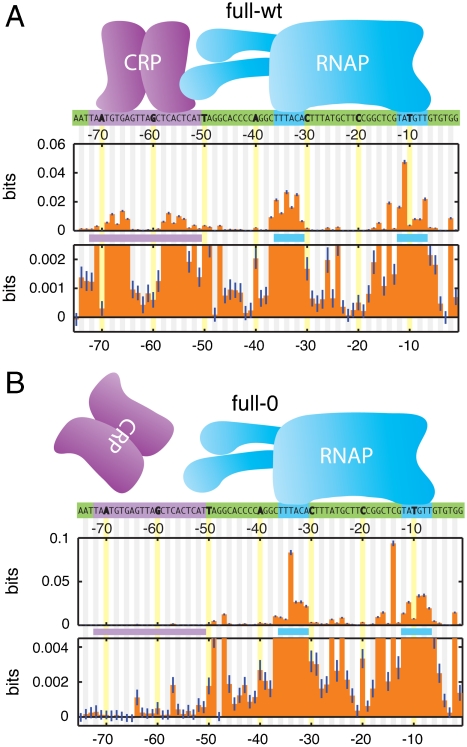
Fig. 2A shows the information footprint produced by the full-wt experiment. The known binding sites of CRP and RNAP are clearly visible and each has the expected bipartite structure: CRP binds DNA as a homodimer at [-72∶-51] with a 6 bp gap between its two DNA-binding domains, while RNAP binding to [-41∶-1] results from the recognition of separate sequence elements centered roughly on positions -10 and -35 (8 and 12).
Fig. 2.
Information footprints. A) Footprint from full-wt data, aligned with known protein-DNA contact positions (highlighted). The lower plot is a 20X magnification of the upper plot. Error bars (dark blue lines) indicate uncertainties due to finite sample effects (SI Appendix: Computing mutual information). B) Footprint from the full-0 experiment, in which intracellular CRP was inactive. SI Appendix: Fig. S3 shows information footprints from all six experiments.
The information values displayed in Fig. 2A are small, ranging from ∼0.05 bits down to values indistinguishable from zero. This is not surprising, since each I(b i; μ) measures the effect on transcription of just one out of 75 positions. But because our dataset is large (N = 51,856), these information values are determined very precisely—typically to within ∼4 × 10-4 bits. Fig. 2A thus displays meaningful information values ranging over two orders of magnitude. This high level of sensitivity can reveal aspects of sequence function not detectable by other methods, e.g., (23). For instance, small but significant effects on expression were observed between the -10 and -35 elements and between the CRP and RNAP sites, regions not previously thought to influence transcription at the lac promoter. Indeed, only the 10 positions [-75,-70,-48,-42,-41,-23,-22,-21,-19,-3] show an insignificant effect on expression (i.e., P > 0.05).
Information footprints can further allow one to determine which of the identified sites are involved in the response to a specific biochemical signal or genetic perturbation. Fig. 2B shows the information footprint from the full-0 experiment, in which TK310 cells were induced in the absence of cAMP, thereby inactivating intracellular CRP. The lack of active CRP is reflected in the near-total loss of information at positions [-75∶-51]: information values at all but three positions within this 25 bp site differ insignificantly from zero (i.e., P > 0.05). An intermediate reduction in information occurs in the full-150 footprint, while the full-500 footprint closely resembles that of full-wt (SI Appendix: Fig. S3). We note that the small but significant information values at positions [-64,-57,-52] in the full-0 footprint might result from interactions between DNA and the α subunits of RNAP (24), or from alternative RNAP binding sites (25).
An important caveat to this analysis is that the quantitative features of an information footprint ultimately depend on the details of one’s experiment, including the level of mutagenesis used in the initial TRS library and the specific fluorescence gates used for sorting cells. So while qualitative differences between footprints from different experiments can be revealing, it is difficult to draw conclusions from more subtle quantitative differences, such as the different shapes of the RNAP footprint in Fig. 2 A and B. But as we show in the next section, explicit biophysical models can be fit to data in a way that does not depend on such experimental details. Quantitative differences between models inferred from different experiments can, as a result, be revealing about underlying molecular mechanisms.
Model Fitting in the Presence of Uncharacterized Noise
Next we used our data to infer quantitative models for how in vivo protein-DNA and protein-protein interactions modulate transcription. By “model” we mean a mathematical function that assigns to each sequence σ a predicted value x for some quantity of interest, such as the DNA-binding energy of a regulatory protein, or the rate of transcription resulting from the interactions between multiple proteins. To infer a given model, we first assumed a specific mathematical formula for the model, then determined the values of model parameters by matching the sequence-dependent predictions x to our sequence-specific measurements μ.
Such model fitting could be done in the standard Bayesian way if we knew the experimental “error model” p(μ|x)—the probability of obtaining a measurement μ given an underlying quantity of interest x (such as binding energy or transcription rate). But in our experiments it was virtually impossible to accurately determine p(μ|x) a priori. Many difficult-to-characterize noise processes, including stochastic transcription, variations in cell size, and noise in FACS measurements, contribute to the quantitative form of p(μ|x). Also, in the case where x represents the DNA-binding energy of a protein, we do not know a priori how the binding of that protein affects transcription; indeed, this is something we want to learn from the data. Kinney et al. (16) overcame this problem by computing likelihood in the presence of an explicitly uncertain error model. They showed that regardless of what p(μ|x) actually is, the likelihood of a candidate model is well approximated by
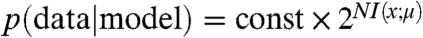 |
[1] |
|---|
in the limit where the number N of independently measured sequences is sufficiently large. Here I(x; μ) is the “predictive information” of the model—the mutual information between model predictions x and measurements μ. Although Kinney et al. focused on the analysis of microarray data, Eq. 1 is applicable to any dataset consisting of a large number of sequences and corresponding measurements. Kinney et al.’s approach therefore provides a practical substitute for standard likelihood-based inference when the experimental error model is either difficult to characterize or is unknowable a priori (see SI Appendix: Statistical inference using mutual information for more discussion).
In the analysis that follows, we used a custom parallel tempering Monte Carlo algorithm to sample model parameters according to the right-hand-side of Eq. 1 (see SI Appendix: Parallel tempering Monte Carlo sampling of model parameters). This allowed us to determine not just the best values for model parameters, i.e., which values maximize predictive information I(x; μ), but also the uncertainty in each parameter due to finite data. Because N > 104 for all of the experiments described in this article, even changes as small as 10-4 bits in the value of I(x; μ) led to substantial changes in model likelihood. The large amount of data produced by our experiments thus allowed us to determine precise quantitative values for model parameters even though our measurements were noisy and qualitative.
in Vivo Interaction Energies from Sequence Data
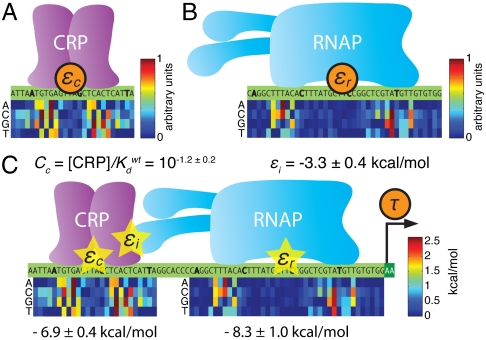
Having located the binding sites of both CRP and RNAP de novo using information footprints, we sought an explicit model for each protein’s sequence-dependent binding energy. For this we used “energy matrix” models: each base within a protein’s binding site was assumed to contribute additively to the overall binding energy. These simple models have been shown to accurately describe a number of transcription factors, (e.g., refs. 26 and 27), though there are known exceptions (28 and 29).
We fit an energy matrix for CRP to positions [-74∶-49] using the full-wt dataset. Energy matrix elements were sampled, according to Eq. 1, using the predictive information I(ε c; μ) where ε c is CRP’s predicted binding energy. The resulting optimal matrix is shown in Fig. 3A. We similarly fit an energy matrix to positions [-41∶-1] to model RNAP’s binding energy ε r (Fig. 3B). CRP and RNAP energy matrices were also inferred from our five other datasets (SI Appendix: Fig. S4 A). We note that at this stage of our analysis we were able to determine each matrix only up to an unknown multiplicative constant, not in physical units such as kcal/mol (see SI Appendix: Maximizing mutual information leaves some model parameters undetermined).
Fig. 3.
Models fit to full-wt data. A) The CRP energy matrix fit to [-75∶-49] by maximizing I(ε c; μ) on full-wt data. B) The RNAP energy matrix fit to [-41∶-1] by maximizing I(ε r; μ) on full-wt data. In A and B, each matrix column lists the energy contributions of the four possible bases at the aligned position within the site. Matrix elements range from 0 to 1 (in arbitrary units) with the lowest element in each column set to zero by convention. SI Appendix: Fig. S4 shows the CRP and RNAP matrices derived from all six of our datasets. C) The thermodynamic model for τ inferred using I(τ; μ) in Eq. 1. Optimal CRP and RNAP energy matrices are shown with elements expressed in kcal/mol (1 kcal/mol = 1.62_k_ b T at T = 310 °K). It is useful to define each wild-type lac promoter site as having zero energy. We therefore add an energy shift, shown below each matrix, when computing ε c and ε r. Doing this means that C c represents the intracellular CRP concentration in units of the dissociation constant of the wild-type (zero energy) site. Values quoted for ε i and C c are mean ± rmsd values determined from the parameter ensembles sampled using parallel tempering Monte Carlo.
Unlike information footprints, these energy matrices are meant to capture intrinsic properties of the regulatory proteins, properties that should not depend on specific ways cells were sorted or on the level of mutagenesis used in the TRS library. The optimal matrices inferred from our six experiments (4 matrices for CRP, 5 for RNAP) are nearly identical, supporting this interpretation: CRP matrix elements derived from different experiments correlate by > 95% (SI Appendix: Fig. S4 B), while RNAP matrix elements exhibit > 92% correlation (SI Appendix: Fig. S4C). Furthermore, each of these matrix models performs better on every one of our datasets than do any of the models for either CRP or RNAP currently in the literature (with two minor exceptions; see SI Appendix: Model comparison to literature). We find this level of quantitative agreement between experiments remarkable, considering that our six experiments used different promoter libraries, different E. coli strains (MG1655 or TK310), different inducing conditions (500 μM, 150 μM, or 0 μM cAMP), and different fluorescence gates for sorting cells. This close agreement in the face of important experimental differences attests to both the usefulness and correctness of Eq. 1.
Our inferred CRP and RNAP energy matrices recapitulate much of what is known about the sequence specificities of these two proteins. The known consensus sequences—TGTGA(N)6TCACA for CRP (3) and TTGACA(N)18TATAAT for RNAP (30)—exactly match the lowest energy sequences predicted by nearly every one of our matrix models. The one exception is the RNAP matrix fit to full-0 data, which predicts that TTGATA will have slightly lower energy than TTGACA in the -35 region. We note that every one of our RNAP matrices also predicts that having a “G” at position [-14] increases RNAP binding strength. In the literature this G is said to create an “extended -10 promoter,” and such promoters are known to have increased transcriptional activity. Our CRP matrices are also in qualitative agreement with previous in vitro measurements (31), though there are some quantitative discrepancies.
Next we sought a quantitative understanding of how the interaction of CRP with RNAP affects transcription. Kuhlman et al. (11) previously showed that a simple biophysical model based on equilibrium statistical mechanics (reviewed in ref. 13) accounted well for the effect of cAMP on lacZ expression in TK310 cells. We hypothesized that using energy matrices to describe the binding energies of CRP and RNAP within Kuhlman et al.’s model, then fitting all model parameters to our data de novo, would allow us to recover Kuhlman et al.’s results, including their measurement of the interaction energy between CRP and RNAP.
Following Kuhlman et al., we assumed that the rate of transcription τ at the lac promoter is proportional to the occupancy of RNAP at its binding site in thermal equilibrium. This model is quantitatively expressed as
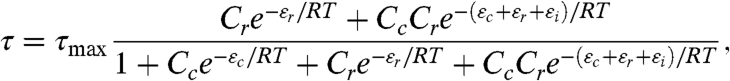 |
[2] |
|---|
where RNAP occupancy is given by the sum of Boltzmann weights corresponding to physical states in which RNAP is bound, divided by the sum of weights for all possible states of the system. These Boltzmann weights depend on (i) the CRP and RNAP binding energies ε c and ε r, which we express in kcal/mol and normalize to be zero at each wild-type lac promoter site, (ii) the concentrations C c and C r of CRP and RNAP, expressed in units of each wild-type site’s dissociation constant and (iii) the CRP-RNAP interaction energy ε i, expressed in kcal/mol. _τ_max is the transcription rate resulting from full RNAP occupancy. R = 1.98 × 10-3 kcal/mol °K is the gas constant and T = 310 °K (37 °C) is the temperature at which cells were induced.
Using I(τ; μ) evaluated on full-wt data, we fit all of the parameters defining τ, including ε i, C c, and the elements of the energy matrices used to compute ε c and ε r. Doing so we inferred a CRP-RNAP interaction energy ε i = -3.26 ± 0.41 kcal/mol. This value is consistent with Kuhlman et al.’s measurement of -3.4 kcal/mol (11), thus demonstrating that DNA sequence data can be used to measure the in vivo interaction energy between two proteins. This procedure also yielded an in vivo CRP concentration of 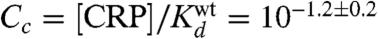 . Fig. 3C shows these values for ε i and C c, as well as the optimal energy matrices for ε c and ε r inferred by fitting τ. These matrices closely resemble those in Fig. 3 A and B, but, unlike the matrices we inferred by separately fitting ε c and ε r, their elements are determined explicitly in physical units of kcal/mol. We note that fitting τ to full-wt data provided no information about the value of either _τ_max or C r (see SI Appendix: Maximizing mutual information leaves some model parameters undetermined).
. Fig. 3C shows these values for ε i and C c, as well as the optimal energy matrices for ε c and ε r inferred by fitting τ. These matrices closely resemble those in Fig. 3 A and B, but, unlike the matrices we inferred by separately fitting ε c and ε r, their elements are determined explicitly in physical units of kcal/mol. We note that fitting τ to full-wt data provided no information about the value of either _τ_max or C r (see SI Appendix: Maximizing mutual information leaves some model parameters undetermined).
Testing Biochemical Mechanisms by Fitting a Single Model to Multiple Datasets
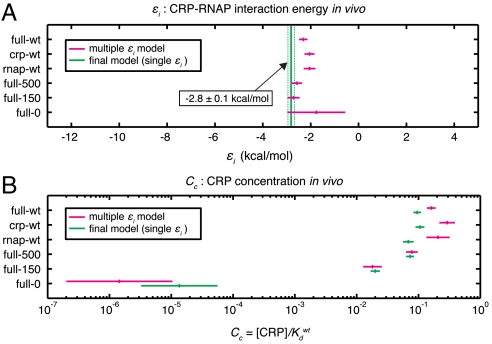
cAMP is known to alter lac promoter activity by affecting CRP’s ability to bind DNA, not CRP’s interaction with RNAP. Both of these possibilities, though, are consistent with the information footprints shown in Fig. 2. By contrast, the former hypothesis predicts that the CRP concentration C c in our model for τ should vary from experiment to experiment, while the latter predicts an experiment-dependent interaction energy ε i. To further test the validity of our approach, we fit a single model for τ to all six of our datasets (see SI Appendix: Fitting a model to multiple data sets). This multidataset model employed a single CRP energy matrix and a single RNAP energy matrix, but allowed for dataset-specific values for both ε i and C c.
The experiment-specific values we inferred for ε i and C c are shown in Fig. 4 A and B. The ε i values determined for all six experiments are mutually consistent (P > 0.05, _χ_2 test), whereas the six C c values differ very significantly: C c values for experiments full-0 and full-150, which were performed in reduced concentrations of cAMP, were found to be much lower than the C c values determined for the other four experiments. These results verify the well known fact that cAMP affects the concentration of active CRP, not the strength of CRP’s interaction with RNAP (8 and 12).
Fig. 4.
Parameters fit to all six datasets. A) CRP-RNAP interaction energies ε i (mean ± rmsd) inferred by fitting τ to all six datasets, using either data-set-specific values for ε i (magenta) or a single ε i for all six datasets (green). B) CRP concentrations C c inferred for these same multidataset models. SI Appendix: Fig. S5 shows full ensemble distributions for ε i and the six C c parameters of the final model, together with mean and rmsd values for all the CRP and RNAP matrix elements.
Repeating this inference using only one ε i value for all six experiments yielded the final inferred model of this article (Fig. 4 and SI Appendix: Fig. S5). The CRP-RNAP interaction energy inferred from all six datasets is ε i = -2.82 ± 0.13 kcal/mol. This differs from Kuhlman et al.’s measurement, but only by ∼20%. Also, the ratio of CRP concentrations inferred for full-150 and full-500 (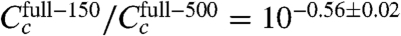 ) closely agrees with the ratio of cAMP (150 μM/500 μM = 10-0.52) used in these two experiments. This agreement is consistent with Kuhlman et al.’s observation that, for TK310 cells, the concentration of active CRP in vivo is proportional to the exogenous concentration of cAMP (11). Indeed, even the expected trace amount of cAMP present in the full-0 induction media (∼50 nM, a result of carry-over from the starter culture inoculum) is fully consistent with the much reduced yet significantly nonzero value for
) closely agrees with the ratio of cAMP (150 μM/500 μM = 10-0.52) used in these two experiments. This agreement is consistent with Kuhlman et al.’s observation that, for TK310 cells, the concentration of active CRP in vivo is proportional to the exogenous concentration of cAMP (11). Indeed, even the expected trace amount of cAMP present in the full-0 induction media (∼50 nM, a result of carry-over from the starter culture inoculum) is fully consistent with the much reduced yet significantly nonzero value for 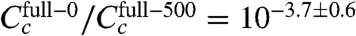 .
.
We note, however, that there are also puzzling quantitative oddities in our results. Our CRP concentration ratios are in good agreement with expectations, but the absolute values we inferred (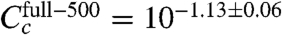 and
and 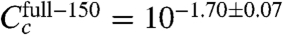 ) are about 20-fold lower than the corresponding values claimed by Kuhlman et al. (SI Appendix: Model comparison to literature). Also, in the six-ε i fit, the average ε i is -2.34 ± 0.09 kcal/mol, substantially less than the -2.82 ± 0.13 kcal/mol we inferred using a common ε i for all six experiments. Finally, all of our inferred CRP energy matrices are asymmetric and predict that CRP binds in the energetically unfavorable orientation at the wild-type CRP site. We think these strange results probably result from our models for ε c, ε r, and τ being too simplistic. The issue of model selection is complicated, however, and is beyond the scope of this article.
) are about 20-fold lower than the corresponding values claimed by Kuhlman et al. (SI Appendix: Model comparison to literature). Also, in the six-ε i fit, the average ε i is -2.34 ± 0.09 kcal/mol, substantially less than the -2.82 ± 0.13 kcal/mol we inferred using a common ε i for all six experiments. Finally, all of our inferred CRP energy matrices are asymmetric and predict that CRP binds in the energetically unfavorable orientation at the wild-type CRP site. We think these strange results probably result from our models for ε c, ε r, and τ being too simplistic. The issue of model selection is complicated, however, and is beyond the scope of this article.
Model Validation Using Predictive Information
Predictive information can be used to determine how well a proposed thermodynamic model integrates binding energies into a single transcriptional output. The predictive information I(τ; μ) quantifies how well the biophysical model in Eq. 2 accounts for our measurements μ. However, we can also directly compute the predictive information I(ε c,ε r; μ) of the pair of binding energies, ε c and ε r, without any model for τ (SI Appendix: Computing mutual information). The mere fact that τ is a function of ε c and ε r (in Eq. 2) means that I(τ; μ) ≤ I(ε c,ε r; μ), i.e., the predictive information of τ is bounded above by the predictive information of the pair of energies ε c and ε r. This inequality is a direct consequence of the Data Processing Inequality, a basic result in information theory (22). In our case, equality between I(τ; μ) and I(ε c,ε r; μ) can be achieved only if τ preserves all of the transcriptionally relevant information encoded in the predicted values for ε c and ε r. We emphasize that there is no a priori guarantee that any quantity τ can do this, let alone a quantity derived from a simple biophysical model.
Remarkably we find (on full-wt data) that I(τ; μ) = 0.732 ± 0.007 bits, which is identical within error bars to I(ε c,ε r; μ) = 0.732 ± 0.006 bits. We believe this equality is an important validation of the specific thermodynamic formula used to represent τ (Eq. 2). This agreement also argues that our energy matrix models for ε c and ε r provide a valid representation of physical binding energy; if they did not, their use in the Boltzmann exponents in Eq. 2 would be unlikely to yield sensible results. We note that a simpler model in which transcription depends only linearly on ε c and ε _r_—which would be appropriate if CRP and RNAP bound DNA only as a complex—achieves only I(ε c + ε r; μ) = 0.647 ± 0.005 bits when all parameters are fit ab initio to full-wt data. This value is significantly less than I(ε c,ε r; μ). Our specific thermodynamic model for τ, with its physically motivated functional form, therefore provides a marked improvement over the more naive linear model.
Discussion
The approach we present here can be applied to a wide variety of TRSs in a number of different organisms. No prior knowledge of a TRS’s sequence architecture is needed. All that is required is that (i) the TRS of interest function on a reporter construct and (ii) a large library of reporter constructs be introduced into cells so that each cell receives a single mutant TRS. After the activity-based partitioning and sequencing of mutant TRSs, information footprints can be used to identify all functionally relevant positions within the probed sequence. Information footprints from experiments performed in growth conditions or genetic backgrounds that are known to affect expression can further help one identify which “clumps” of informative positions correspond to discrete binding sites, as well as which of these sites are involved in transducing specific intracellular signals. Eq. 1 then allows one to infer mathematical models describing the sequence-dependent binding energy of each site’s cognate protein. The same fitting procedure can also be used to build biophysical models of the in vivo interactions between multiple DNA-bound proteins. Such inference requires no quantitative model of experimental noise, thus allowing experiments performed in very different ways to produce nearly identical results.
GFP reporter plasmids have been constructed for almost all E. coli promoters (21). Starting from these plasmids and using our protocols, it should be possible to biophysically characterize the vast majority of promoters in E. coli. Similar experiments can likely be performed for most TRSs in yeast. While we demonstrated our technique on a TRS containing only two protein binding sites, the great sensitivity of this approach should allow the simultaneous effects of many DNA-binding proteins (including nucleosomal proteins) to be discerned from a single experiment. Ultimately, our method should be useful for characterizing the detailed functional architecture of TRSs active in a wide variety of culturable cells, including stem cells and cancer cell lines. The biophysical characterization of TRSs in living animals, however, will likely require significant changes to the experimental approach described here.
The underlying principles of our approach should also be useful for studying many different systems in which sequence-dependent interactions (e.g. protein-DNA, protein-RNA, protein-protein or protein-ligand interactions) play a central role in establishing some activity of interest. Experiments like ours can be performed both in vivo and in vitro; one simply needs to partition a large number of mutant sequences according to each one’s activity. Our analysis method should then allow quantitative models of sequence-dependent function to be rigorously inferred from the resulting sequence data, regardless of how the activity-dependent partitioning of sequences is accomplished.
Experimental Procedures
See SI Appendix: Supporting experimental procedures for an expanded explanation of our experimental procedures.
Strains.
E. coli strains MG1655 (wild type) and TK310 (Δ_cyaA_ Δ_cpdA_ Δ_lacY_) were kindly provided by Thomas Kuhlman. Except where noted, TK310 cells were maintained in media supplemented with 500 μM cAMP in order to prevent crp_-mediated suppression of Δ_cyaA (32).
Library Construction.
Mutant lac promoter libraries were synthesized using defined mixtures of nucleoside phoshporamidites. Plasmid libraries consisted of ∼2 × 106 independently cloned plasmids in which region [-75∶-1] was exactly replaced without the introduction of artificial restriction sites (SI Appendix: Plasmid library construction)
Sorting.
Cells were grown in exponential phase for ≥10 generations, diluted into buffer, and stored on ice for 0–24 h prior to sorting. A BD Biosciences FACSVantage SE with DiVa was then used to sort 100,000 cells into each batch based solely on GFP fluorescence. Plating revealed ∼70,000 viable cells per batch.
Amplicon Generation and Sequencing.
Miniprepped plasmid from each FACS batch was used as template for amplicon-generating PCR. Two control sets of amplicons were also generated from pUA66-lacZ plasmid. The 47 resulting amplicon libraries (45 FACS batches + 2 wild-type controls) were collated and sequenced by Roche using the Genome Sequencer FLX platform. This yielded 448,416 sequences, 308,309 of which passed our quality filters. Unfortunately, an analysis of these sequences indicated a large postsort reduction in sequence diversity (SI Appendix: Post-sort loss of library diversity). To guarantee that each sequence was independently sorted, we discarded all but one copy of each sequence in each batch, leaving a total of 220,591 sequences across our six experiments.
Sequence Data and Analysis Results.
Our 454 sequence data is available on the NCBI website under accession number SRA012345. Additional information, including processed sequence reads and inferred model parameters, is available at http://www.princeton.edu/~ccallan/sortseq09/.
Supplementary Material
Supporting Information
Acknowledgments.
We thank Christina DeCoste, who assisted with all flow cytometry instrumentation. Amy Caudy, Thomas Kuhlman, and Paul Wiggins provided critical advice on various experimental issues. Sean Eddy and Rob Phillips provided valuable feedback on the manuscript. We further benefited from discussions with William Bialek, Thomas Gregor, Stanislav Shvartsman, Antoinette Sutto, Gašper Tkačik, and Michael Zhang. The work of C.G.C., J.B.K., and A.M. was supported in part by National Science Foundation Grant PHY-0650617. The work of J.B.K. and E.C.C. was supported in part by National Institutes of Health Grants GM078591 and GM071508. The work of J.B.K. was supported in part by the Simons Foundation. The work of C.G.C. was supported in part by Department of Energy Grant DE-FG02-91ER40671.
Footnotes
The authors declare no conflict of interest.
Data deposition: The sequence reported in this article has been deposited in the NCBI database (accession number SRA01234).
References
- 1.Ren B, et al. Genome-wide location and function of DNA binding proteins. Science. 2000;290:2306–2309. doi: 10.1126/science.290.5500.2306. [DOI] [PubMed] [Google Scholar]
- 2.Johnson D, Mortazavi A, Myers R, Wold B. Genome-wide mapping of in vivo protein-DNA interactions. Science. 2007;316:1497–1502. doi: 10.1126/science.1141319. [DOI] [PubMed] [Google Scholar]
- 3.Berg O, von Hippel P. Selection of DNA binding sites by regulatory proteins. II. The binding specificity of cyclic AMP receptor protein to recognition sites. J Mol Biol. 1988;200:709–723. doi: 10.1016/0022-2836(88)90482-2. [DOI] [PubMed] [Google Scholar]
- 4.Tuerk C, Gold L. Systematic evolution of ligands by exponential enrichment: RNA ligands to bacteriophage T4 DNA polymerase. Science. 1990;249:505–510. doi: 10.1126/science.2200121. [DOI] [PubMed] [Google Scholar]
- 5.Meng X, Brodsky MH, Wolfe SA. A bacterial one-hybrid system for determining the DNA-binding specificity of transcription factors. Nat Biotechnol. 2005;23:988–994. doi: 10.1038/nbt1120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Berger M, et al. Compact, universal DNA microarrays to comprehensively determine transcription-factor binding site specificities. Nat Biotechnol. 2006;24:1429–1435. doi: 10.1038/nbt1246. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Carey MF, Peterson CL, Smale ST. Transcriptional regulation in eukaryotes: concepts, strategies, and techniques. Cold Spring Harbor: Cold Spring Harbor Laboratory Press; 2009. [Google Scholar]
- 8.Ptashne M, Gann A. Genes and signals. Cold Spring Harbor: Cold Spring Harbor Laboratory Press; 2002. [Google Scholar]
- 9.Müller-Hill B. The lac operon: a short history of a genetic paradigm. Berlin: Walter de Gruyter; 1996. [Google Scholar]
- 10.Vilar JMG, Leibler S. DNA looping and physical constraints on transcription regulation. J Mol Biol. 2003;331:981–989. doi: 10.1016/s0022-2836(03)00764-2. [DOI] [PubMed] [Google Scholar]
- 11.Kuhlman T, Zhang Z, Saier MH, Hwa T. Combinatorial transcriptional control of the lactose operon of Escherichia coli. Proc Natl Acad Sci USA. 2007;104:6043–6048. doi: 10.1073/pnas.0606717104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Busby S, Ebright RH. Transcription activation by catabolite activator protein (CAP) J Mol Biol. 1999;293:199–213. doi: 10.1006/jmbi.1999.3161. [DOI] [PubMed] [Google Scholar]
- 13.Bintu L, et al. Transcriptional regulation by the numbers: models. Curr Opin Genet Dev. 2005;15:116–124. doi: 10.1016/j.gde.2005.02.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Fakhouri WD, et al. Deciphering a transcriptional regulatory code: modeling short-range repression in the Drosophila embryo. Mol Syst Biol. 2010;6:341. doi: 10.1038/msb.2009.97. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Schneider T, Stormo G. Excess information at bacteriophage T7 genomic promoters detected by a random cloning technique. Nucleic Acids Res. 1989;17:659–674. doi: 10.1093/nar/17.2.659. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Kinney JB, Tkačik G, Callan CG., Jr. Precise physical models of protein-DNA interaction from high-throughput data. Proc Natl Acad Sci USA. 2007;104:501–506. doi: 10.1073/pnas.0609908104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Herzenberg L, Sweet R, Herzenberg L. Fluorescence-activated cell sorting. Sci Am. 1976;234:108–117. doi: 10.1038/scientificamerican0376-108. [DOI] [PubMed] [Google Scholar]
- 18.Margulies M, et al. Genome sequencing in microfabricated high-density picolitre reactors. Nature. 2005;437:376–380. doi: 10.1038/nature03959. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Segal E, Raveh-Sadka T, Schroeder M, Unnerstall U, Gaul U. Predicting expression patterns from regulatory sequence in Drosophila segmentation. Nature. 2008;451:535–540. doi: 10.1038/nature06496. [DOI] [PubMed] [Google Scholar]
- 20.Gertz J, Siggia ED, Cohen BA. Analysis of combinatorial cis-regulation in synthetic and genomic promoters. Nature. 2009;457:215–218. doi: 10.1038/nature07521. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Zaslaver A, et al. A comprehensive library of fluorescent transcriptional reporters for Escherichia coli. Nat Methods. 2006;3:623–628. doi: 10.1038/nmeth895. [DOI] [PubMed] [Google Scholar]
- 22.Cover TM, Thomas JA. Elements of information theory. New York, NY: Wiley; 1991. [Google Scholar]
- 23.Patwardhan RP, et al. High-resolution analysis of DNA regulatory elements by synthetic saturation mutagenesis. Nat Biotechnol. 2009;27:1173–1175. doi: 10.1038/nbt.1589. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Ross W, et al. A third recognition element in bacterial promoters: DNA binding by the alpha subunit of RNA polymerase. Science. 1993;262:1407–1413. doi: 10.1126/science.8248780. [DOI] [PubMed] [Google Scholar]
- 25.Reznikoff WS. The lactose operon-controlling elements: a complex paradigm. Mol Microbiol. 1992;6:2419–2422. doi: 10.1111/j.1365-2958.1992.tb01416.x. [DOI] [PubMed] [Google Scholar]
- 26.Takeda Y, Sarai A, Rivera VM. Analysis of the sequence-specific interactions between Cro repressor and operator DNA by systematic base substitution experiments. Proc Natl Acad Sci USA. 1989;86:439–443. doi: 10.1073/pnas.86.2.439. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Sarai A, Takeda Y. Lambda repressor recognizes the approximately 2-fold symmetric half-operator sequences asymmetrically. Proc Natl Acad Sci USA. 1989;86:6513–6517. doi: 10.1073/pnas.86.17.6513. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Man TK, Stormo GD. Non-independence of Mnt repressor-operator interaction determined by a new quantitative multiple fluorescence relative affinity (QuMFRA) assay. Nucleic Acids Res. 2001;29:2471–2478. doi: 10.1093/nar/29.12.2471. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Maerkl SJ, Quake SR. A systems approach to measuring the binding energy landscapes of transcription factors. Science. 2007;315:233–237. doi: 10.1126/science.1131007. [DOI] [PubMed] [Google Scholar]
- 30.Harley CB, Reynolds RP. Analysis of E. coli promoter sequences. Nucleic Acids Res. 1987;15:2343–2361. doi: 10.1093/nar/15.5.2343. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Gunasekera A, Ebright YW, Ebright RH. DNA sequence determinants for binding of the Escherichia coli catabolite gene activator protein. J Biol Chem. 1992;267:14713–14720. [PubMed] [Google Scholar]
- 32.Harman JG, Dobrogosz WJ. Mechanism of CRP-mediated cya suppression in Escherichia coli. J Bacteriol. 1983;153:191–199. doi: 10.1128/jb.153.1.191-199.1983. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supporting Information