Probing the Disordered Domain of the Nuclear Pore Complex through Coarse-Grained Molecular Dynamics Simulations (original) (raw)

Abstract

The distribution of disordered proteins (FG-nups) that line the transport channel of the nuclear pore complex (NPC) is investigated by means of coarse-grained molecular dynamics simulations. A one-bead-per-amino-acid model is presented that accounts for the hydrophobic/hydrophilic and electrostatic interactions between different amino acids, polarity of the solvent, and screening of free ions. The results indicate that the interaction of the FG-nups forms a high-density, doughnut-like distribution inside the NPC, which is rich in FG-repeats. We show that the obtained distribution is encoded in the amino-acid sequence of the FG-nups and is driven by both electrostatic and hydrophobic interactions. To explore the relation between structure and function, we have systematically removed different combinations of FG-nups from the pore to simulate inviable and viable NPCs that were previously studied experimentally. The obtained density distributions show that the maximum density of the FG-nups inside the pore does not exceed 185 mg/mL in the inviable NPCs, whereas for the wild-type and viable NPCs, this value increases to 300 mg/mL. Interestingly, this maximum density is not correlated to the total mass of the FG-nups, but depends sensitively on the specific combination of essential Nups located in the central plane of the NPC.

Introduction

Fast and selective transportation of macromolecules between the cytoplasm and the nucleoplasm is essential for the proper functioning of eukaryotic cells. This is accomplished by the nuclear pore complex (NPC), which is embodied in the nuclear envelope membranes and moderates the transport of molecules in a size-selective manner. The NPC is a large molecular assembly with an estimated mass of 44–70 MDa for yeast (1,2) that provides bidirectional pathways for passive transport of small molecules and facilitated transport of larger proteins (3–8). The active transport mechanism of large macromolecules is directional and is driven by soluble nuclear transport factors (NTF), which mostly belong to the Karyopherin family (Kap). During import or export, the appropriate NTF binds to cargo with nuclear import or export signals, upon which the NTF-cargo complex is translocated through the NPC.

The NPC has an eightfold symmetrical structure and is composed of ∼30 different proteins called nucleoporins (Nups) (2,9). The Nups fall into different subgroups based on their function: transmembrane Nups that attach the NPC to the membrane, structured Nups that form the core scaffold of the NPC and maintain its shape, and, finally, FG-nups. The FG-nups comprise ∼30% of all Nups and are found to be intrinsically disordered and have many phenylalanine-glycine (FG) repeats in their amino-acid sequence (10). They line the central channel of the NPC and are anchored to the scaffold through their structural domain. These FG-nups have been shown to be essential for the viability of yeast and presumably all eukaryotes (11). However, how the biophysical properties of the FG-nups determine their function in passive and active transport is subject to intense debate.

Different models have been proposed to explain the role of the FG-nups during nuclear transport.

The selective phase model, for instance, presumes that the weak FG-FG interactions form a homogeneous cross-linked network (a hydrogel) inside the NPC. The Kaps can locally break the cross-links in the network and melt through the gel due to their higher affinity to the FG-repeats (compared to FG-FG affinities); the space between the cross-links serve as a sieve and allows for free diffusion of smaller molecules (12).

The virtual gate model suggests that the brush-like structure formed by the disordered FG-nups repels nonspecific cargoes, but allows Kap-associated cargoes to overcome this entropic barrier because of the low-affinity interactions between the Kaps and the FG-repeats (13).

The reversible collapse model can be considered as an extension of the virtual gate model in which the active transport is facilitated by a conformational change of the FG-nups due to the presence of the Kaps (14). The interaction between Kaps and FG-nups results in a local collapse of the Nups toward their anchor point, providing enough space for translocation of the Kap-cargo complex.

The reduction-of-dimensionality model suggests that the wall of the transport channel is covered with an FG-NTF bilayer, leaving a 5–10 nm tube for passive diffusion of small molecules at the center of the pore. The active transport is then facilitated by a two-dimensional random walk of the Kaps over the NTF surface (5,15).

The forest model is based on the Stokes radius and dimension of the individual FG-nup domains. Those FG-nups that have a fully collapsed conformation form shrub-like structures near the scaffold, and those that consist of an extended domain next to a collapsed domain form tree-like structures, resembling an FG-nup forest landscape. It has been proposed that this configuration forms two distinct transport pathways, one at the center and the other near the scaffold, which are used for active and passive transport, respectively (16). However, no consensus has been reached so far on a prevailing model.

One reason hampering the understanding of nuclear transport is the absence of experimental techniques that can probe the structure and dynamics of the disordered proteins inside the transport channel and during transport. This has led to the development of computational approaches to gain insight on the conformation of the FG-nups inside the NPC. Due to the large size of the system, high-resolution (all-atom) molecular-dynamics simulations are restricted to study only single FG-nups (16,17) or a periodic array of short FG-nup segments, end-grafted on a flat surface (18,19). On the other hand, several low-resolution approaches have been used to study the transport rate and accumulation of cargo molecules inside the NPC without considering the detailed interactions between the FG-nups (20–23). Due to the high level of coarse-graining, the full geometry of the NPC can be accounted for in these approaches, but at the expense of losing detail at the scale of individual amino acids (24). Recently, Tagliazucchi et al. (25) developed a computational model that accounts for the amino-acid sequence of the FG-nups by distinguishing six different families of amino acids. Then, FG-nups are distributed along the channel tethered to the surface of the NPC-scaffold and minimization of free energy is applied subject to axisymmetric boundary conditions. Using this model, they studied the translocation of model particles through the NPC.

The goal of this article is to probe the full three-dimensional disordered domain of the yeast nuclear pore complex by accounting for all FG-nups, each having a complete 20 amino-acid resolution. Our one-bead-per-amino-acid molecular dynamics approach is based on experimentally obtained hydrophobicity scales and calibrated against experimental Stokes radii of a wide range of FG-nup segments (16). Using the model, we will study the effect of electrostatic and hydrophobic interactions on the FG-nup conformation and explore the relation between FG-nup distribution and cell viability, as studied using genetically modified yeast strains (11).

Methods

A coarse-grained molecular-dynamics model is developed in which each amino acid is represented by one bead. An average mass of 120 Da is assigned to each bead and the distance between neighboring beads is fixed at b = 0.38 nm using a stiff harmonic potential,

ϕbond=Kb(r−b)2withKb=8038kJ⋅nm−2⋅mol−1.

The bending and torsion potentials for the coarse-grained model are extracted from the Ramachandran data of the coiled regions of protein structures as discussed earlier (26). It is widely accepted that FG-nups are intrinsically disordered and highly flexible, without evidence of secondary structure formation (10,16,27,28). This indicates that no stable, long-lasting hydrogen bonds are formed. In line with this, hydrogen bonding is not incorporated in our model. Because solvent molecules are not modeled explicitly, the solvent-residue interactions are accounted for through hydrophobic and hydrophilic interactions between the amino-acid residues. In addition, the screening effect of polar water molecules and free ions and the electrostatic interactions among charged amino acids are accounted for through a modified Coulomb law. To take into account both attractive hydrophobic and repulsive hydrophilic interactions with one function, the following potential is proposed as

ϕhp(r)={εrep(σr)8−εij[43(σr)6−13]r≤σ(εrep−εij)(σr)8σ≤r, (1)

where

is the strength of the interaction for each pair of amino acids (i, j), and σ = 0.60 nm is the average residue diameter (29). The choice for the exponent 8 for the repulsive interactions has been made to have a softer repulsive potential (29) and thus a smoother energy landscape. The prefactors are chosen such that the potential and its derivative are continuous at r = σ. The hydrophobicity scales obtained from partition energy measurements (30–32) are normalized between 0 and 1, and the average value of the experimental data is used to define the relative hydrophobic strength for each amino acid ε i ∈[0,1] (see Table S1 and Table S2 in the Supporting Material). The _ε_hp can be interpreted as the absolute hydrophobic strength between the most hydrophobic amino acids, whereas _ε_rep defines the intensity of the repulsive hydrophilic interactions. When ε ij > _ε_rep, the potential is attractive (hydrophobic interactions); when ε ij = _ε_rep, the potential is neutral, only accounting for excluded volume effects until r = σ; and when ε ij < _ε_rep, the potential is purely repulsive (hydrophilic interactions). The electrostatic interactions between charged amino acids are described by the modified Coulomb law as

ϕel=qiqj4πε0εr(r)rexp(−κr). (2)

Because experiments suggest that the nuclear envelope is not a selective ion barrier (33), a Debye screening coefficient similar to that of the cytoplasm, κ = 1.0 nm−1, is chosen (34). The distance-dependent dielectric constant of the solvent ε r(r) is included through the sigmoidal function

εr(r)=Ss[1−r2z2er/z(er/z−1)2],

where _S_s = 80, and z = 0.25 nm (35,36).

The parameterization procedure starts by choosing the values of _ε_rep and _ε_hp to be 10.0 and 13.0 kJ.mol−1, respectively, to set the minimum energy for the interaction of the most hydrophobic amino acids to −5.2 kJ.mol−1, as suggested in Zhang and Kim (37). Then, by using the experimental hydrophobicity scales of Table S1, the exponent α is chosen such that the model can reproduce the experimental Stokes radius of one of the low-charge FG-Nup segments (i.e., Nup42 (AA 1–212) (16)). With α = 0.27, the strength (hydrophilicity) of the three charged amino acids D, E, and K (assumed to be equal) is determined to capture the Stokes radius of a highly charged FG-nup segment (i.e., Nup116s (AA 765–960) (16)) within 5% error. By doing so, the interaction strength between polar amino acids is smaller than k_B_T, which is in accordance with the polar nature of these residues. Furthermore, the hydrophobicity scales of Proline, Glutamine, and Glycine are fine-tuned to reproduce the experimental end-to-end distances of poly-Proline segments (38), the dimension of poly-Glutamine segments with different lengths (39), and the experimental gyration radius of poly-Glycine chains (40), respectively. The final hydrophobicity scales ε i are presented in Table S2.

Although the Stokes radii of only two FG-nup segments are used to obtain α and ε i, the Stokes radii of the rest of the 16 FG-nup segments are predicted within 20% error with respect to the experimental values (see Fig. 1 and see Table S3). It should be noted that this accuracy cannot be achieved without considering repulsive interactions between hydrophilic amino acids. The performance of the force field for the collective interaction of FG-nups is verified by simulating an array of Nup62, end-grafted on a flat surface (see Fig. S1 in the Supporting Material). The computed brush height of h = 13 nm compares well with the experimental value, h = 14.1 nm (41).

Figure 1.

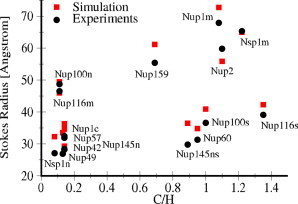
Figure 1

The predicted and experimental R s values for FG-nup segments plotted against the charge to hydrophobicity ratio (C/H). To see this figure in color, go online.

A simplified geometrical model of the NPC is built based on the geometry of the core scaffold of the yeast NPC, and the FG-nups are anchored at the predicted positions inside the pore (42,43), as shown in Fig. 2. Table S4 lists the FG-nups with the coordinates of the anchor points specified in Table S5. Locations of the FG-repeats and charged amino acids in the sequence of the FG-nups are depicted in Fig. 2 B. Because the spatial organization and surface properties of the structural Nups of the scaffold are not yet fully determined, the scaffold is modeled using hard-sphere beads with a radius of 2.5 nm, which are assumed to have no specific interaction with the FG-nups. The initialization procedure and the details regarding the molecular-dynamics simulations are given in the Supporting Material.

Figure 2.

Figure 2

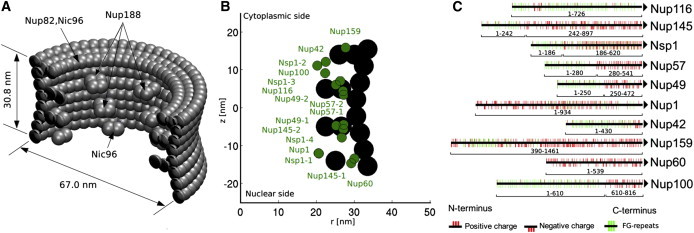
(A) Simplified geometry of the core scaffold of the yeast nuclear pore complex reconstructed based on the model of Alber et al. (42,43). The outer radius of the scaffold changes from 30 nm at the center to 33.5 nm at the peripheries. The inner blobs, which are decorated in eightfold rotational symmetry, represent Nup188 of the inner rings. The blobs at the cytoplasmic ring represent Nup82 and Nic96, whereas the ones at the nuclear ring represent Nic96. (B) The circumferential projection of radial and axial positions of the anchor points of the FG-nups. (C) The distribution of charged amino acids (red sticks) and FG-repeats (green sticks) in the sequence of the FG-regions of the FG-nups as used in the model. All Nups are anchored to the scaffold at their C-terminus. To see this figure in color, go online.

Results

Distribution of the FG-nups inside the NPC

To begin, the distribution of the FG-nups inside the NPC is investigated. The three-dimensional density distribution of the FG-nups is obtained by calculating the average number density of the amino acids over the simulation time. An iso-surface plot corresponding to 140 mg/mL mass density (0.7 nm−3 number density) is shown in Fig. 3 A. The results show a low-density region up to r ∼ 5 nm from the central axis of the NPC surrounded by a high-density region. The distribution is further analyzed by studying the distribution of the charged residues and FG-repeats inside the NPC. The charged amino acids (i.e., D, E, K, and R; see Table S2) are accumulated near the scaffold in between the inner ring blobs (Nup188 (42)) (see Fig. 3 B). The FG-repeats are distributed in the form of a doughnut between the central low-density region and the highly-charged layer near the scaffold (see Fig. 3 C). Because the distribution of the FG-nups is relatively homogeneous in the circumferential direction, it can be averaged to generate a two-dimensional, _r_-z density map (see Fig. 4 A). It shows that the FG-doughnut is located slightly above the central plane of the NPC (z ∼ 4.5 nm) toward the cytoplasmic side. Furthermore, the two-dimensional density maps of different residues can be averaged in the vertical direction to obtain the radial density profiles. The radial-density distribution of the FG-repeats and negatively and positively charged amino acids are plotted in Fig. S2. The FG-repeat distribution shows a peak value at r = 13 nm from the central axis of the NPC whereas the peak values for the negative and positive amino acids are at r = 20 nm and r = 21 nm, respectively. Moreover, the charge distribution shows that the central region of the pore has a net positive charge, which is consistent with the simulation results of Tagliazucchi et al. (25).

Figure 3.

Figure 3

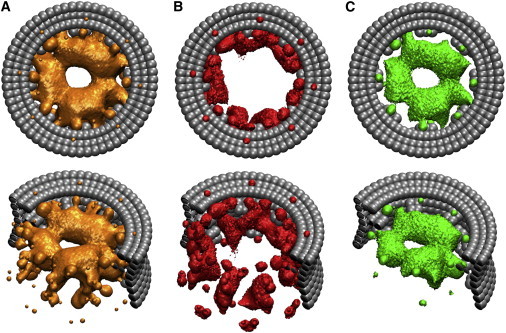
The three-dimensional density distribution of different amino acids inside the NPC obtained from the wild-type-1 simulation. (A) The distribution of all amino acids. The iso-surface plot corresponds to a mass density of 140 mg/mL. (B) The density distribution of charged amino acids. The iso-surface plot corresponds to a mass density of 22 mg/mL. (C) The density distribution of FG-repeats inside the transport channel of the NPC. The iso-surface plot corresponds to an average distance of 2.7 nm between the FG-repeats. To see this figure in color, go online.

Figure 4.

Figure 4

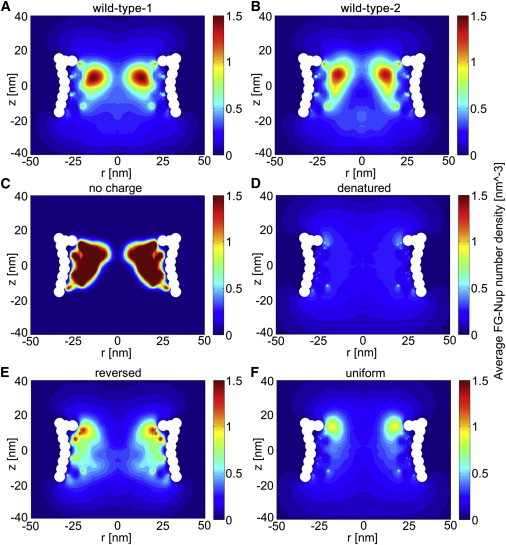
Two-dimensional density plots of the FG-nups in the simulated NPCs. (A) Wild-type-1 NPC. (B) Wild-type-2 NPC, simulated with a different starting configuration and initial velocity distribution compared to wild-type-1. (C) No-charge NPC, in which all charged residues are replaced by neutral beads in the sequence of the FG-nups. (D) Denatured NPC, where all residues are replaced by neutral beads. (E) Reversed NPC, where the FG-nups are anchored from their N-terminus. (F) Uniform NPC, in which the sequence of the FG-nups is modified such that they have a uniform distribution of charged and hydrophobic amino acids along their length. To see this figure in color, go online.

The conformation of the FG-nups inside the pore is found to be notably different from that of the isolated FG-nups: the ratio of the R g values for the FG-nups inside the NPC to the gyration radius of the isolated FG-nups ranges from 3.9 to 6.5 (see Table S4). A second simulation (wild-type-2) with the same FG-nups but different starting configuration and initial velocity distribution is performed to study the sensitivity to the initial conditions (the method to generate starting configurations is discussed in the Supporting Material). The two-dimensional density distribution (Fig. 4 B) shows the same characteristics as that of the first simulation (wild-type-1, Fig. 4 A). In addition, the localization of the individual FG-nups is similar in both simulations, which confirms that the obtained results are not biased by the simulation setup (see Fig. S5 and Fig. S6). Furthermore, there are uncertainties regarding the exact position of the anchor points of the FG-nups according to the experimental data (43). To investigate the sensitivity to the anchor-point locations, we performed a new simulation (wild-type-3) in which the anchor points are displaced in a random direction. The coordinates of the anchor points for wild-type-3 are displaced by randomly picking a new position inside a sphere of radius 4 nm around the old position (see Table S5). The obtained density distribution has the same pattern as that of the first and second simulations, as shown in Fig. S3 A. We conclude that small deviations in the anchor-point locations of the FG-nups do not affect the overall distribution of the FG-nups.

To study the sensitivity of the results to the geometry of the scaffold, an additional simulation has been performed using a symmetric geometry without inner blobs and peripheral rings (i.e., without Nup82, Nup188, and Nic96). The results show that the overall distribution of the FG-nups does not considerably change except for a slight shift of the _r_-position of the high-density region toward the scaffold (see Fig. S3 B). From this, we conclude that the asymmetric distribution of the FG-nups is due to the presence of different FG-nups on the nucleoplasmic and cytoplasmic sides of the NPC (Nup116, Nup100, Nup42, and Nup159 on the cytoplasmic side and Nup1, Nup145, and Nup60 on the nucleoplasmic side).

To study the localization of the individual FG-nups inside the pore, the two-dimensional (_r_-z) density distribution is calculated for all FG-nups that are anchored at the same (r,z) coordinates (see Fig. S5 and Fig. S6). The results reveal that some of the FG-nups (i.e., Nup49, Nup57, Nup116, Nup100, Nup42, and Nup145-2) are confined inside the pore and contribute in forming the central high-density region. The rest of the FG-nups (i.e., Nsp1, Nup159, Nup145-1, Nup60, and Nup1) have more conformational freedom and are spread out over a larger volume at both sides of the NPC.

Effect of hydrophobic and electrostatic interactions on the distribution of the FG-nups

The contribution of the hydrophobic and electrostatic interactions in shaping the distribution of the FG-nups inside the wild-type NPC is systematically studied. To begin, the wild-type NPC is modified by removing the charged residues, D, E, K, and R, and replacing them with neutral beads (i.e., residues of radius 0.6 nm with no specific attraction, repulsion, or charge interaction). The resulting density plot in this no-charge NPC shows that by removing charged amino acids, all FG-nups aggregate in a wide, high-density region, leaving an empty region at the center of the NPC (Fig. 4 C). In a next step, the rest of the amino acids are also replaced with neutral beads, resulting in a denatured NPC. The obtained distribution for the denatured NPC shows a uniform distribution of low density throughout the pore (Fig. 4 D). The results indicate that repulsive interactions between the charged amino acids in the wild-type NPC serve as a bumper to push the dense FG-nup clusters, formed through hydrophobic interactions, toward the center of the pore. Therefore, the doughnut-like structure in Fig. 3 is a direct result of the balance between the electrostatic and hydrophobic interactions. This balance is strongly related to the amino-acid sequence of the FG-nups, showing a high number of charged residues near the C-terminal domain (Fig. 2 B).

Effect of amino-acid sequence

Next, we explore the effect of the FG-nup amino acid sequence on the density distribution in the wild-type NPC. To do so, we anchored the FG-nups from their N-terminus to the same anchoring points. The distribution for this reversed NPC is shown in Fig. 4 E. Finally, a uniform NPC is simulated where the residues in the sequence of the FG-nups are reshuffled such that the charged and hydrophobic amino acids become uniformly distributed along their length (Fig. 4 F). To do so, the hydrophobic and charged amino acids are first evenly distributed in the sequence of the FG-nups and then the rest of the amino acids are randomly placed in between them. The density distributions for both the reversed and uniform NPC are different from the wild-type NPC. In the reversed case, the high-density region has shifted toward the scaffold on the cytoplasmic side. For the reversed and the uniform NPC, a wide, low-density region is detected at the center of the pore. A density concentration can be observed near the cytoplasmic entrance of the pore, but with a lower peak density compared to the wild-type NPC. In these two cases, the amino-acid composition of the FG-nups (percentage of charged and hydrophobic amino acids) has not changed compared to the wild-type NPC, suggesting that the amino-acid sequence of the FG-nups plays a key role in the density distribution of the FG-nups in the wild-type NPC. It should be noted that all simulations in Fig. 4 are performed for the same number of beads. The large difference in intensity between, e.g., Fig. 4, C and D, is due to the much larger region over which the residues are spread for the case of denatured proteins (Fig. 4 D).

Viable versus inviable NPCs

Experiments have shown that cells can survive despite deletion of more than half of the mass of the FG-repeats of the FG-nups (11). More specifically, Strawn et al. (11) showed that the presence of Nup100 or Nup116 is necessary but not sufficient. They proposed that if Nup116 is present and Nup100 is not, any combination of two of the four nups, Nsp1, Nup49, Nup57, or Nup145, are required, and conversely, if Nup100 is present and Nup116 is not, three of the mentioned four FG-nups must be present. We now explore a possible relation between cell viability and FG-nup density distribution by studying two extremes: a viable NPC with the least amount of essential FG-nups (minimal mass), and inviable NPCs with maximal mass of the FG-nups (see Table 1). The viable NPC includes all the FG-nups anchored near the central plane of the NPC (see also Fig. 2 B). The importance of Nup116 and Nup100 is investigated by removing only those two Nups (inviable-2). For the other four simulated inviable cases, Nup116 and two of the four Nups, Nup49, Nup57, Nup145, or Nsp1 are removed from the pore.

Table 1.

The list of simulated viable and inviable NPCs and their composition

Simulation name Nups removed (11)
Viable Nup42, Nup159, Nup1, Nup60, Nup100, Nsp1, Nup145a
Inviable-1 Nup116, Nsp1, Nup49
Inviable-2 Nup116, Nup100
Inviable-3 Nup116, Nup145, Nup49
Inviable-4 Nup116, Nup57, Nup49
Inviable-5 Nup116, Nup145, Nsp1

The two-dimensional density distributions for all these cases are shown in Fig. 5. Although the viable NPC contains less mass than the inviable cases, it has formed a high-density ring region, similar to what was observed before in the wild-type NPCs (Fig. 4, A and B), whereas the inviable cases do not exhibit this. This difference is summarized in Fig. 6 in terms of the radial density distribution at the _z_-location of the maximum density (excluding the anchor points) for each simulated NPC. The maximum density for the inviable NPCs does not exceed 185 mg/mL, whereas, for the viable and wild-type NPCs, a maximum density of 300 mg/mL is reached.

Figure 5.

Figure 5

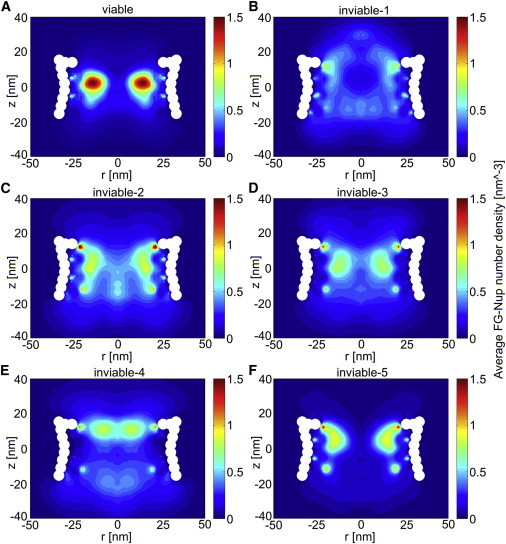
The two-dimensional density plots for viable (A) and inviable NPCs (B–F) corresponding to Table 1. To see this figure in color, go online.

Figure 6.

Figure 6

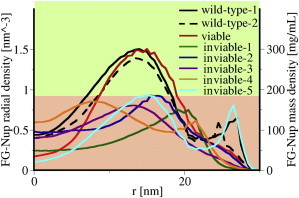
Comparison of the radial density distribution at the z location of maximal density in the two-dimensional density plots for the simulated NPCs. The mass density is calculated using an average mass of 120 Da per residue. To see this figure in color, go online.

Discussion and Conclusions

We have investigated the density distribution of the FG-nups inside the transfer conduit of the NPC. For this purpose, a one-bead-per-amino-acid coarse-grained model is developed that accounts for hydrophobic/hydrophilic and Coulombic interactions. The force field is parameterized and validated against experimental data of isolated FG-nup segments and FG-nup brushes. The model is fine enough to account for the sequence-dependent Stokes radius of individual FG-nups and coarse enough to study their collective behavior inside the three-dimensional geometry of the NPC. It should be noted, however, that all amino-acid beads are assumed to have the same size and mass and that no hydrogen bonding is accounted for. Solvent molecules are not included explicitly, but their polar nature and ionic screening are accounted for through the Coulombic and hydrophobic/hydrophilic interactions.

We show that the collective interaction of the FG-nups results in the formation of different zones inside the pore. A relatively low-density region is observed along the central axis of the NPC, which is surrounded by a coherent hydrophobic doughnut-like structure, rich in FG-repeats. It should be noted that earlier cryo-EM maps (9) have shown a high-density central-plug region at the center of the pore. However, it remains unclear whether this is due to cargo-molecules or FG-nups. The accumulation of charged residues is higher near the scaffold where the FG-nups are anchored, and the center of the NPC has a net positive charge in agreement with the simulation results of Tagliazucchi et al. (25). We show that the disruption of the FG-nup amino-acid sequence considerably changed the density distribution of the FG-nups (Fig. 4, E and F). This is in contrast to the results of Tagliazucchi et al. (25), and can be traced back to the different interaction energies used between hydrophilic amino acids. In Tagliazucchi et al. (25), an attractive interaction energy between hydrophilic amino acids of ∼1.0 k_B_T is used, whereas in our approach a repulsive interaction is defined between hydrophilic residues. The rationalization for the latter is that the favorable interaction between hydrophilic amino acids (including charged amino acids) and the solvent gives rise to a repulsive interaction between these amino acids. This is in accordance with the experimental observations of Yamada et al. (16), which show that the Stokes radius of short disordered segments of FG nups is correlated with the total number of charged amino acids and not with the net charge of these segments. As a result, it can be postulated that repulsive hydrophilic interactions are more important than Coulombic interactions in determining the dimensions of these proteins.

Comparison of the FG-nup distribution of viable and inviable NPCs suggests that the formation of a high-density hydrophobic structure, rich in FG-repeats, is a characteristic feature of viable NPCs. The contribution of the individual FG-nups to the total distribution is investigated through localization maps of all FG-nups inside the pore (see Fig. S5 and Fig. S6). The localization data suggest that FG-nups fall into two different categories: roughly half of the FG-nups contribute to the formation of the FG-repeat doughnut at the center of the NPC (i.e., Nup49, Nup57, Nup116, Nup100, Nup42, and Nup145-2), and the rest have more conformational freedom at the entrance and exit of the NPC (i.e., Nsp1, Nup159, Nup145-1, Nup60, and Nup1). The FG-repeats of the FG-nups in the latter category can facilitate the entrance of Kap/cargo complexes to the pore, whereas most of the FG-nups in the former category are marked as essential FG-nups, necessary for the viability of the cell (11).

Because it has been shown that the deletion of cohesive FG-nups or FG domains increases the permeability of the NPC (44,45), a possible reason for the inviability of the cells in the experiments of Strawn et al. (11) could be the disruption of the permeability barrier of the NPC. Our results show that even though the total mass of the FG-nups in the inviable mutant NPCs is larger than the viable mutant NPC, the density of the FG-nups does not exceed a certain value (i.e., 185 mg/mL). This indicates that the mutual interaction of an essential set of FG-nups is key in forming a doughnut-like hydrophobic cluster, rich in FG-repeats, which might control the NPC’s permeability barrier or, alternatively, its active transport mechanism. It must be noted that in the obtained results the possible effect of Kaps on the FG-nup density distribution is not taken into account.

It has been shown that Kaps simultaneously interact with up to four FG-repeats during transport (46). This suggests a correlation between the average distance of the FG-repeats inside the NPC and the distance between the binding sites on the surface of the Kaps. Experiments have revealed that the binding sites of NTF2 are separated by 3.5 nm (47) and simulation studies have shown that the distance between the binding spots of Kap _β_1 ranges from 2.5 to 4.0 nm (48). We have used the density distribution of the FG-nups to estimate the average distance between the FG-repeats inside the pore (see Fig. S4). The results show that inside the FG-doughnut the distance between the FG-repeats is lowest, reaching values as low as 2.7 nm. The same analysis for the uniform NPC (see Fig. 4 F) shows a minimum distance of 3.4 nm between the FG-repeats only in a small area near the cytoplasmic side of the NPC. This suggests that throughout the FG-doughnut, there is more than one FG-repeat available for each binding site so that the Kaps can easily find a nearby FG-repeat and translocate from one FG-repeat to the other (assuming that the presence of the Kaps does not considerably change the local conformation of the FG-nups). This is in accordance with the model of Bednenko et al. (49), which proposes that transport is accomplished through a series of binding and unbinding events between the FG-repeats and Kaps.

Single molecule tracking of small molecules, Imp-_β_1 and import complexes, has revealed two different but not completely separated pathways for active and passive transport (50). The spatial distribution of small molecules along the radius of the pore shows a peak value at the center of the NPC, whereas the distribution of Imp-_β_1 exhibits a peak closer to the scaffold. This is in agreement with the density distributions obtained from our simulations that show a low-density region of FG-nups at the center (which might allow passive diffusion of small molecules) and a peak density of FG-repeats at 13 nm along the radius of the NPC (which might mediate active transport).

Our model does not allow discriminating between the different transport models proposed in the literature. However, we do note that the shrubs and trees as described by the forest model (16) were not reflected in the obtained density distributions. A possible reason is that the forest model is based on the conformation of isolated FG-nups, which apparently is different from the conformation of the FG-nups inside the core of the NPC (see Table S4, last column). The density of the FG-nups inside the FG-doughnut is in correspondence to the densities (i.e., ≳ 200 mg/mL) at which a saturated hydrogel with selective barrier properties of the NPC can be formed (44,45,51), whereas, in the central region of the pore, the density of the FG-nups would be too low (i.e., ≤150 mg/mL) (51).

To conclude, we have studied the collective behavior of FG-nups inside the transport conduit of the nuclear pore complex through coarse-grained molecular dynamics simulations. The obtained density distribution of the FG-nups reveals the presence of a low-density region of diameter ≃10 nm at the center of the NPC, surrounded by a high-density, FG-repeat-rich region. We show that this unique doughnut-like distribution is encoded in the amino-acid sequence of the FG-nups and is driven by hydrophobic, hydrophilic, and electrostatic interactions. Our results indicate that the maximum FG-nup density correlates with the viability of the cells and is independent of the total mass of the FG-nups. Comparison of experimental observations with our results suggests that the low-density region at the center of the NPC provides a permeable medium through which ions and small proteins can freely diffuse, while the doughnut-like FG-repeat-rich region provides the required interaction sites for facilitated transport of Kap-cargo complexes. Further simulation studies are needed to confirm this.

Acknowledgments

The computations were carried out at the Centre for High Performance Computing and Visualization of the University of Groningen.

This work is supported by the Zernike Institute for Advanced Materials, University of Groningen.

Supporting Material

Document S1. Four equations, five tables, six figures, and supplemental information

Document S2. Article plus Supporting Material

Supporting Citations

References (52–63) appear in the Supporting Material.

References

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Document S1. Four equations, five tables, six figures, and supplemental information

Document S2. Article plus Supporting Material