Designing candidate gene and genome-wide case-control association studies (original) (raw)
. Author manuscript; available in PMC: 2014 Sep 30.
Published in final edited form as: Nat Protoc. 2007;2(10):2492–2501. doi: 10.1038/nprot.2007.366
Abstract
This protocol describes how to appropriately design a genetic association case-control study, either focussing on a candidate gene or region, or implementing a genome-wide approach. The steps described involve: 1) defining the case phenotype in adequate detail; 2) checking the heritability of the disease in question; 3) considering whether a population-based study is the appropriate design for the research question; 4) the appropriate selection of controls; 5) sample size calculations; and 6) giving due consideration to whether it is a de-novo or replication study. General guidelines are given, as well as specific examples of a candidate gene and a genome-wide association study into Type 2 Diabetes. Software and websites used in this protocol include the International HapMap Consortium website, Genetic Power Calculator, CaTS, and SNPSpD. Running each of the programmes only takes a few seconds; the rate-limiting steps involve thinking through the designs and parameters in the disease models.
Keywords: case-control, genetic, study design, candidate gene, genome-wide, power
INTRODUCTION
Genetic variation in DNA sequence influences risk of developing many diseases. Early studies investigated genetic variations underlying rare conditions that showed clear Mendelian segregation patterns through families (e.g. Huntington’s disease 1, cystic fibrosis 2); they were very successful in locating these genetic variations because they carried a 100% risk - and were the sole cause - of the disease. However, the search for genetic variants that underlie common ‘complex diseases’ (e.g. diabetes, cardiovascular disease, many cancers) has proven much more difficult. This is because each variant is only one of many genetic and environmental causal factors, each of which are neither necessary nor sufficient to individually cause the disease. Thus, they predispose to – rather than directly result in - its development. Finding those variants is important, because even a variant that results in a low increased RELATIVE RISK (see Glossary, Box 1) of a common condition may still have major public health importance in terms of the number of people affected because of it; moreover, such findings can uncover novel causal pathways worthy of further exploration.
BOX 1.
Glossary
RELATIVE RISK
A measure of increased/decreased risk comparing two groups; it is the ratio of disease risk in one group over another.
SINGLE NUCLEOTIDE POLYMORPHISM (SNP)
A genetic variant that consist of a single DNA basepair change, resulting in two possible allelic identities at that position.
LINKAGE DISEQUILIBRIUM (LD)
The population correlation between two (usually nearby) allelic variants on the same chromosome; they are in LD if they are inherited together more often than expected by chance.
POWER
The probability of a study to obtain a significant result if this result is true in the underlying population from which the study subjects were sampled.
POPULATION ALLELE FREQUENCY
The frequency of a particular allelic variant in a general population of specified origin.
CONFOUNDING
A type of bias in statistical analysis causing spurious or distorted findings, due to the existence of factors that are associated with disease risk as well as the exposure of interest
POPULATION STRATIFICATION
A situation of confounding in genetic studies, where cases and controls are not selected from the same population, and in which the subpopulations differ regarding the allele frequencies of the genetic variants under study and the prevalence of disease.
COVARIATE
Any variable other than the main exposure of interest that is possibly predictive of the outcome under study; covariates include confounding variables which, in addition, are associated with exposure.
ODDS RATIO
A measure of relative risk derived from case-control studies; it is the ratio of odds of disease in the exposed group over the non-exposed group.
HERITABILITY
The proportion of total variance of a continuous trait that is due to all underlying genetic factors; heritability of a binary condition, such as a disease, is calculated by considering disease development as a threshold that is reached on a scale of underlying continuous liability.
TYPE I ERROR
The probability of rejecting the null hypothesis of no effect of exposure on disease when in fact the null hypothesis is true. For genetic association studies, type I errors reflect false positive findings of associations between allele/genotype and disease.
With the unravelling of the Human Genome sequence and the identification of many DNA sites where individuals differ via the International HapMap 3 we now have the raw information required to find disease predisposing (or protective) genetic variants for complex traits 4. Phase II of HapMap provides information on the location of nearly four million common SINGLE NUCLEOTIDE POLYMORPHISMS (SNPs) across the genome in four populations of different ethnic origin (Caucasians of Northern & Western European origin; Japanese from Tokyo; Han Chinese from Beijing; and Yoruba from Nigeria). More importantly, within each population, HapMap provides information about the allelic association between SNPs located near each other, also termed ‘LINKAGE DISEQUILIBRIUM (LD)’. LD is the population-genomic feature used in genetic association studies to find the location of a disease-predisposing genetic variant. Knowing the LD structure, either in a candidate region or across the genome, helps the investigator to select a subset of SNPs that capture the majority of all common genetic variation because they predict the allelic status of other nearby SNPs (and thus also any common disease-predisposing variants) without having to genotype these variants themselves. How to select such ‘tagSNPs’ will be discussed in the next paper in this series.
There are two main types of genetic association studies: population-based case-control studies and family-based studies. Family-based association studies are often most efficiently aimed at finding rare variants underlying rare conditions or rare sub-phenotypes of a common condition. Their design is not the focus of this protocol. Population-based (defined here as non-family based) case-control studies have become the most popular design to find common polymorphisms thought to underlie complex traits (also termed ‘common disease common variant’ hypothesis’) 5. They can be hypothesis-driven candidate gene (CG) studies, focussing on a particular gene or area of the genome, or can involve genome-wide association (GWA) analyses conducted without prior hypotheses. Until recently, the success rate of candidate gene case-control studies was very poor. To illustrate, a review in 2002 of 603 published disease-genetic variant associations found that only 6 appeared to be independently replicated 6. Some investigators have interpreted this as evidence that most - if not all - complex traits are not caused by common genetic polymorphisms but by multiple rare ones 7, for which population-based case-control studies have little or no POWER of detection 5. However, most candidate gene studies carried out to date have been poorly designed in terms of case definition, control selection, genetic marker selection, and in particular sample size, and therefore cannot provide evidence for success or failure of their intended objectives either way. The potential for GWA studies has only recently materialised because of reductions in genotyping costs and more sophisticated specifications of the genotyping arrays in terms of SNP numbers and coverage (see next paper in this series). The latest products provide 300,000 – 1 million SNPs, supplemented by selected sets that are hypothesized to be of increased functional importance. Despite scepticism regarding their power to detect the modest effect sizes of common polymorphisms expected to underlie complex traits, examples of replicated findings have started to emerge 8-14.
The present protocol considers the appropriate design of both CG and GWA studies in terms of case and control definition, and determining minimum sample size to achieve adequate power. Marker selection strategies, quality control and basic data analysis will be discussed in separate protocols in this series.
Define the case/phenotype definition accurately
The first step in the design of a case-control study is to define the disease or phenotype of interest as accurately and specifically as possible. This is important because non-specific case definitions will increase both the genetic and environmental heterogeneity in underlying causal factors, and can therefore drastically decrease the power of detection of an effect. Secondly, replication of the study (a crucial part of the validation of the results found) will become impossible if the phenotype has not been adequately defined. Often a balance has to be achieved between phenotype definitions that are seen as clinically relevant (but which may not be highly specific) and those that are seen biologically relevant (which may be more specific but less clinically relevant). Such definitions are likely to change historically, as more clinical and biological information becomes available. For example, the diagnosis of the main subtypes of diabetes has grown more specific over the years, from ‘early-onset vs. adult-onset’ to ‘insulin-dependent vs non-insulin dependent’ to Type I/Type II, and most recently Type1/Type 2 15;16. Even the most recent definition of Type 2 is recognised as a heterogeneous condition with diverse molecular and environmental pathways 17. In addition, since recruitment of adequate numbers of cases within a highly specific disease definition is often difficult (i.e. requiring multi-centre studies), less specific definitions are frequently introduced to make up sufficient numbers in an attempt to attain a certain level of power. However, in reality a gain of power may not be achieved at all; a reduction in overall power may even be the result, because of increased causal heterogeneity. In practice, the best guideline is to define cases according to a definition that minimises the likely causal heterogeneity based on all existing clinical and biological evidence. For example, in a situation in which a clear, strong, environmental cause is already known for the condition in question, the investigator could limit case and control selection to those unexposed to this cause.
Is the disease heritable?
An obvious but sometimes overlooked element in deciding whether or not to pursue any genetic association study is to weigh up all evidence of familial aggregation studies that have investigated the HERITABILITY of the disease of interest. Heritability is assessed through studying disease patterns among family members, in particular comparing monozygotic (MZ) with dizygotic (DZ) twins. Increased concordance of disease status among MZ vs. DZ twins suggests a role for genetic factors, since DZ twins share, on average, half their genes whilst MZ twins are genetically identical. Diseases of low heritability (e.g. 10-20%) will likely need very large sample sizes to allow the finding of aetiological genetic variants, which will need to be considered. More importantly, if good evidence exists that the heritability of the phenotype in question is (close to) zero, little will be gained from conducting a genetic case-control study.
Is a population-based case-control study the right design for the research question?
There are several conditions that determine whether a population-based case-control study is suitable to answer specific research questions. First, such a study design is best suited to phenotypes for which several thousands of cases can be recruited to be able to detect the likely modest underlying genetic relative risks. The power of a case-control study can potentially be increased (and thus the number of cases required decreased) by recruiting cases with a family history of the condition (or even by selecting multiple cases from families whilst adjusting for their familial correlation) as they may be more homogeneous in genetic aetiology. This is also known as enrichment sampling 18. However, enrichment sampling does not always increase power in genetic studies (as familial aggregation may also be due to shared environmental factors, or due to genetic variants not under consideration), while general population-based samples can provide more power. If the case definition is a relatively rare sub-phenotype that shows clear segregation in families (and families with multiple affecteds can be collected and genotyped), then a family-based approach will be preferable. A second condition before embarking on a population-based approach is the possibility that one or more of the underlying genetic variants could be common (e.g., with a POPULATION ALLELE FREQUENCY >0.05). Moderately rare (frequency 0.01-0.05) variants can also be detected with available sample sizes but only if they carry a large effect (relative risks > 2.0). If there is an a-priori hypothesis that all undetected genetic variants are rare and of small effect, the samples sizes required to detect such effects in a population-based study will be unfeasibly large 5.
Control selection
A general guide to control selection for any case-control study is that controls should be selected from the same population in which cases arose, and should be representative of the population who would have become cases according to the case definition and recruitment strategies for the study 19. This has long been the golden rule in epidemiological study design, the reason being that it minimises spurious findings (‘false positives’) due to information and selection biases, and CONFOUNDING 20. In genetic association studies, bias due to environmental factors is not generally a problem; the most important type of bias - confounding - is related to the ethnic origin of cases and controls, and is often referred to as POPULATION STRATIFICATION 21. In this situation, a comparison of the frequency of the genetic variant between cases and controls will show a significant difference due to the underlying sampling scheme rather than to a real effect of the variant on disease risk.
The negative effects of population stratification can sometimes be avoided at the study design level (by matching controls to cases on potentially important confounders that mark population structure) or the data analysis level (by adjusting the results for these confounders – see later in this protocol series). It should be noted that matching is only essential when the frequency of the confounder shows such a marked difference between cases and controls that it cannot be adjusted for in the analysis, or in situations where the confounder cannot be accurately measured. ‘Overmatching’ on unnecessary variables will actually reduce power, since all matching variables will need to be taken account of in the analysis 22. Population stratification is minimised when controls are matched to cases on ethnicity (or when cases and controls are restricted to a particular ethnic group), often ascertained through self-description 23, although the extent to which this can avoid stratification depends on the population under study and the differences in disease prevalences and allele frequencies across populations 24-27. Further matching on sex can reduce population stratification in situations where there are gender differences in disease prevalence (since many other traits may be gender-related and may in turn be associated with polymorphisms across the genome). Whether or not further matching on other COVARIATES is necessary and actually reduces the potential of population stratification is a question for debate and will depend on the disease in question. Various epidemiological matching schemes were developed for studies of environmental factors, in which environmental confounding is a problem. Although environmental confounding is not generally considered to be a problem for genetic association studies, theoretically, it could still be an issue in GWA studies of very large sample sizes. One could imagine a scenario where controls were matched to cases on ethnicity and sex, but were very disimilar in terms of e.g. socioeconomic background, smoking patterns etc, resulting in phenotypic differences between cases and controls unrelated to the disease in question, but related to the environmental exposure patterns. These effects could possibly show up in a GWA analysis, although the effects would have to be large and the differential sampling would have to be very pronounced. Considering the current difficulty of finding small genuine effects for complex traits in optimally designed case and control studies, such generating of false positives due to confounding may not be a particular problem in practice, but, with ever increasing sample sizes in future, it may become so.
Any remaining stratification - after careful design of a case-control study - can be investigated and to some extent controlled for by analytical methods 28;29. When a covariate has a marked influence on disease risk but is unlikely to be associated with allele frequency differences (e.g. age), matching may still improve the power of a study by ensuring that controls had the same opportunity as cases to develop - and be diagnosed with - the disease. For example, when controls are selected that are substantially younger than cases, they may include individuals who would have developed the disease of interest given time and thus reduce power.
Whether or not controls should be totally unselected on the basis of other phenotypes (i.e. derived from the general population), or should (also) comprise a mixture of other case groups with unrelated conditions, is currently a matter for debate; it is likely that the optimum solution will vary from one disease to the other. When cases are recruited from clinics, the use of clinic controls diagnosed with other conditions has the advantage of matching for health-seeking and socio-economic characteristics that may be associated with population substructure; however, selective inclusion of other diseases amongst controls has the potential to increase the false positive rate. When centre-based recruitment of controls is not feasible, investigators often use groups of already genotyped ‘common’ controls. In particular, genome-wide association studies (e.g. the Wellcome Trust Case Control Consortium – http://www.wtccc.org.uk/ 14) are likely to use this approach as it is much more economical. It is important that basic characteristics of such panels are known, such as ethnicity, sex, and age, and if possible area of recruitment, so that they can be matched for in the design or adjusted for in analysis. Large-scale biobanking efforts, such as UK Biobank 30, will be able to provide such well-characterised control sets.
It is important to note that the previously described limited matching on - or adjusting for - a few covariates identifying substructure, or indeed the use of common controls, is suitable only for studies which are intended to assess genetic risk. If a future aim is to incorporate environmental risk, or gene-environment interaction, then more stringent design considerations developed to minimise information and selection biases in environmental epidemiological studies need to be applied.
Sample size requirements?
If cases are sampled from all those present in the general population, the relative risks (ODDS RATIOS in a case-control study) for specific alleles influencing complex diseases are expected to be modest to small 31. For polymorphisms with allele frequencies >0.2, the odds ratios are expected be in the range of 1.1-1.5; for allele frequencies between 0.05 and 0.2, up to approximately 3.0. This is true by definition, since a common variant with much larger relative risks would result in a large attributable risk for that variant with respect to the disease; in other words, the variant would explain a very large proportion of the causality of the disease, which would make the condition’s characteristics resemble a Mendelian rather than a complex disorder. As a guideline, sample sizes of at least 1,000 cases and 1,000 controls are required to detect odds ratios around 1.5 in size with at least 80% power, but the required size of each individual study will depend on whether 1) the analysis will also include case sub-groups; 2) the analysis focuses on candidate genes with a limited number of independent tests or genome-wide associations with many thousands of tests; and 3) there is an a-priori hypothesis to be tested relating to a polymorphism of known allele frequency (for example, in a replication study - see below). The expected effect size to be detected in a study (and thus power) can sometimes be increased by using family history enrichment schemes for case sampling 18. However, as mentioned before, they are not guaranteed to do because of environmental and genetic heterogeneity. If recruitment of cases is more difficult than controls, power can often be increased more economically by increasing the ratio of controls to cases 22. When many SNPs are tested, and testing all of these in many thousands of cases and controls become prohibitively expensive, a multi-stage design can be more economical 32. In such a design, all SNPs are tested in a random subset of cases and controls, and those exhibiting a nominal pre-determined significance level are taken through to be tested in the remainder of the study sample. Subsequent analysis needs to be carried out for the different stages combined to maintain power level 33. The optimal multi-stage design depends on the relative cost of stage 1 vs. stage 2 genotyping, but also on the underlying (unknown) disease model, which presents a problem in the design. If budgetary reasons are not a strong issue, one-stage designs are preferred over multi-stage designs. With genotyping costs for whole genome panels ever decreasing, the case for multi-stage designs for budgetary reasons is becoming less strong.
De-novo or a replication study?
Additional considerations need to be taken into account when designing a replication study. Firstly, the effect size found in original studies involving many variants is likely to be biased upwards as it is dependent on reaching statistical significance and being published. This was first described by Beavis 34 in the context of quantitative trait loci, and has since been described in other settings as the ‘Winner’s curse’ 35;36. A study designed to replicate a finding should therefore base sample size calculations on a smaller effect size than found in the original study. Secondly, a comparison has to be made between the origin of the population in which the replication study is conducted, and that of the original study. A true replication study will involve analysis of the same polymorphism in the same direction of effect in the same (ethnic) population measured on the same phenotype as the original study. If another ethnic population is considered, the study is in essence no longer a replication study, since causal pathways and the relative contribution of polymorphism to these pathways may differ between populations. Failure to ‘replicate’ findings in a study of a different population compared to the original study will not allow any meaningful judgement on the validity of result in the original study, but can only provide information on the lack of effect in the second population.
In the following protocol we will go through two hypothetical examples of study design into type 2 diabetes – a candidate gene (CG) study and a genome-wide association (GWA) study.
MATERIALS
Equipment
- Computer workstations with Unix/Linux and Windows operating systems
- Unzipping tool such as Winzip (http://www.winzip.com) or gunzip (http://www.gzip.org)
- Genetic power calculator for one-stage case-control studies 37: http://pngu.mgh.harvard.edu/~purcell/gpc/cc2.html
- Program to calculate the effective number of independent SNPs among a collection of SNPs in LD with each other, SNPSpD 38;39: http://fraser.qimr.edu.au/general/daleN/SNPSpDfraser/
- Program to convert HapMap format files to pedigree and map format files, hap2gold.pl: http://bioinformatics.well.ox.ac.uk/resources.shtml.
- Genetic power calculator for two-stage candidate gene and genome-wide association case-control studies, CaTS 33:http://www.sph.umich.edu/csg/abecasis/CaTS/index.html.
- Files: HapMap genotypic and phenotypic information, to be downloaded from http://www.hapmap.org
PROCEDURE
Specify case definition
- Consider the literature for a consensus definition of the disease of interest. In this search, prioritise standardized and most recent definitions published by relevant organisations, such as the World Health Organisation or recognised disease-specified associations. According to the 2006 American Diabetes Association (ADA) diagnostic criteria 16, diabetes is defined as the presence of impaired glucose tolerance (fasting plasma glucose of ≥ 126 mg/dl or casual plasma glucose of ≥ 200 mg/dl in the presence of symptoms or 2-hr post-load glucose ≥ 200 mg/dl after an oral glucose tolerance test). Type 2 is diagnosed through the exclusion of type 1 and other types of diabetes, and the presence of insulin resistance 16. Following standard diagnostic guidelines allows other groups to more easily replicate initial findings, though it is not always the most powerful approach for initial gene detection.
- If a consensus definition does not exist, consider all evidence and decide on a specific definition that optimises biological and clinical relevance.
- ▲
CRITICAL STEP Keep in mind that vague definitions increase aetiological heterogeneity and decrease the potential of success of your study.
- ▲
- Decide, taking the specificity of the disease definition into account, which setting to use for case identification (sampling frame). Consider that this should provide a population-based cross-section of cases of specified definition, rather than a highly selected sample which may be biased towards unknown characteristics. In choosing the sampling frame, also take into account the additional information that needs to be collected, which should be based on clinical knowledge of the disease and published information about potentially important covariates. Type 2 diabetes cases can be identified from various clinical settings, and cases may vary in clinical/phenotypic characteristics (e.g. ethnicity, age at onset, duration since onset), which could introduce aetiological heterogeneity. In our example, recruited cases will be of Caucasian origin and identified from diabetes clinic(s) which serve the general population. The following information will be collected for phenotypic characterisation and data-analysis: clinic, age, sex, age at symptom onset, age at diagnosis; any relevant clinical/phenotypic covariates (clinical test results; height and weight; family history of metabolic disorders; comorbidity; life-style indicators).
Determine if the disease is heritable
- 4.
Decide from all available evidence in familial aggregation studies, whether there is sufficient evidence that the disease of interest is heritable. Concordance rates of type 2 diabetes in MZ twins have been consistently found to be greater than in DZ twins. Population-based heritability estimates have varied from 26% for type II diabetes (using the type II definition based on fasting plasma glucose levels) to 61% (for type II diabetes + impaired glucose tolerance) 40. In addition, several linkage studies have found suggested chromosomal areas that may harbour predisposing genetic variants 17.- ▲
CRITICAL STEP If the heritability of a disease or sub-phenotype appears to be low (< 20%) and the disease is common, it is likely that very large sample sizes (in excess of 5000 cases and 5000 controls) will be required to find predisposing genetic variants using a population-based approach. Apart from the fact that funds may be better targeted at studying the non-genetic aetiology of such diseases, the sample sizes required may well render the study unfeasible.
- ▲
Is a population-based approach the right choice?
- 5.
Decide, based on all available evidence, whether the aetiology of the disease of interest could reasonably include one or more common underlying polymorphisms (allele frequency > 0.01). This is often difficult to know, but clear criteria against following a population-based approach would be if the disease or subphenotype under study is rare (prevalence < ~ 0.01) and shows clear transmission within families. In our example, it is entirely plausible that one or more common polymorphisms are implicated in the aetiology of type 2 diabetes, as already shown by evidence for the association with PPARγ Pro12Ala (minor allele frequency = 0.15) 41 [NB Other common variants that have been recently identified include TCF7L2 42 and HEXX 13]. The prevalence of all types of diabetes in developed countries was estimated by the WHO at 4.7% in 2000 43, with an estimated 90% comprising type 2 diabetes (a prevalence of 4.2%), making recruitment of large numbers of cases from the general population feasible. - 6.
Decide whether population-based cases can be recruited through a single large centre, or whether a multi-centre approach is needed. When recruitment of several thousands of cases from one centre is difficult (as is often the reality), multi-centre recruitment is required, as long as each collaborator adheres to the agreed phenotypic definition and supplies the agreed covariate information. For our type 2 diabetes example, a multi-clinic national recruitment approach may be fruitful given the sampling requirements.
Control selection
- 7.
Consider the setting(s) from which cases have been recruited, and the population from which these cases are likely to originate. Choose controls in such a away as to maximise the potential for them to have been derived from the same population, and to have had the same potential to be diagnosed as cases. In our example, Caucasian cases have been recruited using a multi-clinic national approach. For CG studies, choose controls as outlined in option A below; for GWA studies follow option B.
OPTION A: Control selection for CG studies
- For the relatively small-scale CG scenario requiring de-novo genotyping, a useful approach is to use classical epidemiological designs of control recruitment tailored to the study 19. In the type 2 diabetes example, we choose Caucasian same-sex friends of cases as controls.
- Collect relevant phenotypic and covariate information for the controls. Although partly disease-specific, these need to include at least 1) demographic data such as age, sex, and region; 2) any relevant symptoms related to the disease; and 3) relevant covariate information. In our diabetes example, we collect information on age, sex, height, weight, diabetic symptoms, other common conditions, and any general covariate information that was collected for cases; if possible, we screen controls for diabetes to increase power (see step 7Bi).
OPTION B: Control selection for GWA studies
- For the large-scale GWA scenario, augment controls by searching for available panels of population-based controls that have already been genotyped genome-wide and for whom basic information is available on ethnicity, age, sex, and geographical area. Ideally, further phenotypic information should be available for such a panel, so as to exclude known cases, and to enable matching of controls to cases on potential confounders (or adjustment in analysis).
- If no such panel is available for the population from which cases were derived, check if there are other epidemiological studies that included population-based controls with phenotypic information for whom DNA may already have been collected.
- If these options are not available, design a tailored control recruitment scheme (similar to step 7A).
- ▲
CRITICAL STEP The potential for the use of common control groups, in particular including case groups with unrelated conditions, is currently a topic of investigation.
- ▲
Determine the required sample size
- 8.
For CG studies: follow option A if distinct SNPs have already been identified that are to be tested directly (i.e. not through LD with another marker), either because of a functional hypothesis or because of prior evidence of association; follow option B if the putative causal variant is not known, but the aim is to find an association through LD with the disease variant. For GWA studies: follow option C.
OPTION A: CG scenario – direct association
- Determine a minimum odds ratio of the disease allele to be detected by the study. As an example, we wish to test the result of PPARγ Pro12Ala 41 through replication. The odds ratio of the disease allele derived from a second, independent, sample in this study was 1.23, with genotypic relative risks of 1.89 (Aa) and 2.20 (AA).
- ▲
CRITICAL STEP If the study aims to replicate a SNP association which has not yet been replicated by others, make sure you use an odds ratio smaller than that from the hypothesis-generating study for the following calculations. How much smaller depends on the size of the original study and whether the initial results suffers from the “Winner’s Curse” 6: if the initial study was small (a few hundred cases & controls), its odds ratio is likely to be more inflated than that from a large study (a few thousand cases & controls).
- ▲
- In the Genetic Power Calculator 37, enter the relevant parameters. Table 1 shows the example for type 2 diabetes/ PPARγ Pro12Ala.
- Tick the box ‘unselected controls’ if a random sample of the population is used who have not been screened for the disease in question.
- Process these parameters. A summary of parameters entered is shown and - at the end - a table is displayed with the number of cases required to detect the effect size specified with 80% power and a variety of TYPE I ERRORS.
Table 1.
Parameter values of the Type 2 Diabetes example as specified in the Genetic Power Calculator 37, following a candidate gene (CG) scenario of direct association.
| Parameter | Value |
|---|---|
| Frequency of the high risk allele | 0.85 |
| Prevalence of disease | 0.042 |
| Genotype relative risks of Aa and AA | 1.89 and 2.20 |
| LD (D’) between tested marker and disease allele* | 1 |
| Marker allele frequency a | 0.85 |
| Minimum number of cases being considered | 1000 |
| Control:case ratio | 1 |
| Box: unselected controls b | unticked |
| Accepted type I error rate | 0.05 |
| Power to detect a true effect | 0.80 |
OPTION B: CG scenario – indirect association with multiple markers
- Consider the total number of markers to be tested in the candidate gene. We select PPARγ (145 kb in size) as a candidate gene, and assume we have previously selected 18 tag SNPs (see supplementary Table 1) from the HapMap on the basis of a minimum pairwise LD of _r2_=0.8 (for details on marker selection see the next paper in this series).
- ▲
CRITICAL STEP If these were 18 independent tests, a simple Bonferroni correction 44 could be applied to calculate the per-SNP p-value deemed significant (0.05/18 = 0.0028). However, some of the SNPs may be in LD with each other, resulting in fewer than 18 independent tests. Using LD information from HapMap, SNPSpD 38 can be used to estimate the number of independent SNPs that they approximate to.
- ▲
- Download the HapMap genotype information for the 18 tag SNPs. Go to HapMart: http://hapmart.hapmap.org/BioMart/martview. Select the most recent NCBI genome build from the Schema drop-down menu. Select the dataset to be used that is closest to your study population. In this example, we select the CEPH population. Click next.
- Among the Filters, tick the option: ‘limit to SNPs with these rsIDs’. Either upload a text file with the rs number of the tag SNPs, or enter the rs numbers in the box provided. Click next.
- In the drop-down menu for Attribute page, select ‘GENOTYPE’. For SNP details, tick the boxes ‘chromosome’, ‘position’ and ‘marker ID’. Under Genotype, tick the box ‘CEU’. Select the output format ‘Text, tab-separated’, and save as a file (here, we specify ‘hapmap18’). Click export.
- ▲
CRITICAL STEP When specifying a file name, do not use an extension (e.g.: .txt), as this will result in the command not being processed in some browsers.
- ▲
- The resulting genotype file will open up in the web browser. Save the file by clicking on ‘Save As’ (in Internet Explorer) or ‘Save Page As’ (in Firefox) in the ‘File’ menu of the browser.
- Download the pedigree information for the HapMap families from: http://www.hapmap.org/downloads/samples_individuals/. For the Caucasian population, download ‘pedinfo2sample_CEU.txt.gz’. Unzip this file using an unzipping utility (e.g. Winzip under Windows; gunzip under Unix/Linux operating systems).
- Convert and recode the downloaded pedigree information and genotype files to generate pedigree and map files in ‘GOLD format’ (for an explanation of this format see: http://www.sph.umich.edu/csg/abecasis/GOLD/docs/formats.html) using the Perl script hap2gold.pl (http://bioinformatics.well.ox.ac.uk/resources.shtml). Download this script to a directory on a Unix/Linux server. In our example, we wish to generate a ped and map file: perl hap2gold.pl –i pedinfo2sample_CEU.txt –p –m hapmap18.txt The pedigree and map output files generated are located in the same directory and called ‘out.pre’ and ‘out.map’.
- Run the files through SNPSpD 38, by going to: http://fraser.qimr.edu.au/general/daleN/SNPSpD/. Scroll down to ‘To run SNPSpD using all fully genotyped family members’. Specify where the ‘.pre’ and ‘.map’ files are located by browsing to the relevant directories. Click submit query. The results page starts with a matrix of pair-wise LD measures for the tag SNPs. In our example, the 18 SNPs represent 15.87 effective independent marker (Meff) loci calculated using Nyholt’s approach 38. The MeffLi calculated using an alternative approach by Li and Ji 39 is 11.06, with an associated per-SNP significance threshold (after applying a Bonferroni correction 44) of 0.05/11.06 = 0.0046.
- ▲
CRITICAL STEP The MeffLi is more accurate than the Nyholt’s Meff when SNPs are moderately correlated, such as in a tag SNP set, though no method is currently accepted as accurately reflecting the correlation structure for all scenarios.
- ▲
- Enter this new type I error rate in the Genetic Power Calculator 37 as described above. Vary the parameter values for disease allele frequency to observe the effect on required sample size.
- ▲
CRITICAL STEP In view of the fact the study design involves common variants underlying a common complex disease, the suggested range of parameter values for disease allele frequency is 0.05 ≤ freq ≤ 0.95; for genotype relative risks (GRRs) it is 1.10 ≤ GRR ≤ 2.00.
- ▲
- Since the causal variant is more likely to be in LD with the tag SNP set (rather than a member of it), the required number of cases and controls needs to be adjusted for the mean pairwise r2 45. Divide the number of cases and controls by the estimated mean correlation between tagged and untagged common variation 3;46. For Caucasians, this is 0.97.
- ▲
CRITICAL STEP Instead of using the mean r2 value between tag SNPs and all common variation, also use the minimum r2 value of 0.8. This will show how to capture a small but potentially important extra proportion of common SNPs that are in a lower average LD (0.8 ≤ r2 ≤ 0.97) with other common SNPs, at the price of a more substantial increase in sample size.
OPTION C: GWA scenario (one or two-stage)
- Assume that the SNPs on the selected GWA panel are independent of each other. For our GWA example, we assume an array of ~ 500,000 tagSNPs has been selected.
- Based on budget restrictions, make an initial estimate of the minimum number of cases and controls given genotyping costs, assuming that everyone will be genotyped on the genome-wide array (one-stage study). In our example, we start by planning to collect 1000 type 2 diabetes cases and 1000 controls.
- Assume different parameter values for both disease allele frequency and genotype relative risks in the following calculations. Start up CaTS. Under Sample Size, enter the numbers of cases and controls. Under Two Stage Design, leave the percentages genotyped in stages 1 and 2 for the moment, and enter the SNP-based significance value assuming 500,000 independent tests and a global false positive rate of 0.05 after Bonferroni correction. This significance value is 0.05/500,000 = 0.0000001 (= 1× 10−7). Under Disease Model, enter the population prevalence of type 2 diabetes: 0.042. Vary disease allele frequency, genotype relative risk, and genetic model to desired specifications. Select the ‘Power’ tab at the bottom of the page to view the power of detection of the disease allele in a one-stage study. Move the slides for number of cases and controls to obtain the sample sizes required to detect the specified disease allele frequency and GRR combinations at a power of 80%.
- ▲
CRITICAL STEP As before, in view of the fact that the study design involves common variants underlying a common complex disease, the suggested range of parameter values for disease allele frequency is 0.05 ≤ freq ≤ 0.95; for GRRs it is 1.10 ≤ GRR ≤ 2.00.
- ▲
- When arriving at the desired sample size, divide the total number of cases and controls by the estimated mean or minimum r2 between the SNP panel and all common variation (~0.97) 46 to allow for LD between tag SNP and untyped disease variant.
- To view the potential cost saving in a two-stage design in CaTS, first specify the parameter values selected for the one-stage design. Choose the ‘Optimization’ tab. Specify the per genotype cost ratio of stage 2: stage 1, and the target power (80%). The results will show what percentage of total cost of a one-stage study can be saved by genotyping?% of individuals in stage 1, and following up?% markers in the remainder of the sample in stage 2.
- ▲
CRITICAL STEP Vary the parameter specifications for disease allele frequency and GRR and re-optimize to see how the optimal design varies with different model specifications. Consider also the situation in which 500,000 tag SNPs on the panel are not independent, but translate into an effective number of e.g. 300,000 independent tag SNPs.
- ▲
TIMING
None of the programmes described take longer than a few seconds to run. Thinking through the designs and iterating through the many different parameters in the disease models are the rate-limiting steps.
? TROUBLESHOOTING
For help on the programmes used in this protocol, please refer to the relevant websites.
Step 8Bvii
Explanation of hap2gold.pl is provided when typing: perl hap2gold.pl –h.
Step 8Ciii and v
When using CaTS to find the optimal two-stage design, make sure the disease model is specified in such a way that the target power for the two-stage design is less than or equal to the power in the one-stage design. If a one-stage design is selected that provides 80% power, optimizing the two-stage design may produce a message indicating that ‘The requested power cannot be achieved for your sample size and disease model’. This is because the one-stage power has been rounded to 80% but is in fact slightly lower. Relaxing your model parameters slightly whilst maintaining a one-stage rounded 80% power value should solve the problem.
ANTICIPATED RESULTS
Sample size calculations
CG scenario – direct association (step 8A)
In our type 2 diabetes example, entering the parameter values specified (Table 1) into the Genetic Power Calculator shows we need 1470 cases & 1470 controls. Choosing three controls per case changes the required numbers to 1017 cases and 3051 controls. Not screening controls for diabetes increases the figures to 1104 cases and 3312 controls.
CG scenario – indirect association (step 8B)
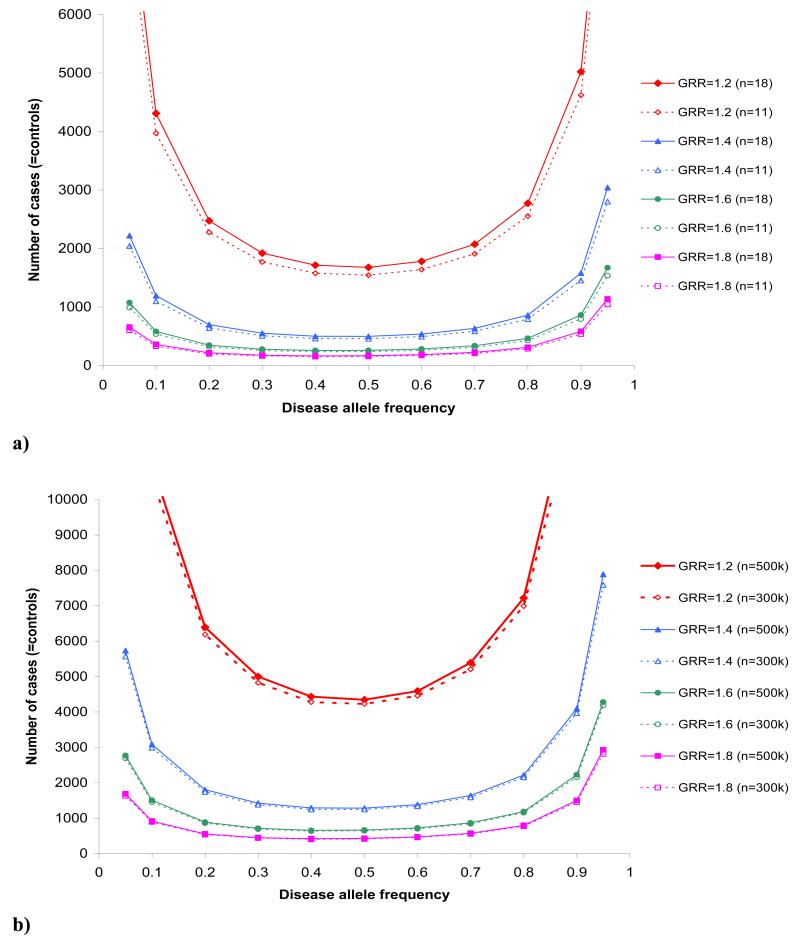
Using the same parameter values as specified in the direct scenario (Table 1), but allowing for 18 SNPs tested (per-SNP significance threshold p=0.0028) increases the required number to 2749 cases and 2749 controls in the Genetic Power Calculator. Reducing the number of independent tests based on the SNP results to 11 independent tag SNPs (per-SNP significance threshold p=0.0046), reduces the required number of cases and controls to 2531 of each. This result assumes that the disease SNP was among the tag SNPs. After allowing for a mean r2 of 0.97 between tag SNPs, we need approximately 2609 cases and 2609 controls (using a minimum r2 value of 0.8 increases this to 3164 cases and 3164 controls). Figure 1a shows the required number of cases (assuming a control:case ratio of 1:1 and an r2 correction of 0.97) for different options of disease allele frequency and GRRs, under a multiplicative disease model (GRRAA=(GRR)Aa2), that achieve 80% power of detection with SNP-based significance thresholds of p=0.0028 (18 SNPs) and p=0.0046 (11 SNPs), respectively.
Fig 1.
Required number of cases (=number of controls) to detect varying disease allele frequencies and GRRs with 80% power in a) a CG scenario with indirect association assuming either 18 independent tagSNPs (solid lines; per-SNP type I error rate = 0.0028) or 11 independent tagSNPs (dashed lines; per-SNP type I error rate = 0.0046) and b) a GWA scenario assuming either 500,000 independent tagSNPs (solid lines; per-SNP type I error rate= 1×10−7) or 300,000 independent tag SNPs (dashed lines; per-SNP type I error rate= 1.67×10−7). A multiplicative model was assumed (GRRAA = (GRRAa2)) and numbers were adjusted for a mean r2 of 0.97 (Caucasians) between a common tagSNP and common disease allele.
GWA scenario (step 8C)
Using our type 2 diabetes example in CaTS, Figure 1b shows the sample sizes required, in a one-stage design, to detect different combinations of disease allele frequency and GRRs with 80% power, assuming a SNP-based significance threshold of 1 × 10−7 (using a Bonferroni correction for all 500,000 tagSNPs on the panel) and of 1.67 × 10−7 (when assuming that 500,000 tagSNPs on the panel correspond to 300,000 effective independent SNPs). A control:case ratio of 1:1 and a multiplicative disease model (GRRAA=(GRR)Aa2) were assumed.
To demonstrate potential cost savings adopting a two-stage design, we first assume a minimum sample size for a one-stage design into type 2 diabetes, i.e. 3000 cases and 3000 controls. Table 2 shows how the different optimal designs for a two-stage study depend on disease allele frequency and GRR.
Table 2.
Optimal designs calculated using CaTS 33for a two-stage study with 80% power for a total sample size of 3000 cases and 3000 controls, by varying disease allele frequency and genotype relative risk (GRR). a
| Disease allele frequency | GRRAa * | % of total sample size genotyped in stage 1 | % of markers genotyped in stage 2 | % cost saving compared to one-stage design |
|---|---|---|---|---|
| 0.05 | 1.56317 | 68.96 | 1.22 | 27.25 |
| 0.1 | 1.39913 | 68.14 | 1.51 | 27.04 |
| 0.3 | 1.25881 | 64.94 | 1.61 | 29.41 |
| 0.5 | 1.24121 | 63.73 | 1.32 | 31.49 |
| 0.7 | 1.27357 | 65.45 | 1.42 | 29.66 |
| 0.9 | 1.47863 | 67.25 | 1.42 | 28.11 |
Supplementary Material
Supplementary Table
ACKNOWLEDGMENTS
We thank David Evans and John Broxholme for their help with perl scripting. This work was supported by funding from the European Union (MolPAGE grant LSHG-512066) to KTZ and from the Wellcome Trust to LRC
Footnotes
COMPETING INTERESTS STATEMENTS: The authors declare no competing financial interests.
References
- 1.Gilliam TC, et al. Localization of the Huntington’s disease gene to a small segment of chromosome 4 flanked by D4S10 and the telomere. Cell. 1987;50:565–71. doi: 10.1016/0092-8674(87)90029-8. [DOI] [PubMed] [Google Scholar]
- 2.Kerem B, et al. Identification of the cystic fibrosis gene: genetic analysis. Science. 1989;245:1073–80. doi: 10.1126/science.2570460. [DOI] [PubMed] [Google Scholar]
- 3.The International HapMap Consortium A haplotype map of the human genome. Nature. 2005;437:1299–320. doi: 10.1038/nature04226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Palmer LJ, Cardon LR. Shaking the tree: mapping complex disease genes with linkage disequilibrium. Lancet. 2005;366:1223–34. doi: 10.1016/S0140-6736(05)67485-5. [DOI] [PubMed] [Google Scholar]
- 5.Zondervan KT, Cardon LR. The complex interplay among factors that influence allelic association. Nat Rev Genet. 2004;5:89–100. doi: 10.1038/nrg1270. [DOI] [PubMed] [Google Scholar]
- 6.Hirschhorn JN, Lohmueller K, Byrne E, Hirschhorn K. A comprehensive review of genetic association studies. Genet Med. 2002;4:45–61. doi: 10.1097/00125817-200203000-00002. [DOI] [PubMed] [Google Scholar]
- 7.Weiss KM, Terwilliger JD. How many diseases does it take to map a gene with SNPs? Nat Genet. 2000;26:151–7. doi: 10.1038/79866. [DOI] [PubMed] [Google Scholar]
- 8.Klein RJ, et al. Complement factor H polymorphism in age-related macular degeneration. Science. 2005;308:385–9. doi: 10.1126/science.1109557. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Dewan A, et al. HTRA1 promoter polymorphism in wet age-related macular degeneration. Science. 2006;314:989–92. doi: 10.1126/science.1133807. [DOI] [PubMed] [Google Scholar]
- 10.Duerr RH, et al. A Genome-Wide Association Study Identifies IL23R as an Inflammatory Bowel Disease Gene. Science. 2006;314:1461–3. doi: 10.1126/science.1135245. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Cardon LR. Genetics. Delivering new disease genes. Science. 2006;314:1403–5. doi: 10.1126/science.1136668. [DOI] [PubMed] [Google Scholar]
- 12.Sladek R, et al. A genome-wide association study identifies novel risk loci for type 2 diabetes. Nature. 2007;445:881–5. doi: 10.1038/nature05616. [DOI] [PubMed] [Google Scholar]
- 13.Frayling TM, et al. A Common Variant in the FTO Gene Is Associated with Body Mass Index and Predisposes to Childhood and Adult Obesity. Science. 2007;316:889–94. doi: 10.1126/science.1141634. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.The Wellcome Trust Case Control Consortium Genome-wide association study of 14,000 cases of seven common diseases and 3,000 shared controls. Nature. 2007;447:661–78. doi: 10.1038/nature05911. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Bennett PH. Basis of the present classification of diabetes. Adv Exp Med Biol. 1985;189:17–29. doi: 10.1007/978-1-4757-1850-8_2. [DOI] [PubMed] [Google Scholar]
- 16.American Diabetes Association Diagnosis and classification of diabetes mellitus. Diabetes Care. 2006;29:S43–S48. [PubMed] [Google Scholar]
- 17.O’Rahilly S, Barroso I, Wareham NJ. Genetic factors in type 2 diabetes: the end of the beginning? Science. 2005;307:370–3. doi: 10.1126/science.1104346. [DOI] [PubMed] [Google Scholar]
- 18.Antoniou AC, Easton DF. Polygenic inheritance of breast cancer: Implications for design of association studies. Genet Epidemiol. 2003;25:190–202. doi: 10.1002/gepi.10261. [DOI] [PubMed] [Google Scholar]
- 19.Rothman KJ, Greenland S. Case-control studies. In: Rothman KJ, Greenland S, editors. Modern Epidemiology. Lippincott-Raven; Philadelphia: 1998. pp. 93–114. [Google Scholar]
- 20.Rothman KJ, Greenland S. Precision and validity in epidemiologic studies. In: Rothman KJ, Greenland SG, editors. Modern epidemiology. Lippincott-Raven; Philadelphia: 1998. pp. 115–134. [Google Scholar]
- 21.Cardon LR, Palmer LJ. Population stratification and spurious allelic association. Lancet. 2003;361:598–604. doi: 10.1016/S0140-6736(03)12520-2. [DOI] [PubMed] [Google Scholar]
- 22.Schlesselman JJ. Case-control studies: design, conduct and analysis. Oxford University Press; Oxford: 1982. pp. 1–330. [Google Scholar]
- 23.Tang H, et al. Genetic structure, self-identified race/ethnicity, and confounding in case-control association studies. Am J Hum Genet. 2005;76:268–75. doi: 10.1086/427888. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Campbell CD, et al. Demonstrating stratification in a European American population. Nat Genet. 2005;37:868–72. doi: 10.1038/ng1607. [DOI] [PubMed] [Google Scholar]
- 25.Marchini J, Cardon LR, Phillips MS, Donnelly P. The effects of human population structure on large genetic association studies. Nat Genet. 2004;36:512–7. doi: 10.1038/ng1337. [DOI] [PubMed] [Google Scholar]
- 26.Helgason A, et al. An Icelandic example of the impact of population structure on association studies. Nat Genet. 2005;37:90–5. doi: 10.1038/ng1492. [DOI] [PubMed] [Google Scholar]
- 27.Steffens M, et al. SNP-based analysis of genetic substructure in the German population. Hum Hered. 2006;62:20–9. doi: 10.1159/000095850. [DOI] [PubMed] [Google Scholar]
- 28.Tsai HJ, et al. Comparison of three methods to estimate genetic ancestry and control for stratification in genetic association studies among admixed populations. Hum Genet. 2005;118:424–33. doi: 10.1007/s00439-005-0067-z. [DOI] [PubMed] [Google Scholar]
- 29.Gorroochurn P, Heiman GA, Hodge SE, Greenberg DA. Centralizing the non-central chi-square: A new method to correct for population stratification in genetic case-control association studies. Genet Epidemiol. 2006;30:277–89. doi: 10.1002/gepi.20143. [DOI] [PubMed] [Google Scholar]
- 30.Palmer LJ. UK Biobank: bank on it. Lancet. 2007;369:1980–2. doi: 10.1016/S0140-6736(07)60924-6. [DOI] [PubMed] [Google Scholar]
- 31.Cardon LR, Bell JI. Association study designs for complex diseases. Nat Rev Genet. 2001;2:91–9. doi: 10.1038/35052543. [DOI] [PubMed] [Google Scholar]
- 32.Thomas D, Xie R, Gebregziabher M. Two-Stage sampling designs for gene association studies. Genet Epidemiol. 2004;27:401–14. doi: 10.1002/gepi.20047. [DOI] [PubMed] [Google Scholar]
- 33.Skol AD, Scott LJ, Abecasis GR, Boehnke M. Joint analysis is more efficient than replication-based analysis for two-stage genome-wide association studies. Nat Genet. 2006;38:209–13. doi: 10.1038/ng1706. [DOI] [PubMed] [Google Scholar]
- 34.Beavis WD. The power and deceit of QTL experiments: lessons from comparative QTL studies; Proceedings of the Forty-Ninth Annual Corn & Sorghum Industry Research Conference; American Trade Association, Washington DC. 1994. pp. 250–266. [Google Scholar]
- 35.Lohmueller KE, et al. Meta-analysis of genetic association studies supports a contribution of common variants to susceptibility to common disease. Nat Genet. 2003;33:177–82. doi: 10.1038/ng1071. [DOI] [PubMed] [Google Scholar]
- 36.Garner C. Upward bias in odds ratio estimates from genome-wide association studies. Genet Epidemiol. 2007;31:288–95. doi: 10.1002/gepi.20209. [DOI] [PubMed] [Google Scholar]
- 37.Purcell S, Cherny SS, Sham PC. Genetic Power Calculator: design of linkage and association genetic mapping studies of complex traits. Bioinformatics. 2003;19:149–50. doi: 10.1093/bioinformatics/19.1.149. [DOI] [PubMed] [Google Scholar]
- 38.Nyholt DR. A simple correction for multiple testing for single-nucleotide polymorphisms in linkage disequilibrium with each other. Am J Hum Genet. 2004;74:765–9. doi: 10.1086/383251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Li J, Ji L. Adjusting multiple testing in multilocus analyses using the eigenvalues of a correlation matrix. Heredity. 2005;95:221–7. doi: 10.1038/sj.hdy.6800717. [DOI] [PubMed] [Google Scholar]
- 40.Poulsen P, Kyvik KO, Vaag A, Beck-Nielsen H. Heritability of type II (non-insulin-dependent) diabetes mellitus and abnormal glucose tolerance--a population-based twin study. Diabetologia. 1999;42:139–45. doi: 10.1007/s001250051131. [DOI] [PubMed] [Google Scholar]
- 41.Altshuler D, et al. The common PPARgamma Pro12Ala polymorphism is associated with decreased risk of type 2 diabetes. Nat Genet. 2000;26:76–80. doi: 10.1038/79216. [DOI] [PubMed] [Google Scholar]
- 42.Grant SF, et al. Variant of transcription factor 7-like 2 (TCF7L2) gene confers risk of type 2 diabetes. Nat Genet. 2006;38:320–3. doi: 10.1038/ng1732. [DOI] [PubMed] [Google Scholar]
- 43.Wild S, et al. Global prevalence of diabetes: estimates for the year 2000 and projections for 2030. Diabetes Care. 2004;27:1047–53. doi: 10.2337/diacare.27.5.1047. [DOI] [PubMed] [Google Scholar]
- 44.Bland JM, Altman DG. Multiple significance tests: the Bonferroni method. BMJ. 1995;310:170. doi: 10.1136/bmj.310.6973.170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Kruglyak L. Prospects for whole-genome linkage disequilibrium mapping of common disease genes. Nat Genet. 1999;22:139–44. doi: 10.1038/9642. [DOI] [PubMed] [Google Scholar]
- 46.Barrett JC, Cardon LR. Evaluating coverage of genome-wide association studies. Nat Genet. 2006;38:659–62. doi: 10.1038/ng1801. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Table