A light-dependent magnetoreception mechanism insensitive to light intensity and polarization (original) (raw)
Abstract
Billions of migratory birds navigate thousands of kilometres every year aided by a magnetic compass sense, the biophysical mechanism of which is unclear. One leading hypothesis is that absorption of light by specialized photoreceptors in the retina produces short-lived chemical intermediates known as radical pairs whose chemistry is sensitive to tiny magnetic interactions. A potentially serious but largely ignored obstacle to this theory is how directional information derived from the Earth's magnetic field can be separated from the much stronger variations in the intensity and polarization of the incident light. Here we propose a simple solution in which these extraneous effects are cancelled by taking the ratio of the signals from two neighbouring populations of magnetoreceptors. Geometric and biological arguments are used to derive a set of conditions that make this possible. We argue that one likely location of the magnetoreceptor molecules would be in association with ordered opsin dimers in the membrane discs of the outer segments of double-cone photoreceptor cells.
Keywords: magnetoreception, radical pair mechanism, light polarization, photoselection, double-cone photoreceptor cells, opsin dimers
1. Introduction
The radical pair mechanism currently offers the most promising explanation for the astounding ability of migratory birds to sense the direction of the Earth's magnetic field. It proposes that the field is detected via its influence on the coherent spin dynamics of a short-lived, photo-induced radical pair reaction intermediate [1–3]. At present the most likely candidate molecule is the blue-light photoreceptor, cryptochrome, in which a flavin radical and a tryptophan radical are formed photochemically [4–8]. A signalling state is assumed to be produced from the radical pair state with a quantum yield that depends on the direction of the magnetic field with respect to an alignment axis of the protein molecules in the bird's body. Support for this proposition includes the observations that the compass requires blue-green light to function [9,10], that it detects the axis rather than the polarity of the magnetic field [11], that the photochemistry of isolated cryptochromes in vitro is magnetically sensitive [12], that magnetic compass information is processed in visual brain areas [13,14], that radiofrequency electromagnetic fields can disrupt birds' magnetic orientation [15–18], and that magnetic behavioural responses in Drosophila can be abolished by suppressing cryptochrome expression [19–26]. There is strong evidence that the magnetoreceptors are located in the bird's retinas, where various cell types are known to contain cryptochromes [3,27–30].
The strength of the signal produced by a population of aligned magnetoreceptor molecules (e.g. the cryptochromes in a single cell) in response to a magnetic stimulus depends not only on the direction and intensity of the magnetic field but also on the number of radical pairs responsible for the signal. The fact that the radical pairs are created photochemically means that changes in light intensity would affect the output of a single cell in a manner that would be indistinguishable from a change in the direction of the magnetic field experienced by the cell. This can be understood by considering a simple example. Suppose that when a field is applied in one direction, 10% of the radical pairs in a single receptor cell react to form the signalling state and that when the field is applied in a perpendicular direction, 20% of radical pairs end up in the signalling state. If the incident light entering the receptor cells excites 100 cryptochrome molecules to produce 100 radical pairs, there will be 10 molecules of signalling state produced when the field is in direction 1 and 20 when the field is in direction 2. Now suppose that the cell is exposed to more intense light, such that 200 cryptochrome molecules are excited to produce 200 radical pairs. When the field is in direction 1, 20 molecules of signalling state will be produced, exactly the same as if the field were in direction 2 under the lower light intensity.
It is worth noting that this argument applies even if the magnetically sensitive radical pair is produced in a light-independent reaction subsequent to the initial photoexcitation, as has been suggested in a recent study [31]. The number of radical pairs (and hence of signalling state molecules) depends on the concentration of the photochemically produced precursor state and therefore still depends on the number of photons absorbed.
A closely related problem is encountered in colour vision, where a single photoreceptor cell cannot distinguish a change in colour (increased intensity at some wavelengths at the expense of others) from a change in brightness (a uniform increase of intensity across all wavelengths). The problem is resolved by detecting the relative stimulation of neighbouring photoreceptor cells containing pigments tuned to different wavelengths [32]. Thus, the retina is capable of integrating signals from neighbouring photoreceptor cells. Such integration can be achieved either through horizontal cell inhibition and/or by bi-stratified ganglion cells connecting to on- and off-bipolar cells. It has recently been suggested that magnetic sensing could work in a similar fashion, by detecting the ratio of signals from neighbouring receptor cells that have different orientations within the retina and hence different magnetic responses (see fig. 9 in ref. [3]). Double-cone photoreceptor cells, the most common cone type in the avian retina [33], seem particularly appealing in this context: the two member-cones would be exposed to very similar light intensities and could house populations of magnetoreceptor molecules with well-defined orientations [3].
Although comparing the signals generated by two populations of ordered magnetoreceptor molecules seems an obvious and elegant solution to the light-intensity problem, it raises questions about the effect of linearly polarized light on the operation of the compass sensor. The probability that a molecule absorbs a photon depends on the orientation of its transition dipole moment relative to the electric vector of the light, with maximum absorption occurring when the two vectors are parallel and no absorption when they are perpendicular, an effect known as photoselection [34]. Vertebrate rod and cone cells are normally insensitive to polarization because the opsin photoreceptor proteins in the membrane discs are free to rotate around the direction of the incoming light, so that, taken together, the opsins within a photoreceptor cell absorb all polarizations of light with equal probability [35,36]. Aligned populations of magnetoreceptors will, however, preferentially absorb light of a particular polarization, i.e. a particular direction of the electric vector [37].
Skylight is naturally polarized by scattering from molecules and particles in the Earth's atmosphere [38,39]. The degree and axis of the polarization depend on the direction of observation relative to the light source, which can be the sun or the moon [40,41]. This variation means that aligned receptors receiving light from different regions of the sky will absorb different numbers of photons and hence produce different numbers of radical pairs. The attendant changes in the yield of the signalling state could easily swamp the much smaller variations produced by the magnetic field (estimated at 1% or less) [42,43] in a similar way to changes in light intensity. Muheim et al. have suggested that polarized light may indeed alter a bird's perception of the magnetic field [44].
We argue here that there is a way in which the strong effects of light intensity and polarization can simultaneously be prevented from obscuring the weak directional information available from the magnetic field by using the ratio of the outputs from two neighbouring populations of magnetoreceptors. We use geometric arguments to derive a set of conditions under which this is possible and propose how they could be realized in cells in the retina.
2. Results
If the ratio of signals from two adjacent cells, A and B, in the retina is to contain only information about the magnetic field, then light-induced radical pairs must be formed with identical probability in the two cells but the magnetic field effects on the receptors in A and B must differ. This imposes certain constraints on the orientations of the magnetoreceptor molecules within the cells and the cells within the retina, which we now derive using simple geometric and biological arguments.
2.1. Geometric requirements: relative orientation of magnetoreceptor cells
We start with no preconceptions about the orientations of the magnetoreceptors or the cells that contain them, and make three assumptions: first, that the two cells, side-by-side in the retina, receive equal numbers of photons per second, and, second, that the orientations of the magnetoreceptor molecules contained in each cell are identical. The only difference between the two cells is that one is rotated relative to the other by an angle, and around an axis, to be determined.
Note that we do not need to assume that the cells contain equal numbers of photoreceptor molecules. For example, if cell A contains twice as many photoreceptors as cell B, the probability of a photon being absorbed will always be twice as high in cell A compared to cell B, regardless of changes in light intensity or polarization. Therefore, the ratio of signals A/B will be multiplied by a constant factor of 2. The important thing is that the probability per photoreceptor of absorbing a photon is identical in the two cells. However, for simplicity, equal numbers of photoreceptor molecules in each cell are assumed for all the simulations presented here.
The third assumption is that the magnetoreceptor molecules have perfect rotational order within the cells. The eye is imagined to operate as a pinhole camera. Rays of light are assumed to enter the eye via the pinhole (the pupil) and to strike the retina at a position determined simply by their direction, without refraction or scattering.
To convert identical numbers of cryptochromes from the resting state to the radical pair state, the probability of photon absorption by the flavin chromophores should be the same in the two cells. The absorption probability is proportional to cos2_ω_, where ω is the angle (0 ≤ ω < 180°) between the transition dipole moment (TDM) of the flavin and the electric vector of the incoming light, e [34]. (Vector quantities are written in bold face.) For 100% linearly polarized light, e has a unique orientation in the plane perpendicular to the light-propagation direction, v, whereas for unpolarized light all orientations of e perpendicular to v occur with equal probability. In cryptochrome, the TDM lies approximately parallel to the long in-plane axis of the isoalloxazine ring system of the flavin chromophore, labelled _y_m in figure 1a [34,45,46].
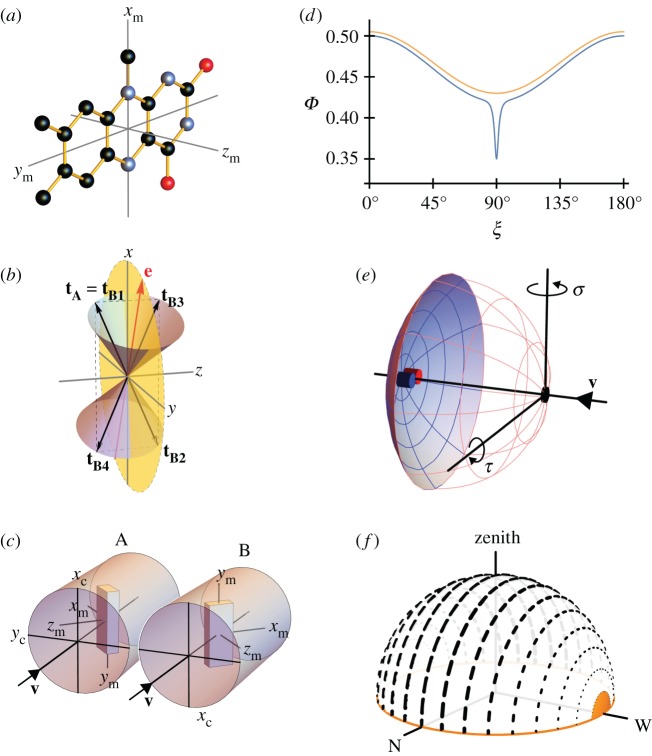
Figure 1.
(a) Structure of the tricyclic flavin component of the flavin adenine dinucleotide chromophore in cryptochrome including the molecular axis system, (_x_m, _y_m, _z_m), used in the text. The transition dipole moment is approximately parallel to _y_m, the long, in-plane axis of the aromatic ring system. The approximate symmetry axis of the magnetic response of a flavin-containing radical pair is parallel to _z_m. Black, blue and red balls indicate carbon, nitrogen and oxygen atoms. Hydrogen atoms are not shown. (b) Representation of the transition dipole moment vectors in equations (2.1), (2.2) and (2.4). The incoming light propagates along the _z_-axis. e is an arbitrarily chosen electric vector (red) in the xy_-plane (yellow) and is the axis of the two cones. tA is the TDM of an arbitrarily oriented magnetoreceptor molecule in cell A. For the particular e-vector shown in the figure, any molecule in cell B whose TDM vector points from the origin to any point on the surface of one of the two cones has the same probability of absorbing a photon as does the molecule whose TDM vector is tA (because all such vectors have the same value of cos2_ω (equation (2.3)). However, only four of these vectors, tB1, tB2, tB3 and tB4 (all in the xz plane) give the same probability of photon absorption as tA for any direction of e in the xy plane. tB1 is identical to tA. tB2 = −tB1 (i.e. tB1 exactly inverted). tB3 and tB4 are, respectively, the reflections of tB1 and tB2 in the xy plane. Only tB4 is related to tA by a rotation around the _z_-axis. (c) Schematic representation of two adjacent cylindrical photoreceptor cells, A and B, in the retina. The direction of propagation of the incoming light, v, is parallel to _z_c, the long symmetry axis of the cells. A and B are identical apart from a 180° rotation around v. Both cells are considered to contain populations of aligned flavin chromophores, one of which is shown in each cell as a cuboid with approximately the same aspect ratios as the flavin structure in (a). The TDM vectors (_y_m) are parallel in A and B and both are perpendicular to _z_c. The magnetic symmetry axes (_z_m) are at 65° to _z_c and lie in the _y_c_z_c-plane. (d) Idealized orientation-dependence of the yield of the signalling state of cryptochrome formed from the flavin–tryptophan radical pair state of the protein. Φ(ξ) is modelled (equation (2.5)) so as to resemble the results of calculations presented in Ref. [47] using _a_0 = 0.5, _a_1 = −0.08, _a_128 = −0.01, _a_512 = −0.03, _a_2048 = −0.03. ξ is the angle between the magnetic field axis and the _z_m axis of the flavin structure shown in (a). The orange and blue traces are appropriate for radical pairs with short and long lifetimes, respectively. The former, which includes just the _a_0 and _a_1 terms, has been shifted vertically by +0.015 for clarity. (e) Schematic representation of an eye. Cells A and B (small blue and red cylinders) are positioned at the centre of the retina (pink/blue spherical section), diametrically opposite the pupil (black spot). The magnetic responses of A and B are calculated for different ‘lines of sight’ of the eye, obtained by rotating the eye around the indicated axes. σ and τ are the yaw and pitch angles, respectively. (f) Representation of skylight polarization according to the Rayleigh sky model when the sun is on the horizon (orange) in the west. The directions and weights of the short black lines represent the e-vectors of light perceived by an observer at the centre of the celestial hemisphere.
The rotation that relates the orientations of the two cells will, in general, change the orientation of the TDMs in A and B relative to e. If the chromophores in A and B are to have the same probability of absorbing a photon, we must have 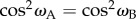 , i.e. either _ω_A = _ω_B or _ω_A = 180° − ω_B. For the separation mechanism to work for all possible polarizations, the cell rotation needs to preserve cos2_ω for an e-vector with an arbitrary direction in the plane perpendicular to v. The conditions for this to occur can be deduced using elementary vector algebra. In the following, vectors are written in terms of their projections (e.g. px, py, pz) onto three orthogonal axes (x, y, z, respectively). Thus, a general vector, p, is written
, i.e. either _ω_A = _ω_B or _ω_A = 180° − ω_B. For the separation mechanism to work for all possible polarizations, the cell rotation needs to preserve cos2_ω for an e-vector with an arbitrary direction in the plane perpendicular to v. The conditions for this to occur can be deduced using elementary vector algebra. In the following, vectors are written in terms of their projections (e.g. px, py, pz) onto three orthogonal axes (x, y, z, respectively). Thus, a general vector, p, is written 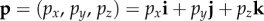 where i, j and k are unit vectors along the x, y and z axes, respectively. Note that the scalar product of two vectors p and q is defined by
where i, j and k are unit vectors along the x, y and z axes, respectively. Note that the scalar product of two vectors p and q is defined by  and that the scalar product of two unit vectors is equal to the cosine of the angle between them.
and that the scalar product of two unit vectors is equal to the cosine of the angle between them.
Taking v as the _z_-axis, the unit vector that represents the polarization must lie in the _xy_-plane and has the general form:
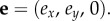 |
2.1 |
|---|
If the TDM of the receptor molecules in cell A is defined, without loss of generality, by the unit vector
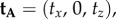 |
2.2 |
|---|
then cos2_ω_A is equal to the square of the scalar product of vectors e and tA:
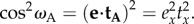 |
2.3 |
|---|
For the particular e-vector shown in figure 1b, a molecule in cell B whose TDM vector points from the origin to any point on the surface of one of the two cones satisfies 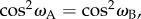 i.e. has the same probability of absorbing a photon as does the molecule whose TDM vector is tA. However, only the four vectors in equation (2.4) give the same probability of photon absorption as does tA for any direction of e in the xy plane (i.e. any polarization of the light):
i.e. has the same probability of absorbing a photon as does the molecule whose TDM vector is tA. However, only the four vectors in equation (2.4) give the same probability of photon absorption as does tA for any direction of e in the xy plane (i.e. any polarization of the light):
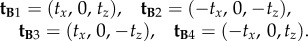 |
2.4 |
|---|
That is, the rotation that relates A and B must either invert the _x_-component or the _z_-component of the TDM or invert both or leave both unchanged.
The next stage is to use biological arguments to eliminate three of the four TDM orientations in equation (2.4). The most probable location of the magnetoreceptors is inside rod or cone photoreceptor cells [3]. Cryptochromes have been found in several types of photoreceptor cells [27,29], and of all the cells in the retina the photoreceptors are the only ones known to contain multiple highly ordered structures—the membrane discs—that could provide an ideal scaffold for aligning and immobilizing magnetoreceptor molecules [48]. Both rod and cone photoreceptors are roughly pencil-shaped [49] with approximate cylindrical symmetry; they connect to the layer of horizontal and bipolar cells at one end and to the pigment epithelium at the other. It therefore seems most likely that the A ↔ B rotation would be around the long symmetry axis of the cell which, in vertebrate eyes, points directly at the pupil irrespective of the cell's position in the retina [50–53]. We therefore infer that the A ↔ B rotation should be around the direction of the incoming light, v, (defined above as the _z_-axis) in our pinhole-camera eye.
Returning to equation (2.4), this conclusion immediately excludes 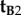 and
and 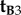 because a _z_-rotation of a vector leaves its _z_-component unchanged.
because a _z_-rotation of a vector leaves its _z_-component unchanged. 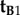 , which is identical to
, which is identical to 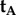 , may also be ruled out on the basis that the TDM would have to be parallel to the rotation axis (i.e. v) in which case cos2_ω_A and cos2_ω_B would both equal zero (equation (2.3)) and no light would be absorbed by the magnetoreceptors in either cell. Thus (figure 1c), we are left with
, may also be ruled out on the basis that the TDM would have to be parallel to the rotation axis (i.e. v) in which case cos2_ω_A and cos2_ω_B would both equal zero (equation (2.3)) and no light would be absorbed by the magnetoreceptors in either cell. Thus (figure 1c), we are left with 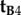 . Because
. Because 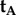 and
and 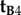 differ only in the sign of their _x_-components, the rotation around the _z_-axis that relates the two cells, i.e. converts
differ only in the sign of their _x_-components, the rotation around the _z_-axis that relates the two cells, i.e. converts 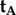 into
into 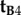 , must be 180°.
, must be 180°.
2.2. Geometric requirements: orientation of magnetoreceptor molecules
Having determined the required cell rotation, we now use a similar analysis to identify and hence exclude those orientations of magnetoreceptor molecules that lead to the same magnetic signals from the two cells.
Theoretical treatments of the anisotropy of the magnetic field effect on flavin-containing radical pairs in cryptochrome have found that the yield of the putative signalling state of the protein approximates to [34,42,47]
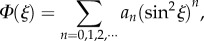 |
2.5 |
|---|
where the an coefficients are constants for a given magnetic field strength and ξ is the angle between the magnetic-field vector and the _z_m-axis of the flavin in the radical pair (figure 1a). Φ(ξ) is cylindrically symmetric around z_m and invariant to inversion of the magnetic field direction (ξ → 180° − ξ), consistent with the axial nature of the avian compass [11]. If the lifetime of the spin-coherence in the radical pair is less than about a microsecond, the terms with n = 0 and n = 1 dominate and Φ(ξ) has a broad, shallow minimum at ξ = 90° (because a_1 < 0, figure 1d). For longer coherence lifetimes, the flavin–tryptophan radical pair has been predicted to show, additionally, a strong, narrow ‘spike’ [47] (figure 1d), that can be modelled by higher order terms (n ≥ 2) in equation (2.5). It has been argued that this feature, which arises from an avoided crossing of the energy levels of the electron-nuclear spin system of the radical pair [47], could afford a precise compass bearing that would be consistent with the ability of migratory songbirds to detect the axis of the magnetic field with an accuracy better than 5° [54–56]
The magnetic signals (equation (2.5)) from cells A and B will only be identical when 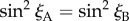 . Writing the two magnetic symmetry axes (related, as above, by a 180° _z_-rotation) as the unit vectors
. Writing the two magnetic symmetry axes (related, as above, by a 180° _z_-rotation) as the unit vectors  and
and 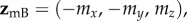 and the magnetic field axis as the unit vector
and the magnetic field axis as the unit vector 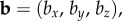 we have:
we have:
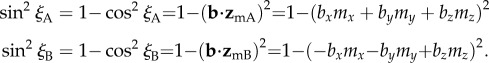 |
2.6 |
|---|
The only way that 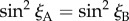 for an arbitrary direction of the magnetic field, b, is either mz = 0 or mx = my = 0, i.e. when the two _z_m-axes are either perpendicular or parallel to the cell rotation axis. In both cases, the two cells would deliver identical magnetic information and the ratio of their outputs would be independent of the magnetic field. In practice, therefore, orientations of the magnetoreceptor molecules that are not too close to either of these extremes should lead to significantly different signals from A and B (see below).
for an arbitrary direction of the magnetic field, b, is either mz = 0 or mx = my = 0, i.e. when the two _z_m-axes are either perpendicular or parallel to the cell rotation axis. In both cases, the two cells would deliver identical magnetic information and the ratio of their outputs would be independent of the magnetic field. In practice, therefore, orientations of the magnetoreceptor molecules that are not too close to either of these extremes should lead to significantly different signals from A and B (see below).
In summary, for axially symmetric receptor cells with the symmetry axis parallel to the incoming light, the ratio of the signals from two adjacent cells will provide pure magnetic information if their orientations are related by a 180° rotation around the cell axis. Within the cell, the cryptochromes should be positioned so that their _z_m-axes are neither approximately parallel nor approximately perpendicular to the cell axis (figure 1c).
2.3. Directional information
In the previous section we derived the conditions under which the ratio of the signals from two adjacent cells in the retina depends only on the orientation of the cells with respect to the axis of the magnetic field. We now explore the directional information conveyed by this ratio.
To keep things simple, we initially consider a single pair of cylindrical cells, A and B, located side-by-side in the retina at a position on the optical axis, i.e. diametrically opposite the pupil (figure 1e). B is rotated relative to A by 180° around the direction of the incoming light, v (which in this case coincides with the optical axis). The cells contain identical magnetoreceptor molecules arranged as in figure 1c with the TDMs (_y_m) aligned parallel to the _x_c-axes of the cells and the magnetic symmetry axes (_z_m) placed in the _y_c_z_c-plane at an angle of 65° to the symmetry axes of the cells (_z_c). The anisotropy of the magnetic signal has the form of equation (2.5) with the coefficients chosen to give a broad background and a prominent spike when the magnetic field is perpendicular to _z_m (ξ = 90°, figure 1d).
We use the Rayleigh sky model for the polarization of the light entering the eye [57–59]. The direction of the electric vector and the degree of polarization vary in a circular fashion around the axis connecting the observer to the sun (figure 1f), with a band of maximum polarization passing north-south across the sky when the sun is on the horizon in the west. This position of the sun was chosen to simulate the twilight conditions under which birds appear to use polarized light cues to calibrate their magnetic compass [60–64]. The maximum degree of polarization was taken as 0.75 (a reasonable value for a clear sunlit sky [65]). This polarization pattern and the arrangement of the cells in figure 1c,e maximize the amount of light absorbed when the eye ‘looks’ horizontally due north. Full details of the calculation are given in the electronic supplementary material.
We calculate the signals from the two cells, 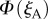 and
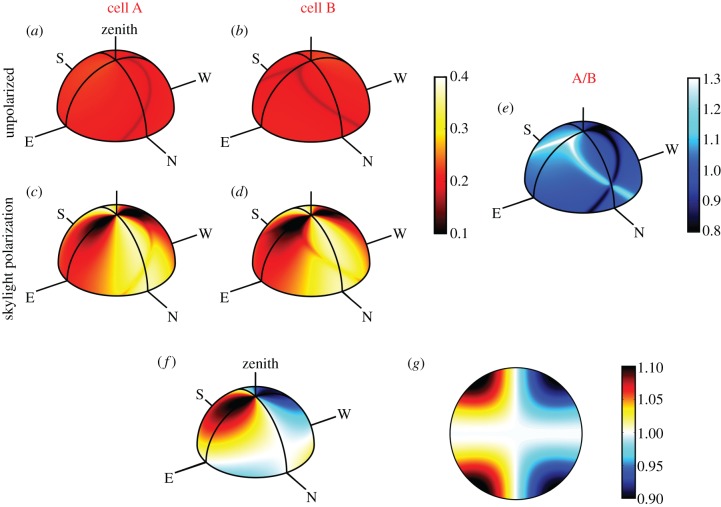
and 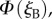 as the eye scans the sky by means of rotations around two perpendicular axes (pitch and yaw, figure 1e). As the line of sight changes, each cell registers the spike whenever the _z_m-axis of its magnetoreceptor molecules is perpendicular to the magnetic field axis, which here points north with an inclination angle of 66° relative to the horizontal. The panels in figure 2a,b show
as the eye scans the sky by means of rotations around two perpendicular axes (pitch and yaw, figure 1e). As the line of sight changes, each cell registers the spike whenever the _z_m-axis of its magnetoreceptor molecules is perpendicular to the magnetic field axis, which here points north with an inclination angle of 66° relative to the horizontal. The panels in figure 2a,b show 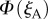 and
and  respectively, projected onto the celestial sphere. The spike in the yield of the signalling state (figure 1d) appears as a narrow band arcing across the sky and the two cells produce mirror-image patterns. The remainder of the magnetic signal (the n = 1 term in equation (2.5), shown as the orange trace in figure 1d) produces a much broader band that is difficult to detect in these figures. The bands associated with the spikes are less apparent for the individual cells when the light is polarized (figure 2c,d) as the magnetic information is partially obscured by the strong variation in light absorption arising from photoselection. However, the ratio of the two signals,
respectively, projected onto the celestial sphere. The spike in the yield of the signalling state (figure 1d) appears as a narrow band arcing across the sky and the two cells produce mirror-image patterns. The remainder of the magnetic signal (the n = 1 term in equation (2.5), shown as the orange trace in figure 1d) produces a much broader band that is difficult to detect in these figures. The bands associated with the spikes are less apparent for the individual cells when the light is polarized (figure 2c,d) as the magnetic information is partially obscured by the strong variation in light absorption arising from photoselection. However, the ratio of the two signals, 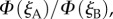 which displays a pattern of two bands, one derived from each cell, is, as expected, identical whether the incoming light is polarized or not (figure 2e). The two bands cross when the orientation of the eye causes the _z_mA and _z_mB axes to be simultaneously perpendicular to the magnetic field, producing a distinct feature that could be used to provide a precise compass bearing. For the geometry used to produce figure 2, this crossing marks magnetic north at an elevation angle equal to the complement of the magnetic inclination, i.e. 24°. A different choice of the orientation of the magnetoreceptor molecules in the cells either puts the crossing point at a different point in the sky or causes the two bands not to cross (a crossing point only occurs when the angle between the vector product
which displays a pattern of two bands, one derived from each cell, is, as expected, identical whether the incoming light is polarized or not (figure 2e). The two bands cross when the orientation of the eye causes the _z_mA and _z_mB axes to be simultaneously perpendicular to the magnetic field, producing a distinct feature that could be used to provide a precise compass bearing. For the geometry used to produce figure 2, this crossing marks magnetic north at an elevation angle equal to the complement of the magnetic inclination, i.e. 24°. A different choice of the orientation of the magnetoreceptor molecules in the cells either puts the crossing point at a different point in the sky or causes the two bands not to cross (a crossing point only occurs when the angle between the vector product 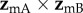 and the _y_c-axis (figure 1c) is smaller than the inclination of the magnetic field, as shown in the electronic supplementary information).
and the _y_c-axis (figure 1c) is smaller than the inclination of the magnetic field, as shown in the electronic supplementary information).
Figure 2.
(a–e) Signals generated by a pair of cells in the centre of the retina as the eye scans the sky. The radical pairs are oriented inside cells A and B according to the Euler angles (α = 90°, β = 65°, γ = 0°) and (α = 270°, β = 65°, γ = 0°), respectively. Light entering the cells is either completely unpolarized, (a) and (b), or is polarized according to the Rayleigh sky model, (c) and (d), with a maximum polarization of 75%. (e) The ratio of the signals from the two cells; this pattern is identical whether the light is polarized or not. The magnetic response is described by equation (2.5) with _a_0 = 0.5, _a_1 = −0.08, _a_128 = −0.01, _a_512 = −0.03, _a_2048 = −0.03 and all other an = 0. The two bands in (c) arise from the spike in figure 1d; their crossing point marks magnetic north at an elevation (24°) equal to the complement of the magnetic inclination. (f,g) Ratio of signals from the two cells when the magnetic response of the radical pairs is described by equation (2.7). (f) The signals generated by a pair of cells in the centre of the retina as the eye scans the sky. (g) The signal received across a hemispherical retina, with the eye looking directly along the magnetic field lines.
Simulations similar to figure 2 suggest that the optimum orientation of the cryptochrome molecule occurs when its magnetic symmetry axis (_z_m) lies in the _y_c_z_c plane of the cell (figure 1c) and makes an angle of 60–70° with respect to the cell's symmetry axis (_z_c). With this geometry, the two bands that arise from the spike (figure 2e) have close to their maximum amplitude and cross at an angle of ca. 90°, arguably affording the clearest indication of the direction of the north-south axis. Moreover, when _z_m lies in the _y_c_z_c plane, the crossing point exists for any magnetic field-inclination.
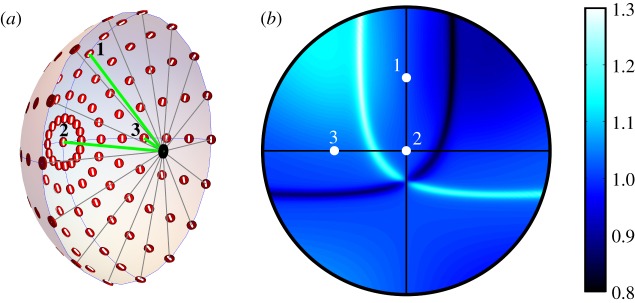
Figure 3 shows the result of a related calculation. Instead of a single pair of magnetoreceptor cells positioned on the optical axis of an eye that scans the sky, we show the signals from an array of paired cells distributed around the retina when the eye looks horizontally to magnetic north. The pattern that results is essentially identical to that in figure 2e.
Figure 3.
(a) Schematic representation of an eye showing representative AB pairs of photoreceptor cells (red discs) distributed around the retina, modelled as a hemisphere with the pupil (black spot) at its centre. The white line through of each of the red discs indicates the direction of the TDM (_y_m axes) in the two cells (figure 1c). Three rays of light are shown entering the eye through the pupil and hitting the retina at points 1, 2 and 3. The photoreceptor cells are arranged with the symmetry (_z_c) axis of each cell pointing towards the pupil and the _x_c axes following the lines of longitude of the sphere, taking the pupil and the centre of the retina as points on the sphere's equatorial plane. (b) An equal-angle projection of the ratio (A/B) of the outputs of the array of cell pairs showing the reference points 1, 2 and 3. The eye looks horizontally to magnetic north. For this simulation, the sun was on the horizon in the west and the maximum polarization was 75%. This is essentially the same pattern as shown in figure 2e.
It is not known whether spin coherence could be preserved long enough in the avian compass to produce a spiked signal of the type modelled above. However, it is still possible to identify a particular bearing (e.g. north) using our proposed receptor set-up with radical pairs that do not produce spikes. Figure 2f,g show an example of this for a radical pair whose singlet yield is described by
 |
2.7 |
|---|
(see orange trace in figure 1d). In these patterns, north can be identified by the point at which the 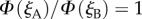 contours cross.
contours cross.
It has been our aim to find conditions under which the ratio of light-induced signals from two adjacent cells is independent of the intensity and polarization of the incident light. However, this is not to say that polarized light no longer has an effect on the output of the compass. If light is polarized parallel to the TDMs of the receptors, more photons will be absorbed than if the light is unpolarized, producing stronger signals from both cells. Although this does not change the size of the A/B ratio (figure 2e), it does lead to an improvement in the signal-to-noise ratio. The example magnetoreceptor orientation used for figure 2 has the TDM oriented such that the chromophore preferentially absorbs the maximally polarized light in the band that stretches across the sky from the northern horizon, to the southern horizon passing through the zenith (figure 1f). In other words, the position of the cross in figure 2e coincides with a direction in which the signal-to-noise should be at a maximum.
3. Discussion
We have discussed the problems associated with a light-dependent magnetoreception mechanism in which magnetic compass information is potentially obscured by variations in the intensity and polarization of the light required to activate the magnetic sensor. The dependence on light intensity can be removed by taking the ratio of the outputs from two neighbouring cells, which receive the same amount of light in the relevant spectral range but generate different magnetic signals [3]. The photoselection effects arising from skylight polarization can also be avoided if the two cells are related by a 180° rotation around the direction of the incoming light. Inside the cells, there are some mild conditions on the allowed orientations of the magnetoreceptor molecules to ensure that the two cells respond differently to the magnetic field in order that the ratio of the two outputs contains magnetic compass information.
Probably the most stringent geometric constraint is that the magnetoreceptor molecules must have a single dominant orientation inside the cells. Previous studies have recognized that a high degree of immobilization and some degree of alignment among the magnetoreceptors is likely to be required for direction sensing [2,34,48,66]. Proposed ways in which this could be achieved [5,27,28,48] include fixing the magnetoreceptor molecules between the stacked membrane discs in the outer segments of photoreceptor cells, binding to quasi-cylindrical membranes in the inner segments of photoreceptor cells, and attachment to the cytoskeleton in retinal ganglion cells. However, it is difficult to see how any of these interactions would preferentially constrain a magnetoreceptor molecule to a single orientation. For example, consider a cryptochrome hypothetically tethered to a rhodopsin molecule embedded in a membrane disc in the outer segment of a photoreceptor cell. Although the rhodopsin orients with its helices spanning the membrane, it is free to rotate around the axis perpendicular to the membrane surface [35,36,48]. A cryptochrome tethered to the rhodopsin would therefore be disordered with respect to rotation around the axis of the cell. Under these circumstances, cells A and B would, on average, give rise to identical magnetic signals. A related point that emerges from these considerations is that if the magnetic directional information is separated from light intensity and polarization effects as proposed here, the suggestion of Lau et al. [34], that photoselection could allow randomly oriented populations of cryptochromes to act as direction sensors, is unlikely to be viable.
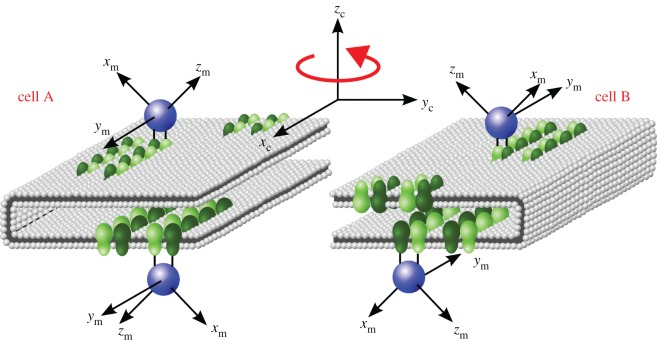
By contrast, the highly ordered ‘tracks’ of rhodopsin dimers recently discovered in the membrane discs of the outer segments of mouse rod photoreceptors [67] could provide the necessary template for orienting magnetoreceptor proteins [3]. The dimer tracks are uniformly aligned parallel to the incisure of the discs which consist of flattened sacs of bilayer membranes, shown schematically in figure 4 [67,68]. Specific binding of a cryptochrome to a rhodopsin dimer would lead to two symmetry-related cryptochrome orientations in each cell. If the geometry of the interaction were as drawn in figure 4, the two orientations would have the same absorption probability for polarized light and the same magnetic field effect (because the _y_m axes are parallel to one another and the _z_m axes are antiparallel). Rotation of the cell and its contents by 180° around its _z_c axis, as shown in figure 4, would not change the absorption probability but would alter the magnetic field effect (because _y_m is still along the ±_x_c axis but _z_m now points in a different direction). It is not essential that the cryptochrome binds directly to the rhodopsin dimer, but it is important that the interaction, whether mediated by other molecules or not, substantially restricts the rotational freedom of the cryptochrome molecules. Currently, not enough is known about the possible interaction partners of cryptochrome to do more than speculate about the possibility of it binding to rhodopsin. However, it is worth noting that, as the interaction could be mediated via linker molecules, there are no specific structural requirements that would make this interaction implausible.
Figure 4.
Schematic picture of the hypothetical interaction of cryptochrome magnetoreceptors (blue spheres) with aligned tracks of rhodopsin dimers (green) embedded in the membrane discs in the outer segments of photoreceptor cells. The figure shows a small section of one of the discs in two neighbouring cells, A and B, related by a 180° rotation around the cell axis, _z_c, which coincides with the direction of the incoming light. The cryptochrome molecule is imagined to bind identically to the top and bottom layers of the discs with the same geometry as in figure 1c. Consequently, binding to rhodopsin tracks in the top and bottom of the membrane discs could fix the cryptochrome molecules into one of two mirror image orientations in each cell. The probability of absorbing a photon is the same for all the cryptochromes in both cells. However, cell A and B will respond differently to an external magnetic field due to the differing orientations of the cryptochrome _z_-axes. Thus, taking the ratio of the outputs from the two cells will give a signal that depends solely on the magnetic field conditions.
In addition to a high degree of ordering of the cryptochromes within the cells, our proposed mechanism requires that the cells occur in pairs with a fixed, well-defined relative orientation of the two partners. Double-cone photoreceptor cells offer one way this could be achieved [3]. These cells are aligned in the retina, contain ordered structures on which cryptochromes could be oriented, and could allow magnetic information to be separated from light intensity and polarization effects as described above. Moreover, cone cells are not visually active at night so that changes in membrane potential generated by magnetic sensors in nocturnal migrants would not have to compete with those generated by visual pigments at night [3]. Given their pencil-shape morphology, it seems plausible that the two components of the double cones could be related by a (180°) rotation around the cell axis as proposed above.
However, some aspects of double-cone morphology could potentially make them unsuitable for our suggested separation mechanism. Firstly, morphological data indicate that, at least in some bird species, just one member of the double cone is associated with a complete oil droplet, while the secondary member either lacks a droplet or possesses a smaller droplet [69]. As these droplets function as filters that narrow the spectrum of light, the assumption that both members of the double cone receive the same light input could be problematic [70,71]. Note that if the oil droplets caused different amounts of light to enter the two cells in a constant ratio, independent of the intensity and polarization of the incident light, this would be equivalent to having different numbers of receptors inside the two cells and would not prevent the separation mechanism from working. If, on the other hand, the fraction of light passing through the oil droplet did depend on its intensity or polarization, the mechanism would break down at the most fundamental level. Second, the model we propose requires that the double cones would need to function as separable units because it is the differential synaptic output that would reflect the magnetic stimuli. However, it appears that at least some double cones are electrically coupled by gap junctions [72] and it is unknown whether these junctions would be functionally ‘open’ during magnetoreception. Neither of these morphological issues has been studied in night-migratory songbirds and, consequently, there are currently too many unknowns to judge whether double cones could really be responsible for magnetoreception, although they are undoubtedly potential candidates. An alternative to comparing the signals from two members of a double cone would be to compare signals coming from two independent neighbouring single or double cones with more similar morphology.
If the magnetoreceptors are indeed inside photoreceptor cells that point at the pupil, as described above, the 180° cell rotation we have proposed is the only way to detect a pure magnetic signal when the incoming light is polarized. However, the precise location of the magnetoreceptors is not known and it is possible that they may occur in other cell types. Conditions for detecting pure magnetic information when the rotation axis of the cell is not parallel to the direction of the incoming light can be derived by extending the above analysis and are outlined in the electronic supplementary material.
The other obvious way to prevent skylight polarization patterns overwhelming the magnetic signal would be to depolarize the light either as it enters the eye or as it enters the cell that contains the magnetoreceptors. This would place far less stringent conditions on the orientation of the magnetoreceptors and their host cells but would seem to be at odds with the fact that birds apparently display polarization-sensitive behaviour, and specifically that they appear to calibrate their magnetic compass using polarized light cues at dusk [60–64]. For the magnetoreceptor to receive depolarized photons without disrupting the birds' ability to respond visually to polarized light, the magnetoreceptor molecules could not be located in the polarization-sensitive photoreceptor cells and would need their own depolarizing filters. In many, but not all, animals polarization detection is mediated by ultraviolet receptors (e.g. some insects [73–75] and fish [76,77]).
Conversely, it is possible that birds do not have a mechanism for separating magnetic and polarized light signals. The ratio of two 90°-rotated cells could be used to remove light intensity, leaving a combined polarization and magnetic signal, which would be in keeping the observation of Muheim et al. [44] that the polarized light cues seem to interact directly with the magnetic compass. However, if this were the case, the bird would need to detect weak magnetic signals in the presence of potentially much larger variations coming from differences in polarization across the sky.
We expect that ultrastructural analyses of the rod and cone photoreceptors in bird retinas using electron microscopy will be capable of testing several aspects of the hypotheses presented here.
Finally, although the results in figure 2 demonstrate that our proposed separation mechanism works for both spike producing and non-spike producing radical pairs, it is clear that the ability to produce a spike offers a great advantage when it comes to identifying a precise magnetic field direction. To determine a direction from figure 2f (no spike) with the same precision as from figure 2e (spike), the bird would need to be over ten times more sensitive to changes in the yield of the signalling state. This high sensitivity requirement would make the compass more susceptible to noise and less able to function under low light conditions.
Supplementary Material
Electronic Supporting Material
Acknowledgements
We are grateful to Dan Nilsson and Michael Land for advice on the alignment of vertebrate photoreceptor cells and to Ben Graves for preliminary calculations.
Data accessibility
This article has no additional data.
Authors' contributions
P.J.H. and H.M. conceived the study. S.W. and P.J.H. designed the study. S.W. performed the study. All three authors discussed the results. S.W. wrote the manuscript with input from P.J.H. and H.M.
Competing interests
We declare we have no competing interests.
Funding
This work was supported by the European Research Council (under the European Union's 7th Framework Programme, FP7/2007-2013/ERC grant agreement no. 340451), the Air Force Office of Scientific Research (Air Force Materiel Command, USAF award no. FA9550-14-1-0095), the Deutsche Forschungsgemeinschaft (GRK 1885) and the Volkswagenstiftung (Lichtenberg Professur).
References
- 1.Schulten K, Swenberg CE, Weller A. 1978. A biomagnetic sensory mechanism based on magnetic field modulated coherent electron spin motion. Z. Phys. Che. 111, 1–5. ( 10.1524/zpch.1978.111.1.001) [DOI] [Google Scholar]
- 2.Ritz T, Adem S, Schulten K. 2000. A model for photoreceptor-based magnetoreception in birds. Biophys. J. 78, 707–718. ( 10.1016/S0006-3495(00)76629-X) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Hore PJ, Mouritsen H. 2016. The radical-pair mechanism of magnetoreception. Annu. Rev. Biophys. 45, 299–344. ( 10.1146/annurev-biophys-032116-094545) [DOI] [PubMed] [Google Scholar]
- 4.Chaves I, et al. 2011. The cryptochromes: blue light photoreceptors in plants and animals. Annu. Rev. Plant Biol. 62, 335–364. ( 10.1146/annurev-arplant-042110-103759) [DOI] [PubMed] [Google Scholar]
- 5.Liedvogel M, Mouritsen H. 2010. Cryptochromes—a potential magnetoreceptor: what do we know and what do we want to know? J. R. Soc. Interface 7, S147–S162. ( 10.1098/rsif.2009.0411.focus) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Biskup T, Schleicher E, Okafuji A, Link G, Hitomi K, Getzoff ED, Weber S. 2009. Direct observation of a photoinduced radical pair in a cryptochrome blue-light photoreceptor. Angew. Chem. Int. Ed. 48, 404–407. ( 10.1002/anie.200803102) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Liedvogel M, Maeda K, Henbest K, Schleicher E, Simon T, Timmel CR, Hore PJ, Mouritsen H. 2007. Chemical magnetoreception: bird cryptochrome 1a is excited by blue light and forms long-lived radical-pairs. PLoS ONE 2, e1106 ( 10.1371/journal.pone.0001106) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Maeda K, et al. 2012. Magnetically sensitive light-induced reactions in cryptochrome are consistent with its proposed role as a magnetoreceptor. Proc. Natl Acad. Sci. USA 109, 4774–4779. ( 10.1073/pnas.1118959109) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Wiltschko W, Wiltschko R. 2001. Light-dependent magnetoreception in birds: the behaviour of European robins, Erithacus rubecula, under monochromatic light of various wavelengths and intensities. J. Exp. Biol. 204, 3295–3302. [DOI] [PubMed] [Google Scholar]
- 10.Wiltschko R, Stapput K, Thalau P, Wiltschko W. 2010. Directional orientation of birds by the magnetic field under different light conditions. J. R. Soc. Interface 7, S163–S177. ( 10.1098/rsif.2009.0367.focus) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Wiltschko W, Wiltschko R. 1972. Magnetic compass of European robins. Science 176, 62–64. ( 10.1126/science.176.4030.62) [DOI] [PubMed] [Google Scholar]
- 12.Sheppard DMW, et al. 2017. Millitesla magnetic field effects on the photocycle of an animal cryptochrome. Sci. Rep. 7, 42228 ( 10.1038/srep42228) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Mouritsen H, Feenders G, Liedvogel M, Wada K, Jarvis ED. 2005. Night-vision brain area in migratory songbirds. Proc. Natl Acad. Sci. USA 102, 8339–8344. ( 10.1073/pnas.0409575102) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Zapka M, et al. 2009. Visual but not trigeminal mediation of magnetic compass information in a migratory bird. Nature 461, 1274–1277. ( 10.1038/nature08528) [DOI] [PubMed] [Google Scholar]
- 15.Ritz T, Thalau P, Phillips JB, Wiltschko R, Wiltschko W. 2004. Resonance effects indicate a radical-pair mechanism for avian magnetic compass. Nature 429, 177–180. ( 10.1038/nature02534) [DOI] [PubMed] [Google Scholar]
- 16.Engels S, et al. 2014. Anthropogenic electromagnetic noise disrupts magnetic compass orientation in a migratory bird. Nature 509, 353–356. ( 10.1038/nature13290) [DOI] [PubMed] [Google Scholar]
- 17.Schwarze S, Schneider N-L, Reichl T, Dreyer D, Lefeldt N, Engels S, Baker N, Hore PJ, Mouritsen H. 2016. Weak broadband electromagnetic fields are more disruptive to magnetic compass orientation in a night-migratory songbird (Erithacus rubecula) than strong narrow-band fields. Front. Behav. Neurosci. 10, 1–13. ( 10.3389/fnbeh.2016.00055) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Ritz T, Wiltschko R, Hore PJ, Rodgers CT, Stapput K, Thalau P, Timmel CR, Wiltschko W. 2009. Magnetic compass of birds is based on a molecule with optimal directional sensitivity. Biophys. J. 96, 3451–3457. ( 10.1016/j.bpj.2008.11.072) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Fedele G, Green EW, Rosato E, Kyriacou CP. 2014. An electromagnetic field disrupts negative geotaxis in Drosophila via a CRY-dependent pathway. Nat. Commun. 5, 4391 ( 10.1038/ncomms5391) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Gegear RJ, Casselman A, Waddell S, Reppert SM. 2008. Cryptochrome mediates light-dependent magnetosensitivity in Drosophila. Nature 454, 1014–1018. ( 10.1038/nature07183) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Gegear RJ, Foley LE, Casselman A, Reppert SM. 2010. Animal cryptochromes mediate magnetoreception by an unconventional photochemical mechanism. Nature 463, 804–807. ( 10.1038/nature08719) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Foley LE, Gegear RJ, Reppert SM. 2011. Human cryptochrome exhibits light-dependent magnetosensitivity. Nat. Commun. 2, 356 ( 10.1038/ncomms1364) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Fedele G, et al. 2014. Genetic analysis of circadian responses to low frequency electromagnetic fields in Drosophila melanogaster. PLoS Genet. 10, e1004804 ( 10.1371/journal.pgen.1004804) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Yoshii T, Ahmad M, Helfrich-Förster C. 2009. Cryptochrome mediates light-dependent magnetosensitivity of _Drosophila_’s circadian clock. PLoS Biol. 7, 0813–0819. ( 10.1371/journal.pbio.1000086) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Marley R, Giachello CNG, Scrutton NS, Baines RA, Jones AR. 2014. Cryptochrome-dependent magnetic field effect on seizure response in Drosophila larvae. Sci. Rep. 4, 5799 ( 10.1038/srep05799) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Giachello CNG, Scrutton NS, Jones AR, Baines RA. 2016. Magnetic fields modulate blue-light-dependent regulation of neuronal firing by cryptochrome. J. Neurosci. 36, 10 742–10 749. ( 10.1523/JNEUROSCI.2140-16.2016) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Bolte P, et al. 2016. Localisation of the putative magnetoreceptive protein cryptochrome 1b in the retinae of migratory birds and homing pigeons. PLoS ONE 11, e0147819 ( 10.1371/journal.pone.0147819) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Mouritsen H, Janssen-Bienhold U, Liedvogel M, Feenders G, Stalleicken J, Dirks P, Weiler R. 2004. Cryptochromes and neuronal-activity markers colocalize in the retina of migratory birds during magnetic orientation. Proc. Natl Acad. Sci. USA 101, 14 294–14 299. ( 10.1073/pnas.0405968101) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Nießner C, Denzau S, Gross JC, Peichl L, Bischof HJ, Fleissner G, Wiltschko W, Wiltschko R. 2011. Avian ultraviolet/violet cones identified as probable magnetoreceptors. PLoS ONE 6, 1–8. ( 10.1371/journal.pone.0020091) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Nießner C, Gross JC, Denzau S, Peichl L, Fleissner G, Wiltschko W, Wiltschko R. 2016. Seasonally changing cryptochrome 1b expression in the retinal ganglion cells of a migrating passerine bird. PLoS ONE 11, e0150377 ( 10.1371/journal.pone.0150377) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Wiltschko R, Ahmad M, Nießner C, Gehring D, Wiltschko W. 2016. Light-dependent magnetoreception in birds: the crucial step occurs in the dark. J. R. Soc. Interface 13, 20151010 ( 10.1098/rsif.2015.1010) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Land MF, Nilsson D-E. 2012. Animal eyes, 2nd edn Oxford, UK: Oxford University Press. [Google Scholar]
- 33.Kram YA, Mantey S, Corbo JC. 2010. Avian cone photoreceptors tile the retina as five independent, self-organizing mosaics. PLoS ONE 5, e8992 ( 10.1371/journal.pone.0008992) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Lau JCS, Rodgers CT, Hore PJ. 2012. Compass magnetoreception in birds arising from photo-induced radical pairs in rotationally disordered cryptochromes. J. R. Soc. Interface 9, 3329–3337. ( 10.1098/rsif.2012.0374) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Cone RA. 1972. Rotational diffusion of rhodopsin in the visual receptor membrane. Nat. New Biol. 236, 39–43. ( 10.1038/newbio236039a0) [DOI] [PubMed] [Google Scholar]
- 36.Cone RA, Poo M. 1974. Lateral diffusion of rhodopsin in the photoreceptor membrane. Nature 247, 438–441. ( 10.1038/252497a0) [DOI] [PubMed] [Google Scholar]
- 37.Roberts NW, Porter ML, Cronin TW. 2011. The molecular basis of mechanisms underlying polarization vision. Phil. Trans. R. Soc. B 366, 627–637. ( 10.1098/rstb.2010.0206) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Tyndall J. 1869. On the blue colour of the sky, the polarization of skylight, and on the polarization of light by cloudy matter generally. Proc. R. Soc. Lond. B 17, 223–233. ( 10.1098/rspl.1868.0033) [DOI] [Google Scholar]
- 39.Gál J, Horváth G, Barta A, Wehner R. 2001. Polarization of the moonlit clear night sky measured by full-sky imaging polarimetry at full Moon: comparison of the polarization of moonlit and sunlit skies. J. Geophys. Res. 106, 22 647–22 653. ( 10.1029/2000JD000085) [DOI] [Google Scholar]
- 40.Cronin TW, Marshall J. 2011. Patterns and properties of polarized light in air and water. Phil. Trans. R. Soc. B 366, 619–626. ( 10.1098/rstb.2010.0201) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Dacke M, Nilsson D-E, Scholtz CH, Byrne M, Warrant EJ. 2003. Insect orientation to polarized moonlight: an African dung beetle uses the moonlit sky to make a swift exit after finding food. Nature 424, 33–34. ( 10.1038/424033a) [DOI] [PubMed] [Google Scholar]
- 42.Lee AA, Lau JCS, Hogben HJ, Biskup T, Kattnig DR, Hore PJ. 2014. Alternative radical pairs for cryptochrome-based magnetoreception. J. R. Soc. Interface 11, 20131063 ( 10.1098/rsif.2013.1063) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Kattnig DR, Solov'yov IA, Hore PJ. 2016. Electron spin relaxation in cryptochrome-based magnetoreception. Phys. Chem. Chem. Phys. 18, 12 443–12 456. ( 10.1039/c5cp06731f) [DOI] [PubMed] [Google Scholar]
- 44.Muheim R, Sjöberg S, Pinzon-Rodriguez A. 2016. Polarized light modulates light-dependent magnetic compass orientation in birds. Proc. Natl Acad. Sci. USA 113, 1654–1659. ( 10.1073/pnas.1513391113) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Eaton WA, Hofrichter J, Makinen MW, Andersen RD, Ludwig ML. 1975. Optical spectra and electronic structure of flavine mononucleotide in flavodoxin crystals. Biochemistry 14, 2146–2151. ( 10.1021/bi00681a016) [DOI] [PubMed] [Google Scholar]
- 46.Climent T, González-Luque R, Merchán M, Serrano-Andrés L. 2006. Theoretical insight into the spectroscopy and photochemistry of isoalloxazine, the flavin core ring. J. Phys. Chem. A 110, 13 584–13 590. ( 10.1021/jp065772h) [DOI] [PubMed] [Google Scholar]
- 47.Hiscock HG, Worster S, Kattnig DR, Steers C, Jin Y, Manolopoulos DE, Mouritsen H, Hore PJ. 2016. The quantum needle of the avian magnetic compass. Proc. Natl Acad. Sci. USA 113, 4634–4639. ( 10.1073/pnas.1600341113) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Solov'yov IA, Mouritsen H, Schulten K. 2010. Acuity of a cryptochrome and vision-based magnetoreception system in birds. Biophys. J. 99, 40–49. ( 10.1016/j.bpj.2010.03.053) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Young RW. 1971. An hypothesis to account for a basic distinction between rods and cones. Vision Res. 11, 1–5. ( 10.1016/0042-6989(71)90201-X) [DOI] [PubMed] [Google Scholar]
- 50.Laties AM. 1969. Histological techniques for study of photoreceptor orientation. Tissue Cell 1, 63–81. ( 10.1016/S0040-8166(69)80006-6) [DOI] [PubMed] [Google Scholar]
- 51.Laties AM, Enoch JM. 1971. An analysis of retinal receptor orientation. Investig. Ophthalmol. Vis. Sci. 10, 69–77. [PubMed] [Google Scholar]
- 52.Smallman HS, MacLeod DIA, Doyle P. 2001. Realignment of cones after cataract removal. Nature 412, 604–605. ( 10.1038/35088126) [DOI] [PubMed] [Google Scholar]
- 53.Westheimer G. 2008. Directional sensitivity of the retina: 75 years of Stiles-Crawford effect. Proc. R. Soc. B 275, 2777–2786. ( 10.1098/rspb.2008.0712) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Lefeldt N, Dreyer D, Schneider N-L, Steenken F, Mouritsen H. 2015. Migratory blackcaps tested in Emlen funnels can orient at 85 degrees but not at 88 degrees magnetic inclination. J. Evol. Biol. 218, 206–211. ( 10.1242/jeb.107235) [DOI] [PubMed] [Google Scholar]
- 55.Åkesson S, Morin J, Muheim R, Ottosson U. 2001. Avian orientation at steep angles of inclination: experiments with migratory white-crowned sparrows at the magnetic North Pole. Proc. R. Soc. Lond. B 268, 1907–1913. ( 10.1098/rspb.2001.1736) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Schwarze S, Steenken F, Thiele N, Kobylkov D, Lefeldt N, Dreyer D, Schneider N-L, Mouritsen H. 2016. Migratory blackcaps can use their magnetic compass at 5 degrees inclination, but are completely random at 0 degrees inclination. Sci. Rep. 6, 33805 ( 10.1038/srep33805) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Strutt HJW. 1871. On the light from the sky, its polarization and colour. Phil. Mag. Ser. 4 41, 107–120. ( 10.1080/14786447108640452) [DOI] [Google Scholar]
- 58.Brines ML, Gould JL. 1982. Skylight polarization patterns and animal orientation. J. Exp. Biol. 96, 69–91. [Google Scholar]
- 59.Pomozi I, Horváth G, Wehner R. 2001. How the clear-sky angle of polarization pattern continues underneath clouds: full-sky measurements and implications for animal orientation. J. Exp. Biol. 204, 2933–2942. [DOI] [PubMed] [Google Scholar]
- 60.Able KP, Able MA. 1993. Daytime calibration of magnetic orientation in a migratory bird requires a view of skylight polarization. Nature 364, 523–525. ( 10.1038/364523a0) [DOI] [Google Scholar]
- 61.Able KP, Able MA. 1995. Manipulations of polarized skylight calibrate magnetic orientation in a migratory bird. J. Comp. Physiol. A 177, 351–356. ( 10.1007/BF00192423) [DOI] [Google Scholar]
- 62.Cochran WW, Mouritsen H, Wikelski M. 2004. Migrating songbirds recalibrate their magnetic compass daily from twilight cues. Science 304, 405–408. ( 10.1126/science.1095844) [DOI] [PubMed] [Google Scholar]
- 63.Muheim R, Phillips JB, Åkesson S. 2006. Polarized light cues underlie compass calibration in migratory songbirds. Science 313, 837–839. ( 10.1126/science.1129709) [DOI] [PubMed] [Google Scholar]
- 64.Muheim R, Åkesson S, Phillips JB. 2007. Magnetic compass of migratory Savannah sparrows is calibrated by skylight polarization at sunrise and sunset. J. Ornithol. 148, 485–494. ( 10.1007/s10336-007-0187-4) [DOI] [Google Scholar]
- 65.Homberg U, Heinze S, Pfeiffer K, Kinoshita M, el Jundi B. 2011. Central neural coding of sky polarization in insects. Phil. Trans. R. Soc. B 366, 680–687. ( 10.1098/rstb.2010.0199) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Hill E, Ritz T. 2010. Can disordered radical pair systems provide a basis for a magnetic compass in animals? J. R. Soc. Interface 7, S265–S271. ( 10.1098/rsif.2009.0378.focus) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Gunkel M, Schöneberg J, Alkhaldi W, Irsen S, Noé F, Kaupp UB, Al-Amoudi A. 2015. Higher-order architecture of rhodopsin in intact photoreceptors and its implication for phototransduction kinetics. Structure 23, 628–638. ( 10.1016/j.str.2015.01.015) [DOI] [PubMed] [Google Scholar]
- 68.Fotiadis D, Jastrzebska B, Philippsen A, Müller DJ, Palczewski K, Engel A. 2006. Structure of the rhodopsin dimer: a working model for G-protein-coupled receptors. Curr. Opin. Struct. Biol. 16, 252–259. ( 10.1016/j.sbi.2006.03.013) [DOI] [PubMed] [Google Scholar]
- 69.Maier EJ, Bowmaker JK. 1993. Colour vision in the passeriform bird, Leiothrix lutea: correlation of visual pigment absorbance and oil droplet transmission with spectral sensitivity. J. Comp. Physiol. A 172, 295–301. ( 10.1007/BF00216611) [DOI] [Google Scholar]
- 70.Hart NS. 2001. The visual ecology of avian photoreceptors. Prog. Retin. Eye Res. 20, 675–703. ( 10.1016/S1350-9462(01)00009-X) [DOI] [PubMed] [Google Scholar]
- 71.Hart NS, Vorobyev M. 2005. Modelling oil droplet absorption spectra and spectral sensitivities of bird cone photoreceptors. J. Comp. Physiol. A Neuroethol. Sens. Neural Behav. Physiol. 191, 381–392. ( 10.1007/s00359-004-0595-3) [DOI] [PubMed] [Google Scholar]
- 72.Smith RL, Nishimura Y, Raviola G. 1985. Interreceptor junction in the double cone of the chicken retina. J. Submicrosc. Cytol. 17, 183–186. [PubMed] [Google Scholar]
- 73.Wehner R. 1989. Neurobiology of polarization vision. Trends Neurosci. 12, 353–359. ( 10.1016/0166-2236(89)90043-X) [DOI] [PubMed] [Google Scholar]
- 74.Taylor GJ, Ribi W, Bech M, Bodey AJ, Rau C, Steuwer A, Warrant EJ, Baird E. 2016. The dual function of orchid bee ocelli as revealed by X-ray microtomography. Curr. Biol. 26, 1319–1324. ( 10.1016/j.cub.2016.03.038) [DOI] [PubMed] [Google Scholar]
- 75.Labhart T, Meyer EP. 1999. Detectors for polarized skylight in insects: a survey of ommatidial specializations in the dorsal rim area of the compound eye. Microsc. Res. Tech. 47, 368–379. ( 10.1002/(SICI)1097-0029(19991215)47:6%3C368::AID-JEMT2%3E3.0.CO;2-Q) [DOI] [PubMed] [Google Scholar]
- 76.Novales FI, Hawryshyn CW, Hárosi FI. 1998. Double-cone internal reflection as a basis for polarization detection in fish. J. Opt. Soc. Am. A 15, 349–358. ( 10.1364/JOSAA.15.000349) [DOI] [PubMed] [Google Scholar]
- 77.Hawryshyn CW. 2000. Ultraviolet polarization vision in fishes: possible mechanisms for coding e-vector. Phil. Trans. R. Soc. Lond. B 355, 1187–1190. ( 10.1098/rstb.2000.0664) [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Electronic Supporting Material
Data Availability Statement
This article has no additional data.