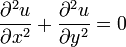Дифференциальное уравнение с частными производными | это... Что такое Дифференциальное уравнение с частными производными? (original) (raw)

Дифференциальное уравнение в частных производных (общеупотребительно сокращение (Д)УЧП, также известны как уравнения математической физики, УМФ) — дифференциальное уравнение, содержащее неизвестные функции нескольких переменных и их частные производные.

Содержание

Введение

Рассмотрим сравнительно простое уравнение в частных производных:

\frac{\partial}{\partial x}u(x,y)=0\, .

Из этого соотношения следует, что значение функции u(x,y) не зависит от x. Следовательно, общее решение уравнения следующее:

u(x,y) = f(y),\,

где f — произвольная функция переменной y. Аналогичное обыкновенное дифференциальное уравнение имеет вид:

\frac{df(y)}{dx}=0\,

и его решение

u(x,y) = c,\,

где c — произвольная константа (независимая от x). Эти два примера показывают, что общее решение обыкновенного дифференциального уравнения содержит неизвестные константы, но общее решение дифференциального уравнения в частных производных содержит произвольные функции. Решение дифференциального уравнения в частных производных, вообще говоря, не единственно. В общем случае на границе рассматриваемой области задаются дополнительные условия. Например, решение выше рассмотренного уравнения (функция f(y)) определяется единственным образом, если u определена на линии x = 0.

История

Первые систематические исследования уравнений в частных производных начал Фурье. Он применил новый метод к решению уравнения струны - метод разделения переменных, позднее получивший его имя.

Классификация

Размерность

Равна количеству независимых переменных. Должна быть не меньше 2 (при 1 получается обыкновенное дифференциальное уравнение).

Линейность

Есть линейные и нелинейные уравнения. Линейное уравнение представимо в виде линейной комбинации производных от неизвестных функций. Коэффициенты при этом могут быть либо постоянными, либо известными функциями.

Линейные уравнения хорошо исследованы, за решение отдельных видов нелинейных уравнений назначены милионные премии (задачи тысячелетия).

Однородность

Уравнение является неоднородным, если есть слагаемое, не зависящее от неизвестных функций.

Порядок

Порядок уравнения определяется максимальным порядком производной. Имеют значение порядки по всем переменным.

Существование и единственность решения

Хотя ответ на вопрос о существовании и единственности решения обыкновенного дифференциального уравнения имеет вполне исчерпывающий ответ (теорема Пикара-Линделёфа), для уравнения в частных производных однозначного ответа на этот вопрос нет. Существует общая теорема (теорема Коши-Ковалевской), которая утверждает, что задача Коши для любого уравнения в частных производных, аналитического относительно неизвестных функций и их производных имеет единственное аналитическое решение. Тем не менее, существуют примеры линейных уравнений в частных производных, коэффициенты которых имеют производные всех порядков и не имеющих решения (Леви (1957)). Даже если решение существует и единственно, оно может иметь нежелательные свойства.

Рассмотрим последовательность задач Коши (зависящую от n) для уравнения Лапласа:

\frac{\part^2 u}{\partial x^2} + \frac{\part^2 u}{\partial y^2}=0,\,

с начальными условиями:

u(x,0) = 0, \,

\frac{\partial u}{\partial y}(x,0) = \frac{\sin n x}{n},\,

где n — целое. Производная от функции u по переменной y равномерно стремится к 0 по x при возрастании n , однако решением уравнения является

u(x,y) = \frac{(\sinh ny)(\sin nx)}{n^2}.\,

Решение стремится к бесконечности, если nx не кратно π для любого ненулевого значения y. задача Коши для уравнения Лапласа называется плохо поставленной или некорректной, так как нет непрерывной зависимости решения от начальных данных.

Примеры

Одномерное уравнение теплопроводности

Уравнение, описывающее распространение тепла в однородном стержне имеет вид

\frac{\partial u}{\partial t} = \alpha \frac{\partial^2 u}{\partial x^2} \,

где u(t,x) — температура, и α — положительная константа, описывающая скорость распространения тепла. Задача Коши ставится следующим образом:

u(0,x)\,= f(x),

где f(x) — произвольная функция.

Уравнение колебания струны

Здесь u(t,x) — смещение струны из положения равновесия, или избыточное давление воздуха в трубе, или магнитуда электромагнитного поля в трубе, а c — скорость распространения волны. Для того, чтобы задачу Коши, в начальный момент времени следует задать смещение и скорость струны в начальный момент времени:

u(0,x) = f(x), \,

u_t(0,x) = g(x), \,

Двумерное уравнение Лапласа

Уравнение Лапласа для неизвестной функции двух переменных имеет вид:

Его решения называются гармоническими функциями.

Связь с аналитическими функциями

Вещественная и мнимая части любой голоморфной функции f комплексной переменной z = z + i y являются сопряжённо гармоническими функциями: они обе удовлетворяют уравнению Лапласа и их градиенты ортогональны. Если _f_=u+iv, то условия Коши-Римана утверждают следующее:

\frac{\partial u}{\partial x} = \frac{\partial v}{\partial y}, \quad \frac{\partial v}{\partial x} = -\frac{\partial u}{\partial y},\,

Складывая и вычитая уравнения друг из друга, получаем:

\frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} = 0, \quad \frac{\partial^2 v}{\partial x^2} + \frac{\partial^2 v}{\partial y^2} = 0. \,

Также можно показать, что любая гармоническая функция является вещественной частью некоторой аналитической функции.

Граничные задачи

Граничные задачи ставятся следующим образом: найти функцию u, которая удовлетворяет уравнению Лапласа во всех внутренних точках области S, а на границе области \partial S — некоторому условию. В зависимости от вида условия различают следующие кравевые задачи:

Решение уравнений математической физики

Существует два вида методов решения данного типа уравнений:

Аналитическое решение

Уравнение колебаний

Рассмотрим задачу о колебаниях струны длины L. Будем считать, что на концах струны функция u(x,t) обращается в ноль:

u(x,t)\big|_{x=0}=u(x,t)\big|_{x=L}=0

В начальный момент времени зададим начальные условия:

u(x,t)\big|_{t=0}=f(x)

\dfrac{\partial u}{\partial t}(x,t)\big|_{t=0}=g(x)

Представим решение в виде:

u(x,t)\,=X(x)T(t)

После подстановки в исходное уравнение колебаний, разделим на произведение X(x)T(t) получаем:

\dfrac{T''(t)}{a^2 T(t)}=\dfrac{X''(x)}{X(x)}

Правая часть этого уравнения зависит от t, левая — от x, следовательно это уравнение может выполняться лишь тогда, когда обе его части равны постоянной величине, которую обозначим через − λ2:

\dfrac{T''(t)}{a^2 T(t)}=\dfrac{X''(x)}{X(x)}=-\lambda^2

Отсюда находим уравнение для X(x):

X''(x)+\lambda^2 X(x)\,=0

Нетривиальные решение этого уравнения при однородных краевых условиях возможны только при \lambda=\dfrac{\pi n}{L} и имеют вид:

X_n(x)\,=sin\left(\dfrac{\pi n x}{L}\right)

Рассмотрим уравнение для отыскания T(t):

T''(t)+a^2\lambda_n^2 T(t)\,=0

Его решение:

T(t)\,=A_n cos\left(\dfrac{a\pi n}{L}t\right)+B_n sin\left(\dfrac{a\pi n}{L}t\right)

Следовательно, каждая функция вида

u(x,t)\,=\left[A_n cos\left(\dfrac{a\pi n}{L}t\right)+B_n sin\left(\dfrac{a\pi n}{L}t\right)\right]sin\left(\dfrac{\pi n x}{L}\right)

является решением волнового уравнения.

Чтобы удовлетворить решение начальным условиям, составим ряд:

u(x,t)\,=\sum\limits_{n=0}^{\infty}\left[A_n cos\left(\dfrac{a\pi n}{L}t\right)+B_n sin\left(\dfrac{a\pi n}{L}t\right)\right]sin\left(\dfrac{\pi n x}{L}\right)

Подстановка в начальные условия даёт:

\sum\limits_{n=0}^{\infty}A_n sin\left(\dfrac{\pi n x}{L}\right)=f(x),\quad \sum\limits_{n=0}^{\infty}\dfrac{a\pi n}{L}B_n sin\left(\dfrac{\pi n x}{L}\right)=g(x)

Последние формулы представляют собой разложение функций f(x) и g(x) в ряд Фурье на отрезке [0,_L_]. Коэфициенты разложений вычисляются по формулам:

A_n=\dfrac{2}{L}\int\limits_{0}^{L}f(x)sin\left(\dfrac{\pi n x}{L}\right)dx,\quad B_n=\dfrac{2}{n\pi a}\int\limits_{0}^{L}g(x)sin\left(\dfrac{\pi n x}{L}\right)dx

Уравнение диффузии

Численное решение

Уравнение колебаний струны

Данный способ решения называется методом конечных дифференциалов. Он достаточно просто реализуем при помощи программирования.

Этот метод основан на определении производной функции y = y(x):

~y'= \lim_{\Delta x \to 0}{\Delta y \over \Delta x} = \lim_{\Delta x \to 0}{{f(x + \Delta x)} - f(x) \over \Delta x}

Если имеется функция u = u(x,t), то частичная производная будет следующая:

~u_x' = {\partial u \over \partial x} = \lim_{\Delta x \to 0}{{u(x + \Delta x, t) - u(x,t)} \over \Delta x}

Так как Δ_x_ мы используем достаточно маленький, знаки пределов можно отбросить. Тогда получим следующие выражения:

~u_x' \approx {{u(x + \Delta x, t) - u(x,t)} \over \Delta x}

~u_t' \approx {{u(x, t + \Delta t) - u(x,t)} \over \Delta t}

Для удобства в дальнейшем примем следующие обозначения:

u(x,t) = u_i^j

u(x + \Delta x,t) = u_{i+1}^j

u(x,t + \Delta t) = u_i^{j+1}

Δ_x_ = h,

Δ_t_ = τ

Тогда предыдущие выражения можно записать так: u_x' \approx {{u_{i+1}^j - u_i^j} \over h}, u_t' \approx {{u_i^{j+1} - u_i^j} \over \tau}

Эти выражения называют правыми дифференциалами. Их можно записать и по-другому: u_x' \approx {{u_i^j - u_{i-1}^j} \over h}, u_t' \approx {{u_i^j - u_i^{j-1}} \over \tau} — это левые дифференциалы.

Просуммировав оба выражения получим следующее:

2 u_x' \approx {{u_i^j - u_{i-1}^j + u_{i+1}^j - u_i^j} \over h}

2 u_t' \approx {{u_i^j - u_i^{j-1} + u_i^{j+1} - u_i^j} \over \tau}

из которых следует:

u_x' \approx {{u_{i+1}^j - u_{i-1}^j} \over 2h}

u_t' \approx {{u_i^{j+1} - u_i^{j-1}} \over 2\tau}

Аналогично можно получить и дифференциалы второго порядка:

u_{xx}^{''} = {{\partial ^2u} \over {\partial x^2}} \approx {{u_{i-1}^j - 2u_i^j + u_{i+1}^j} \over h^2}

u_{tt}^{''} = {{\partial ^2u} \over {\partial t^2}} \approx {{u_i^{j-1} - 2u_i^j + u_i^{j+1}} \over \tau ^2}

Уравнение колебаний струны записывается в такой форме: \frac{\partial^2 u}{\partial t^2} = a^2 \frac{\partial^2 u}{\partial x^2}.

Дополнительные условия задаются в виде: u | x = 0 = _f_1(t), u | x = l = _f_2(t), u | t = 0 = _g_1(x), u t | t = 0 = _g_2(x),

где _f_1(t) и _f_2(t) — позиции концов (креплений) струны во времени,

а _g_1(x) и _g_2(x) — начальное состояние и скорость струны из которой мы можем получить состояние струны в следующий момент времени по формуле

Сетка значений функции

u_i^{j+1} = \tau \cdot g_2(x) + u_i^j.

В вычислениях используют дискретизацию струны (разделяют её на одинаковые интервалы, длина которых h (см.рис).

Значения функции остальным x и t можно вычислить из уравнения колебаний струны:

\frac{\partial^2 u}{\partial t^2} = a^2 \frac{\partial^2 u}{\partial x^2}

{{\partial ^2u} \over {\partial t^2}} = {{u_i^{j+1} - 2u_i^j + u_i^{j-1}} \over \tau ^2}

{{\partial ^2u} \over {\partial x^2}} = {{u_{i+1}^j - 2u_i^j + u_{i-1}^j} \over h^2}

{{u_i^{j+1} - 2u_i^j + u_i^{j-1}} \over \tau ^2} = a^2{{u_{i+1}^j - 2u_i^j + u_{i-1}^j} \over h^2}

u_i^{j+1} = {{\tau ^2 a^2 \over h^2}} \left( u_{i+1}^j - 2u_i^j + u_{i-1}^j \right) + 2u_i^j - u_i^{j-1}

Таким образом, мы получили схему, по которой можно получить значения функции для любых x и t, используя значения функции при предыдущих x и t. Схематично это можно представить так:

Нахождение пятой точки по четерём известным

Этот метод даёт приближённый ответ, степень точности Θ(τ2 + _h_2). Для достаточно точных результатов необходимо использовать интервалы h < 0.1 и \tau \le {h^2 \over 2}.

Уравнение диффузии

См. также

Ссылки

Wikimedia Foundation.2010.