DLMF: Chapter 5 Gamma Function (original) (raw)

R. A. Askey Department of Mathematics, University of Wisconsin, Madison, Wisconsin. R. Roy Department of Mathematics and Computer Science, Beloit College, Beloit, Wisconsin.

ⓘ

Acknowledgements:

This chapter is based in part onAbramowitz and Stegun (1964, Chapter 6) by P. J. Davis.

Notes:

The main references used in writing this chapter areAndrews et al. (1999),Carlson (1977b),Erdélyi et al. (1953a),Nielsen (1906a),Olver (1997b),Paris and Kaminski (2001),Temme (1996b), andWhittaker and Watson (1927).

Referenced by:

New Associate Editors for the DLMF,Profile Gergő Nemes,Profile Richard A. Askey,Profile Ranjan Roy,Profile Simon Ruijsenaars,§ ‣ Chapter Authors,§ ‣ Chapter Authors,§ ‣ Associate Editors,§ ‣ Associate Editors,Version 1.2.0 (March 27, 2024),§ ‣ Software Cross Index

Permalink:

http://dlmf.nist.gov/5

• Notation

  1. 5.1 Special Notation

• Properties

  1. 5.2 Definitions
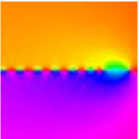
  2. 5.3 Graphics
  3. 5.4 Special Values and Extrema
  4. 5.5 Functional Relations
  5. 5.6 Inequalities
  6. 5.7 Series Expansions
  7. 5.8 Infinite Products
  8. 5.9 Integral Representations
  9. 5.10 Continued Fractions
  10. 5.11 Asymptotic Expansions
  11. 5.12 Beta Function
  12. 5.13 Integrals
  13. 5.14 Multidimensional Integrals
  14. 5.15 Polygamma Functions
  15. 5.16 Sums
  16. 5.17 Barnes’ G-Function (Double Gamma Function)
  17. 5.18 q-Gamma and q-Beta Functions

• Applications

  1. 5.19 Mathematical Applications
  2. 5.20 Physical Applications

• Computation

  1. 5.21 Methods of Computation
  2. 5.22 Tables
  3. 5.23 Approximations
  4. 5.24 Software